离散数学-命题逻辑学习笔记-1

/***********************************************MATH******************************************************/

离散数学：研究的对象是有限个或可数的离散量。

逻辑学：辩证逻辑和形式逻辑。思维的形式结构包含了概念、判断、推理之间的结构和联系。

数理逻辑：用数学方法研究推理的规律。

一、命题逻辑：

1、命题

具有确切真值的陈述句为命题。（不可以是疑问句、祈使句、感叹句等）其中所谓真值并不是只有真，

真值指的是可以是“真”或者“假”。正是对应计算机中的0和1，true和false。示例如下：

“今天下雪”--------》是一个陈述命题；
“4+8=12"---------->是命题，并且很明显是一个真命题；
"x+y>6"----------->不是命题,x和y是自由变量，不是命题是一个条件表达式；
"太棒了！"--------->不是命题，非陈述句;

1.1\命题类型

命题可以分为简单命题和复合命题。

简单命题是不可拆分的命题，相反复合命题就是由简单命题复合而成。简单命题之间通过关联词或者标点符号来连接。

1.2\命题联结词

命题联结词在数理逻辑中可以看作逻辑运算符。常用联结词有非¬（¬P指的是P不成立）、合取∧（P∧Q指的是命题P且Q）、析取∨（P∨Q指的是P或者Q）、蕴含→（P→Q指的是如果P，那么Q）、等价↔（P↔Q指的是P当且仅当Q）。

注意：蕴含→有多种叫法，P→Q，那么P是Q的充分条件，Q是P的必要条件。

\一般约定\

根据结合力强弱顺序，否定、合取、析取、蕴含、等价。按照约定的式子不需要括号，否则需要加括号进行运算

\示例\

1、他既有理论知识又有实际经验
P：他有理论知识
Q：他有实际经验
P^Q
2、当且仅当明天不下雪并且明天不下雨，我才去科大。
P:明天下雪
Q：明天下雨
R：我去科大
（¬P ∧ ¬Q ）↔ R
3、如果我上街了，我就去科大看看，除非我很累。
P：我上街了。

Q：我去科大看看。

R：我很累。
(P∧¬R)→Q

否定¬常用“非”、“没有”、“不”，合取∧常用“并且”、“和”，析取常用“或者”、“或”、“近似或”等等，蕴含常用“如果，，，那么，，，”、“，，仅当，，，”，等价常用“当且仅当”。

1.3\命题公式

常值命题：具有确切值的命题。

命题变量：没有赋予具体内容的原子命题。

命题公式：(1) 命题变元本身是一个公式； (2) 如果P是公式，则¬P也是公式； (3) 如果P，Q是公式，则P∧Q﹑ P∨Q﹑ P→Q﹑ P↔Q也是公式； (4) 命题公式(Prepositional Formula)是仅由有限步 使用规则(1)~(3)后产生的结果。公式常用符号G﹑ H…等表示。

注意：并不是说由命题变量和联结词组成就是命题公式

(¬ P∧Q)是命题公式，(P →Q )∧¬ Q)就不是。

命题公式也叫合式，合式没有真值，只有赋予其具体的内容才能得出真值。

1.3.1、合成公式的层次

（1）若A是命题变元，那么它就是0层

（2）A是n+1层，只需要满足下列之一即可：

1、A=¬B，B为n层；
2、A=B^C 或者 A=B∨B 或者 A=B→C 或者 A=B↔C n=max(i,j)其中i,j是B的层次、C的层次。

1.3.2、常用五个联结词的真值表

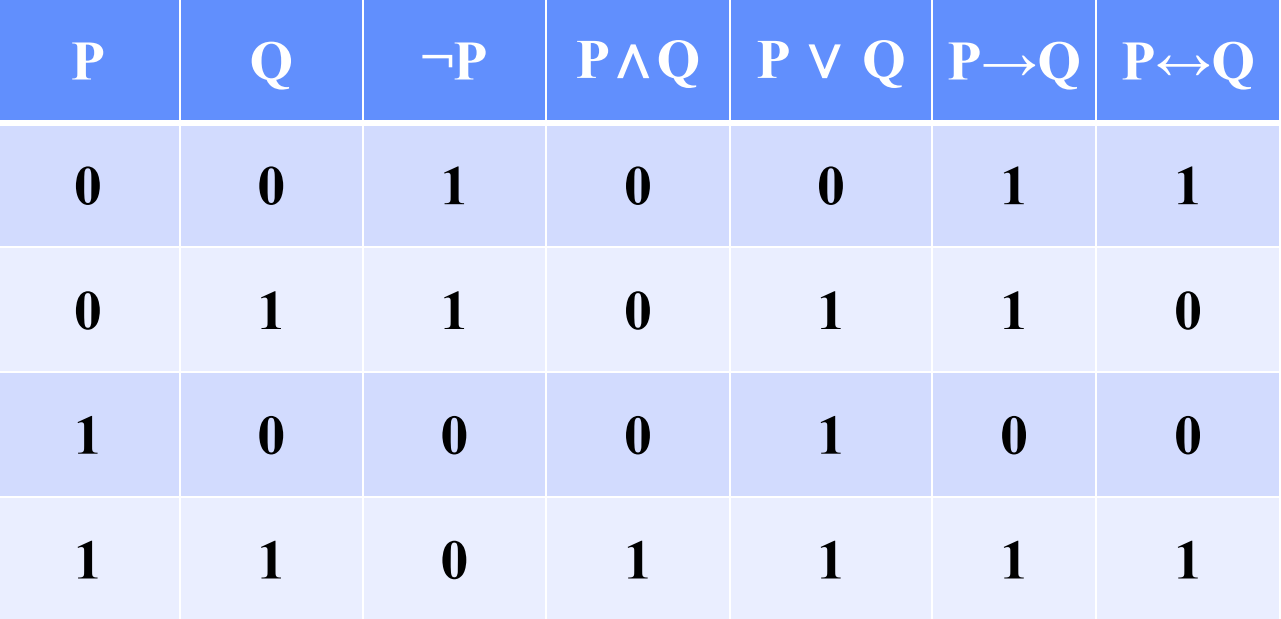
注意：蕴含P → Q（如果 P，那么 Q）仅在 P 为真且 Q 为假 时为假，其余情况为真。

等价P ↔ Q（P 当且仅当 Q）在 P 和 Q 真值相同 时为真。

/********************************************continue*******************************************************/