CMU 11-785 L16 Connectionist Temporal Classification

Sequence to sequence

• Sequence goes in, sequence comes out
• No notion of “time synchrony” between input and output
  • May even nots maintain order of symbols (from one language to another)

With order synchrony

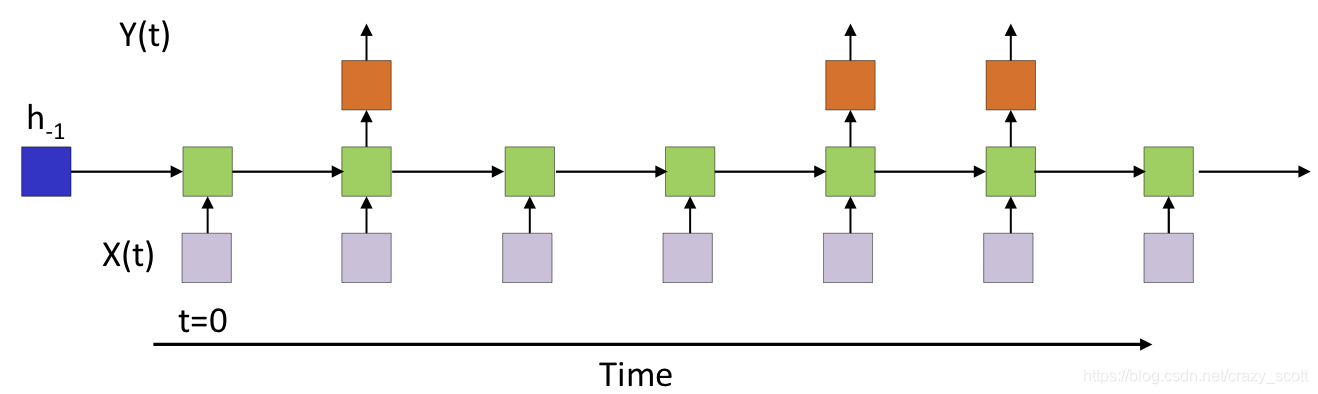
• The input and output sequences happen in the same order
  • Although they may be time asynchronous
  • E.g. Speech recognition
    • The input speech corresponds to the phoneme sequence output
• Question
  • How do we know when to output symbols
  • In fact, the network produces outputs at every time
  • Which of these are the real outputs?

Option 1

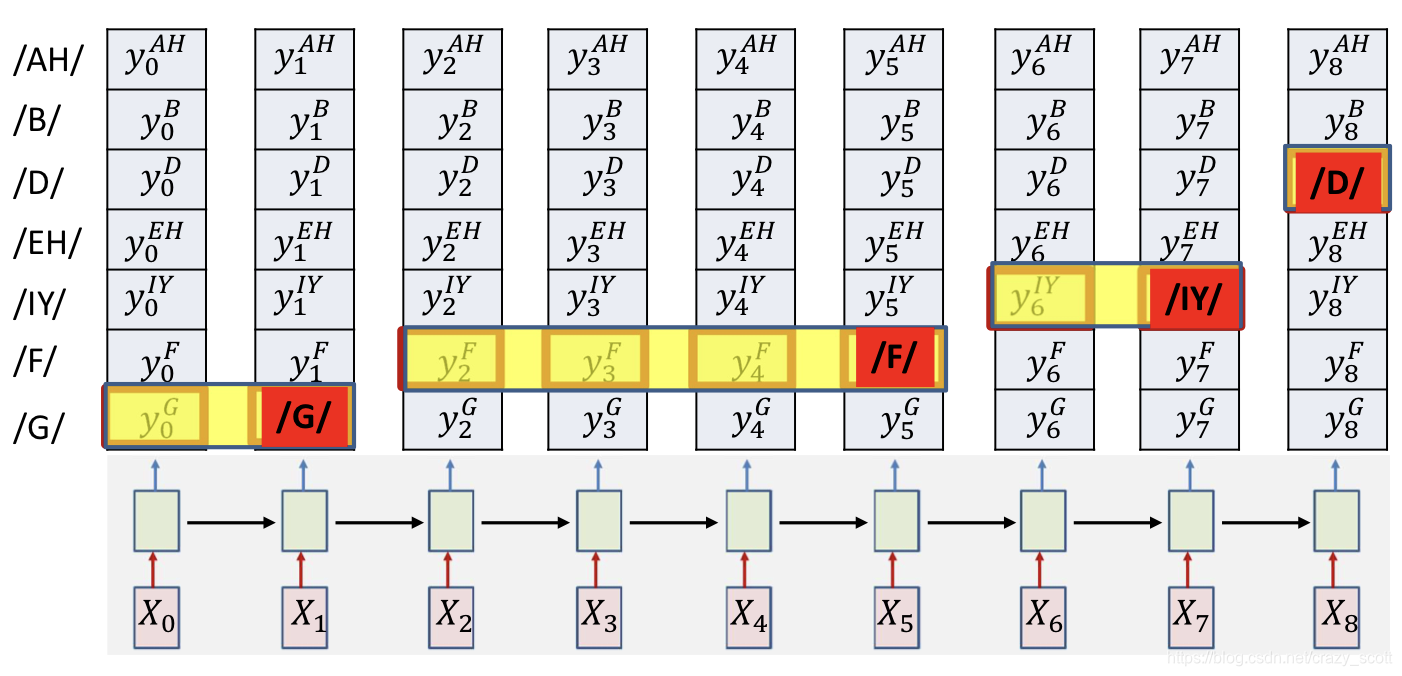
• Simply select the most probable symbol at each time
• Merge adjacent repeated symbols, and place the actual emission of the symbol in the final instant
• Problem
  • Cannot distinguish between an extended symbol and repetitions of the symbol
  • Resulting sequence may be meaningless

Option 2

• Impose external constraints on what sequences are allowed
  • E.g. only allow sequences corresponding to dictionary words

Decoding

• The process of obtaining an output from the network

• Time-synchronous & order-synchronous sequence

  • aaabbbbbbccc => abc (probility 0.5)
    aabbbbbbbccc => abc (probility 0.001)
    cccddddddeee => cde (probility 0.4)
    cccddddeeeee => cde (probility 0.4)
    

  • So abc is the most likely time-synchronous output sequence
  • But cde is the the most likely order-synchronous sequence

• Option 2 is in fact a suboptimal decode that actually finds the most likely time-synchronous output sequence

• The “merging” heuristics do not guarantee optimal order-synchronous sequences

No timing information provided

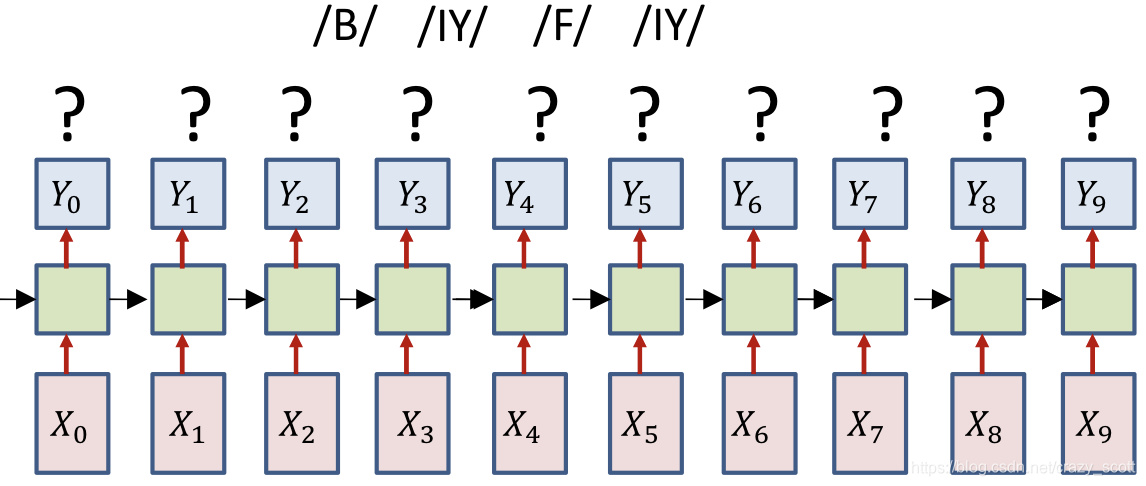
• Only the sequence of output symbols is provided for the training data
  • But no indication of which one occurs where

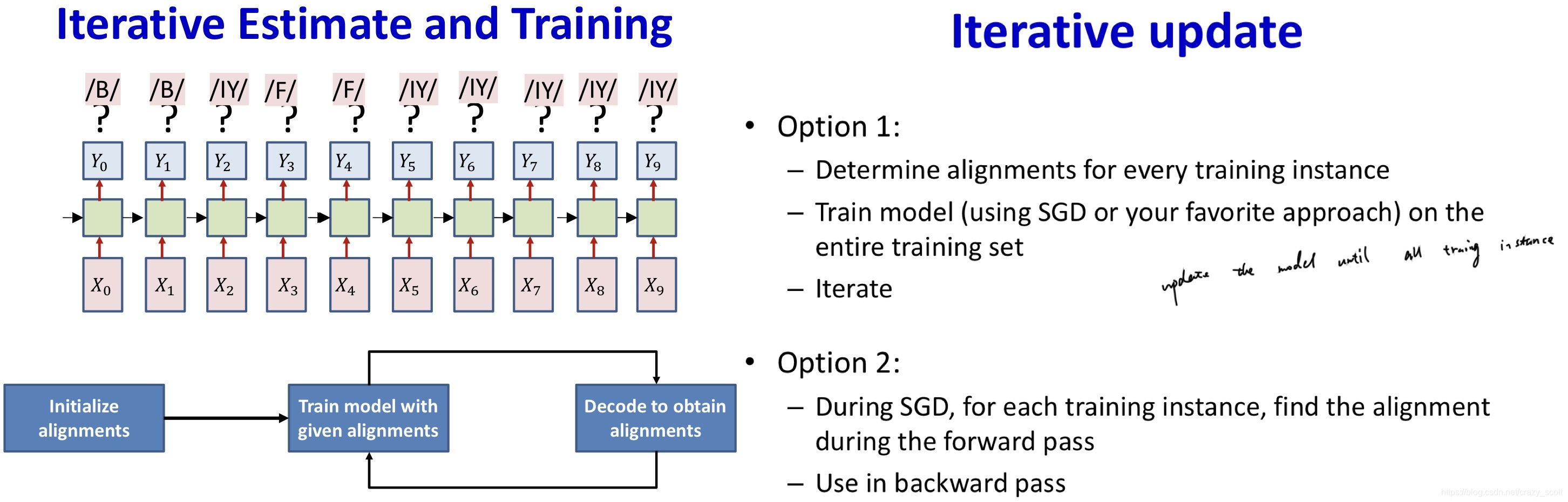
Guess the alignment

• Initialize
  • Assign an initial alignment
  • Either randomly, based on some heuristic, or any other rationale
• Iterate
  • Train the network using the current alignment
  • Reestimate the alignment for each training instance

Constraining the alignment

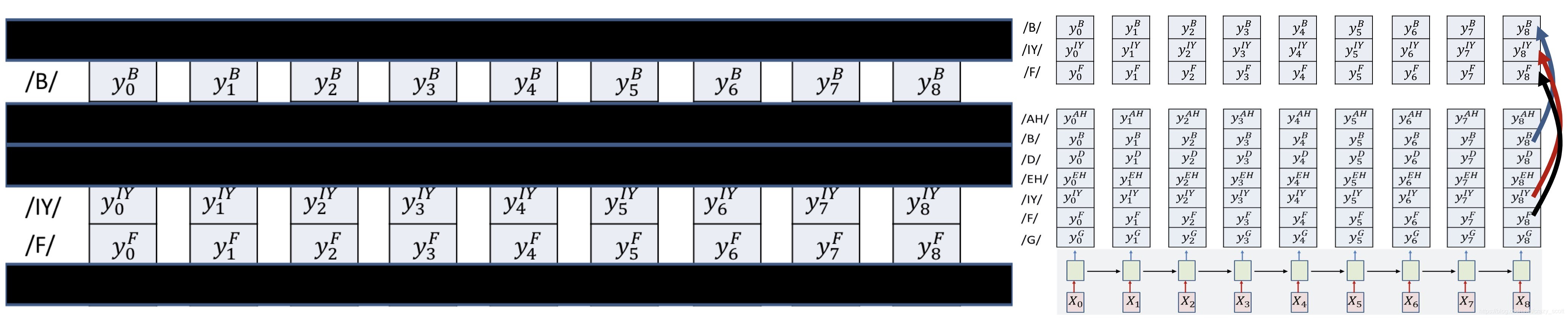
• Try 1
  • Block out all rows that do not include symbols from the target sequence
  • E.g. Block out rows that are not /B/ /IY/ or /F/
• Only decode on reduced grid
  • We are now assured that only the appropriate symbols will be hypothesized
• But this still doesn’t assure that the decode sequence correctly expands the target symbol sequence
  • Order variance
• Try 2
  • Explicitly arrange the constructed table
  • Arrange the constructed table so that from top to bottom it has the exact sequence of symbols required
    • If a symbol occurs multiple times, we repeat the row in the appropriate location

• Constrain that the first symbol in the decode must be the top left block

  • The last symbol must be the bottom right
  • The rest of the symbols must follow a sequence that monotonically travels down from top left to bottom right
  • This guarantees that the sequence is an expansion of the target sequence

• Compose a graph such that every path in the graph from source to sink represents a valid alignment

  • The “score” of a path is the product of the probabilities of all nodes along the path
  • Find the most probable path from source to sink using any dynamic programming algorithm (viterbi algorithm)

Viterbi algorithm

• Main idea

  • The best path to any node must be an extension of the best path to one of its parent nodes

• Dynamically track the best path (and the score of the best path) from the source node to every node in the graph

  • At each node, keep track of
    • The best incoming parent edge (BP)
    • The score of the best path from the source to the node through this best parent edge (Bscr)

• Process
  

• Algorithm
  

Gradients

$$DIV=\sum _{t}Xent\left(Y_t,symbo{l}_t^{bestpath}\right)=-\sum _t\log Y\left(t,symbo{l}_t^{bestpath}\right)$$

• The gradient w.r.t the -th output vector $Y_t$
  $${\nabla }_{Y_t}DIV=[00\cdot \cdot \cdot \frac{-1}{Y(t,symbo{l}_t^{bestpath})}0\cdot \cdot \cdot 0]$$

• Problem

  • Approach heavily dependent on initial alignment
  • Prone to poor local optima
    • Because we commit to the single “best” estimated alignment
    • This can be way off, particularly in early iterations, or if the model is poorly initialized

• Alternate view

  • There is a probability distribution over alignments of the target Symbol sequence (to the input)
  • Selecting a single alignment is the same as drawing a single sample from it

• Instead of only selecting the most likely alignment, use the statistical expectation over all possible alignments

  • $$DIV=E\left[-\sum _t\log Y\left(t,s_t\right)\right]$$

  • Use the entire distribution of alignments

  • This will mitigate the issue of suboptimal selection of alignment

• Using the linearity of expectation

  • $$DIV=-\sum _{t}E\left[\log Y\left(t,s_t\right)\right]$$

  • $$DIV=-\sum _t\sum _{S\in S_1\dots S_K}P\left(s_t=S|\mathbf{S},\mathbf{X}\right)\log Y\left(t,s_t=S\right)$$

A posteriori probabilities of symbols

• $P(s_t=S|\mathbf{S},\mathbf{X})$ is the probability of seeing the specific symbol s s