CMU 11-785 L03 Learning the network-优快云博客

本文探讨了神经网络的基本概念，包括偏置项的作用、权重更新规则及最小化经验风险的策略。通过解析感知器算法和多层感知器，阐述了如何通过训练数据集调整网络参数，实现对复杂问题的解决。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Preliminary

The bias can also be viewed as the weight of another input component that is always set to 1
$z=∑iwixiz=\sum_{i} w_{i} x_{i}$
What we learn: The …parameters… of the network
Learning the network: Determining the values of these parameters such that the network computes the desired function
How to learn a network?
- $W^=argmin⁡W∫Xdiv⁡(f(X;W),g(X))d \widehat{\boldsymbol{W}}=\underset{W}{\operatorname{argmin}} \int_{X} \operatorname{div}(f(X ; W), g(X)) d$
- div() is a divergence function thet goes to zero when $f (X; W) = g (X)$
But in practice $g (x)$ will not have such specification
- Sample $g (x)$ : just gather training data

Learning

Simple perceptron

do For $i = 1.. N_{train}$

$O(x_i) = sign(W^TX_i)$

if $O(xi)≠yiO(x_i) \neq y_i$

$W = W+Y_iX_i$

until no more classification errors

A more complex problem

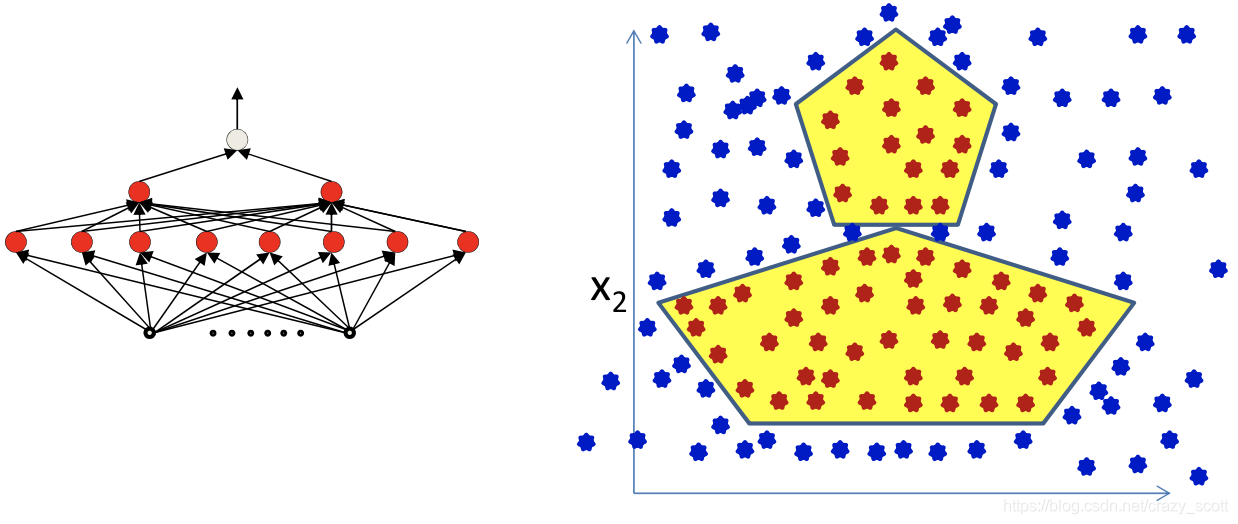
在这里插入图片描述

This can be perfectly represented using an MLP
But perveptron algorithm require linearly separated labels to be learned in lower-level neurons
- An exponential search over inputs
So we need differentiable function to compute the change in the output for …small… changes in either the input or the weights

Empirical Risk Minimization

Assuming $X$ is a random variable:
$W^=argmin⁡W∫Xdiv⁡(f(X;W),g(X))P(X)dX=argmin⁡WE[div⁡(f(X;W),g(X))] \begin{aligned} \widehat{\boldsymbol{W}}=& \underset{W}{\operatorname{argmin}} \int_{X} \operatorname{div}(f(X ; W), g(X)) P(X) d X \\ &=\underset{W}{\operatorname{argmin}} E[\operatorname{div}(f(X ; W), g(X))] \end{aligned}$
Sample $g (X)$ , where $di=g(Xi)+noised_{i}=g\left(X_{i}\right)+ noise$ , estimate function from the samples

The empirical estimate of the expected error is the average error over the samples
$E[\operatorname{div}(f(X ; W), g(X))] \approx \frac{1}{N} \sum_{i=1}^{N} \operatorname{div}\left(f\left(X_{i} ; W\right), d_{i}\right)$

Empirical average error (Empirical Risk) on all training data
$\operatorname{Loss}(W)=\frac{1}{N} \sum_{i} \operatorname{div}\left(f\left(X_{i} ; W\right), d_{i}\right)$

Estimate the parameters to minimize the empirical estimate of expected error
$W^=argmin⁡WLoss⁡(W) \widehat{\boldsymbol{W}}=\underset{W}{\operatorname{argmin}} \operatorname{Loss}(W)$

Problem statement

Given a training set of input-output pairs

$\left(\boldsymbol{X}_{1}, \boldsymbol{d}_{1}\right),\left(\boldsymbol{X}_{2}, \boldsymbol{d}_{2}\right), \ldots,\left(\boldsymbol{X}_{N}, \boldsymbol{d}_{N}\right)$