CMU 11-785 L12 Back propagation through a CNN_div =鈭掆垏-优快云博客

本文深入探讨了卷积神经网络（CNN）的工作原理，包括卷积层、池化层、反卷积层的计算过程，以及如何通过反向传播进行权重更新。特别介绍了在训练过程中如何处理Max-Pooling层的导数，以及使用平均池化和转置卷积的技巧。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Convolution

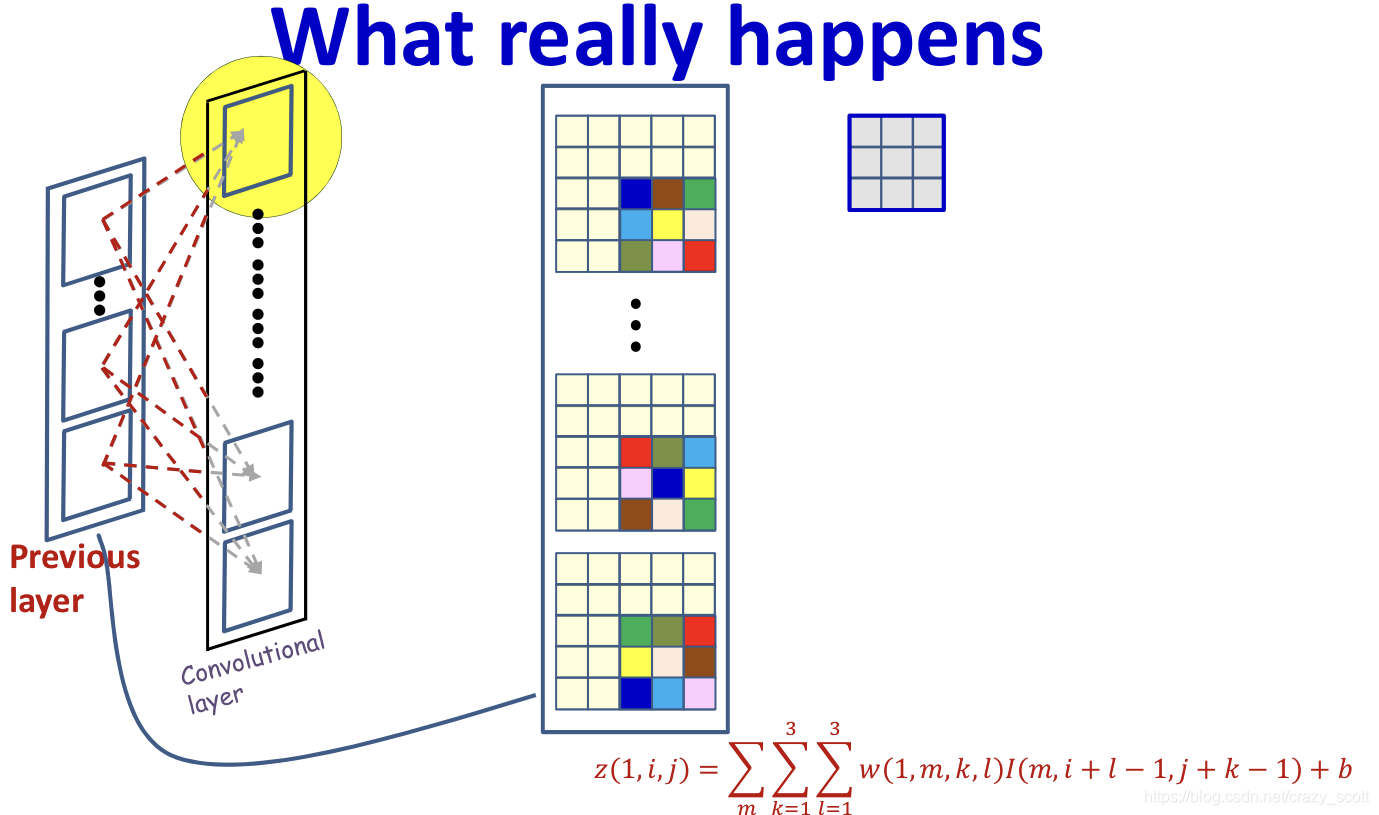
在这里插入图片描述

Each position in $z$ consists of convolution result in previous map

在这里插入图片描述

Way for shrinking the maps
- Stride greater than 1
- Downsampling (not necessary)
  - Typically performed with strides > 1
Pooling
- Maxpooling
  - Note: keep tracking of location of max (needed while back prop)
- Mean pooling

Learning the CNN

Training is as in the case of the regular MLP
- The only difference is in the structure of the network
Define a divergence between the desired output and true output of the network in response to any input
Network parameters are trained through variants of gradient descent
Gradients are computed through backpropagation

在这里插入图片描述

Final flat layers

Backpropagation continues in the usual manner until the computation of the derivative of the divergence
Recall in Backpropagation
- Step 1: compute $\frac{\partial Div}{\partial z^{n}}$ 、 $\frac{\partial Div}{\partial y^{n}}$
- Step 2: compute $\frac{\partial Div}{\partial w^{n}}$ according to step 1

Convolutional layer

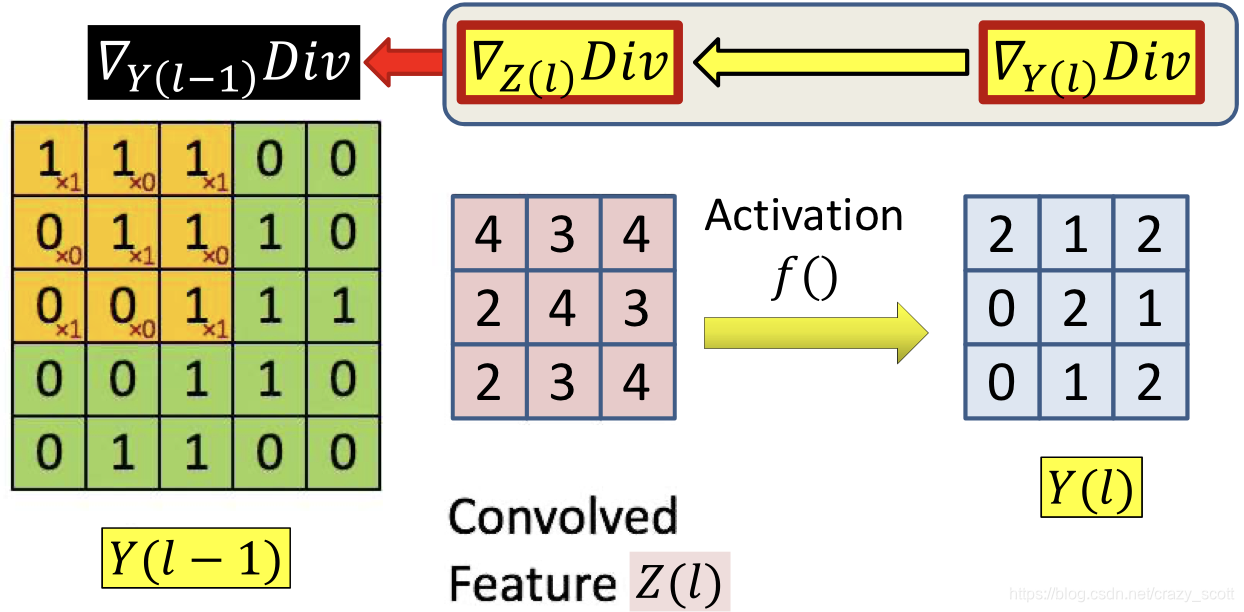
在这里插入图片描述

Computing $\nabla_{Z(l)} D i v$

$\frac{d D i v}{d z(l, m, x, y)}=\frac{d D i v}{d Y(l, m, x, y)} f^{\prime}(z(l, m, x, y))$
Simple compont-wise computation

Computing $\nabla_{Y(l-1)} D i v$

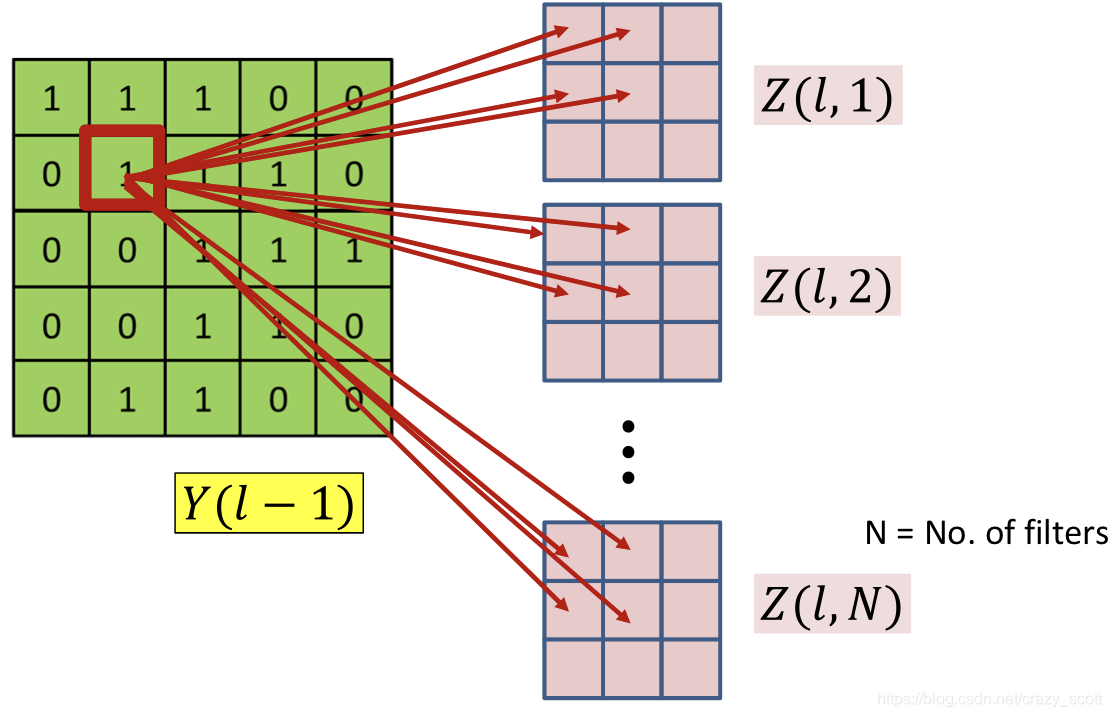
在这里插入图片描述

Each $Y (l - 1, m, x, y)$ affects several $z(l,n,x\prime,y\prime)$ terms for every $n$ (map)
- Through $w_l(m,n,x-x\prime,y-y\prime)$
- Affects terms in all $l^{th}$ layer maps
- All of them contribute to the derivative of the divergence $Y (l - 1, m, x, y)$
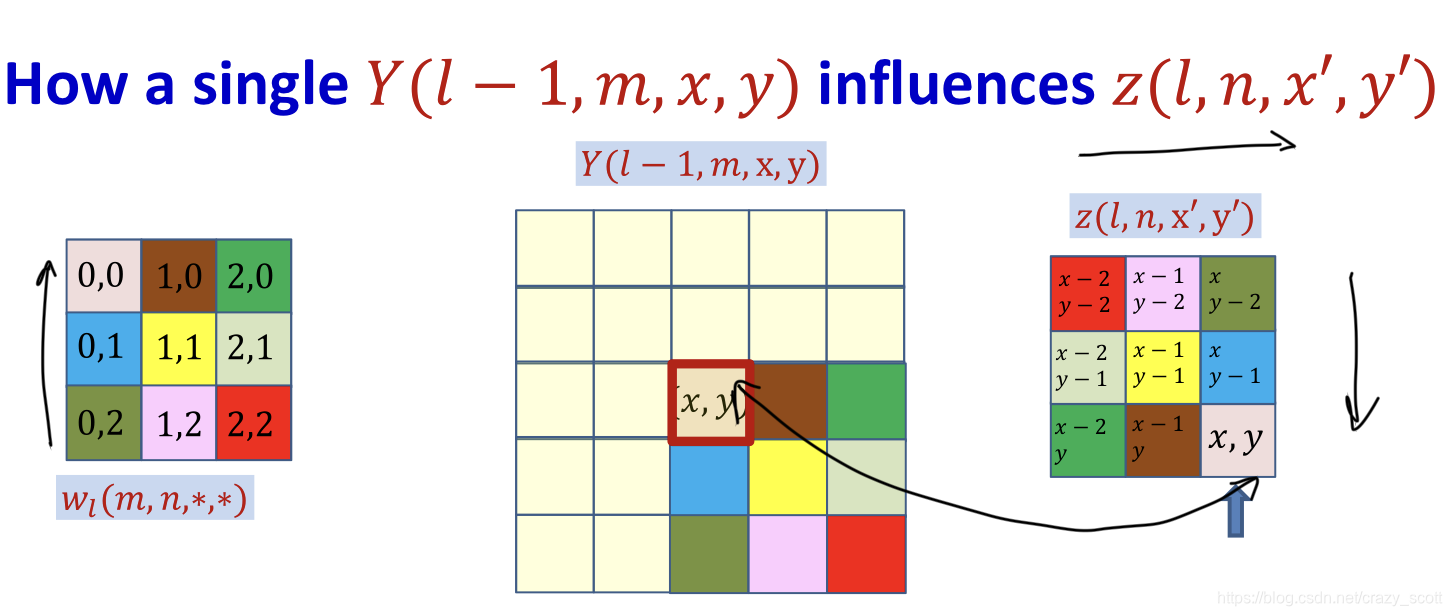
Derivative w.r.t a specific $y$ term

$\frac{d D i v}{d Y(l-1, m, x, y)}=\sum_{n} \sum_{x^{\prime}, y^{\prime}} \frac{d D i v}{d z\left(l, n, x^{\prime}, y^{\prime}\right)} \frac{d z\left(l, n, x^{\prime}, y^{\prime}\right)}{d Y(l-1, m, x, y)}$

$\frac{d D i v}{d Y(l-1, m, x, y)}=\sum_{n} \sum_{x \prime, y^{\prime}} \frac{d D i v}{d z\left(l, n, x^{\prime}, y^{\prime}\right)} w_{l}\left(m, n, x-x^{\prime}, y-y^{\prime}\right)$

Computing $\nabla_{w(l)} D i v$

Each weight $w_l(m,n,x\prime,y\prime)$ also affects several $z (l, n, x, y)$ term for every $n$
- Affects terms in only one $Z$ map (the nth map)
- All entries in the map contribute to the derivative of the divergence w.r.t. $w_l(m,n,x\prime,y\prime)$
Derivative w.r.t a specific $w$ term

$\frac{d D i v}{d w_{l}(m, n, x, y)}=\sum_{x^{\prime}, y^{\prime}} \frac{d D i v}{d z\left(l, n, x^{\prime}, y^{\prime}\right)} \frac{d z\left(l, n, x^{\prime}, y^{\prime}\right)}{d w_{l}(m, n, x, y)}$

$\frac{d D i v}{d w_{l}(m, n, x, y)}=\sum_{x \prime, y^{\prime}} \frac{d D i v}{d z\left(l, n, x^{\prime}, y^{\prime}\right)} Y\left(l-1, m, x^{\prime}+x, y^{\prime}+y\right)$

Summary

在这里插入图片描述

In practice

$\frac{d D i v}{d Y(l-1, m, x, y)}=\sum_{n} \sum_{x \prime, y^{\prime}} \frac{d D i v}{d z\left(l, n, x^{\prime}, y^{\prime}\right)} w_{l}\left(m, n, x-x^{\prime}, y-y^{\prime}\right)$

在这里插入图片描述

This is a convolution, with defferent order
- Use mirror image to do normal convolution (flip up down / flip left right)

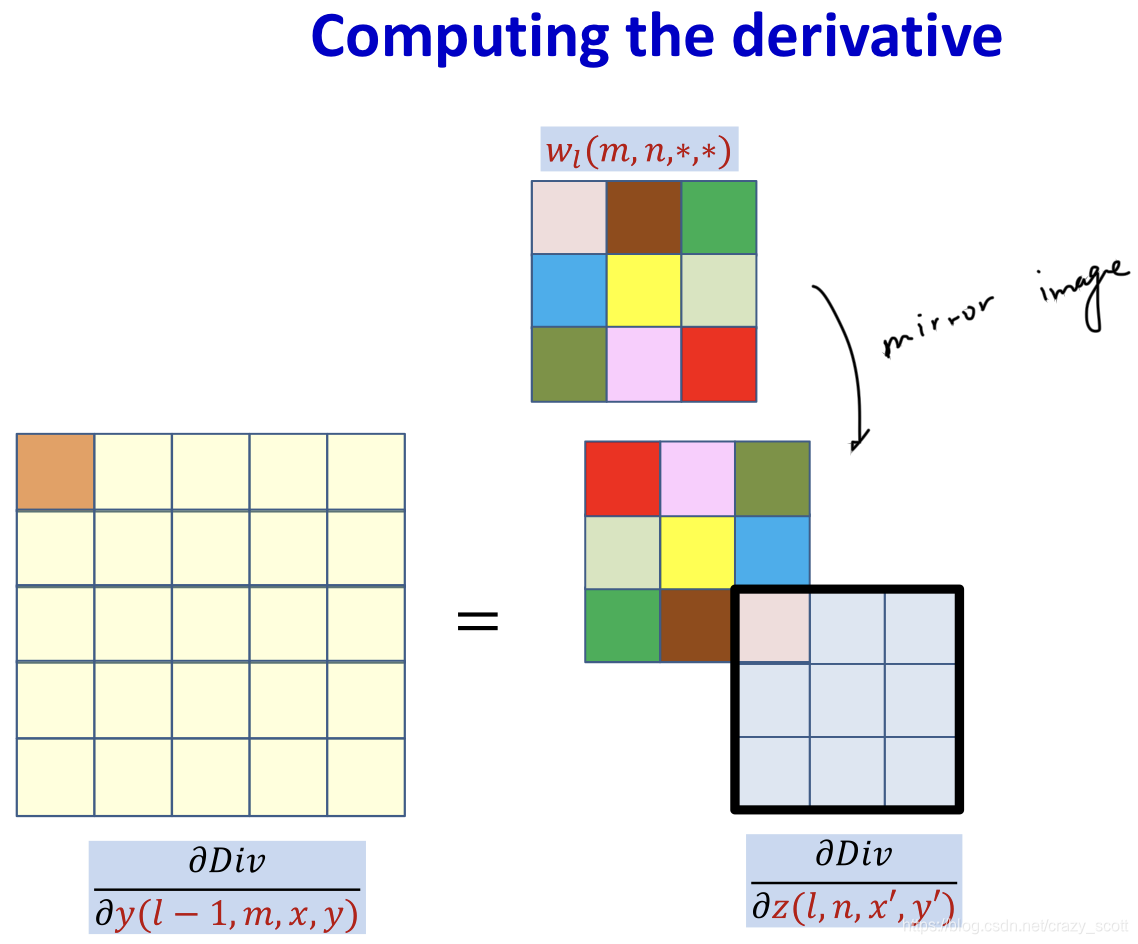
在这里插入图片描述

In practice, the derivative at each (x,y) location is obtained from all $Z$ maps

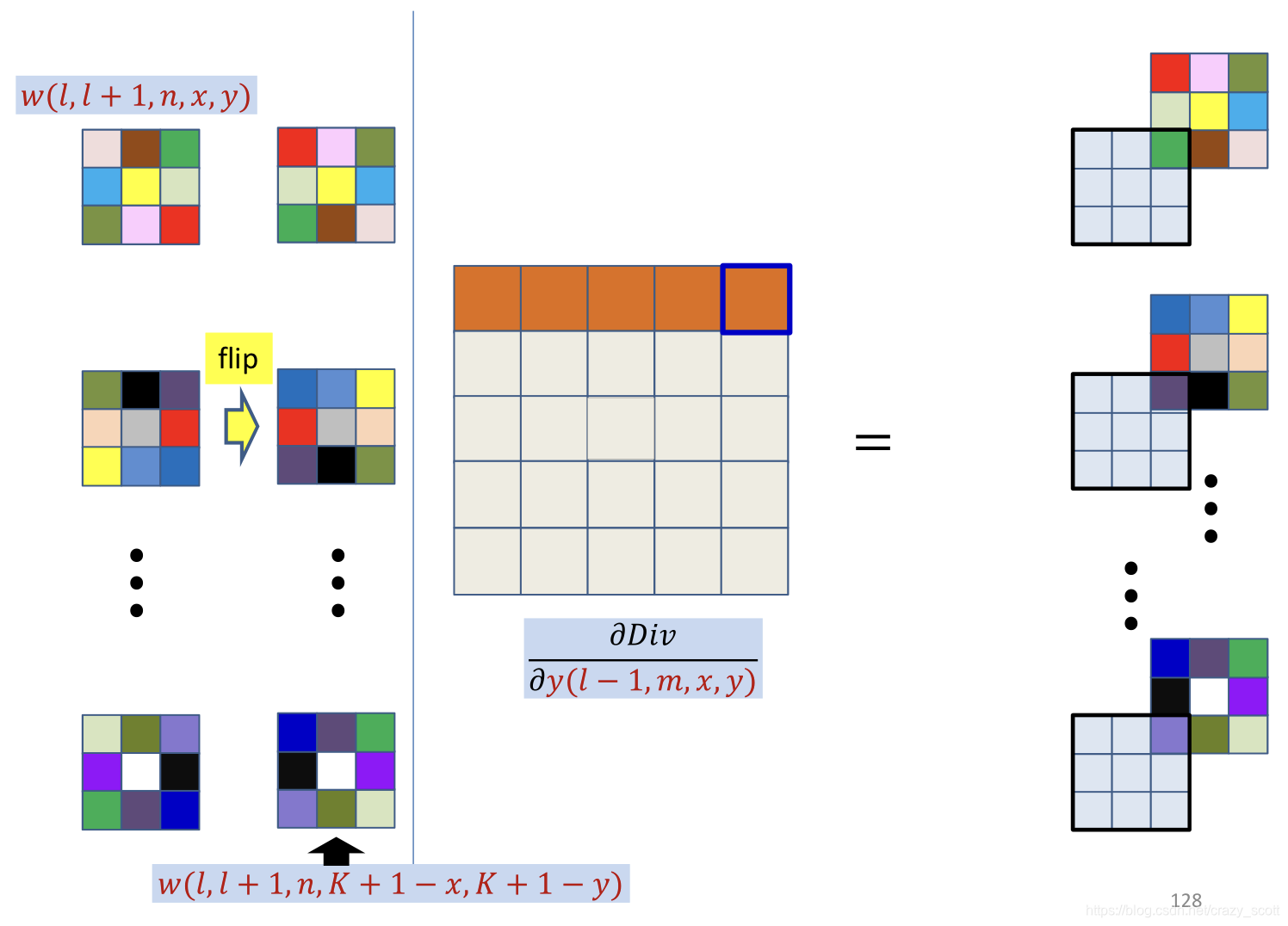
在这里插入图片描述

This is just a convolution of $\frac{\partial Div}{\partial z(l,n,x,y)}$ by the inverted filter
- After zero padding it first with $L - 1$ zeros on every side

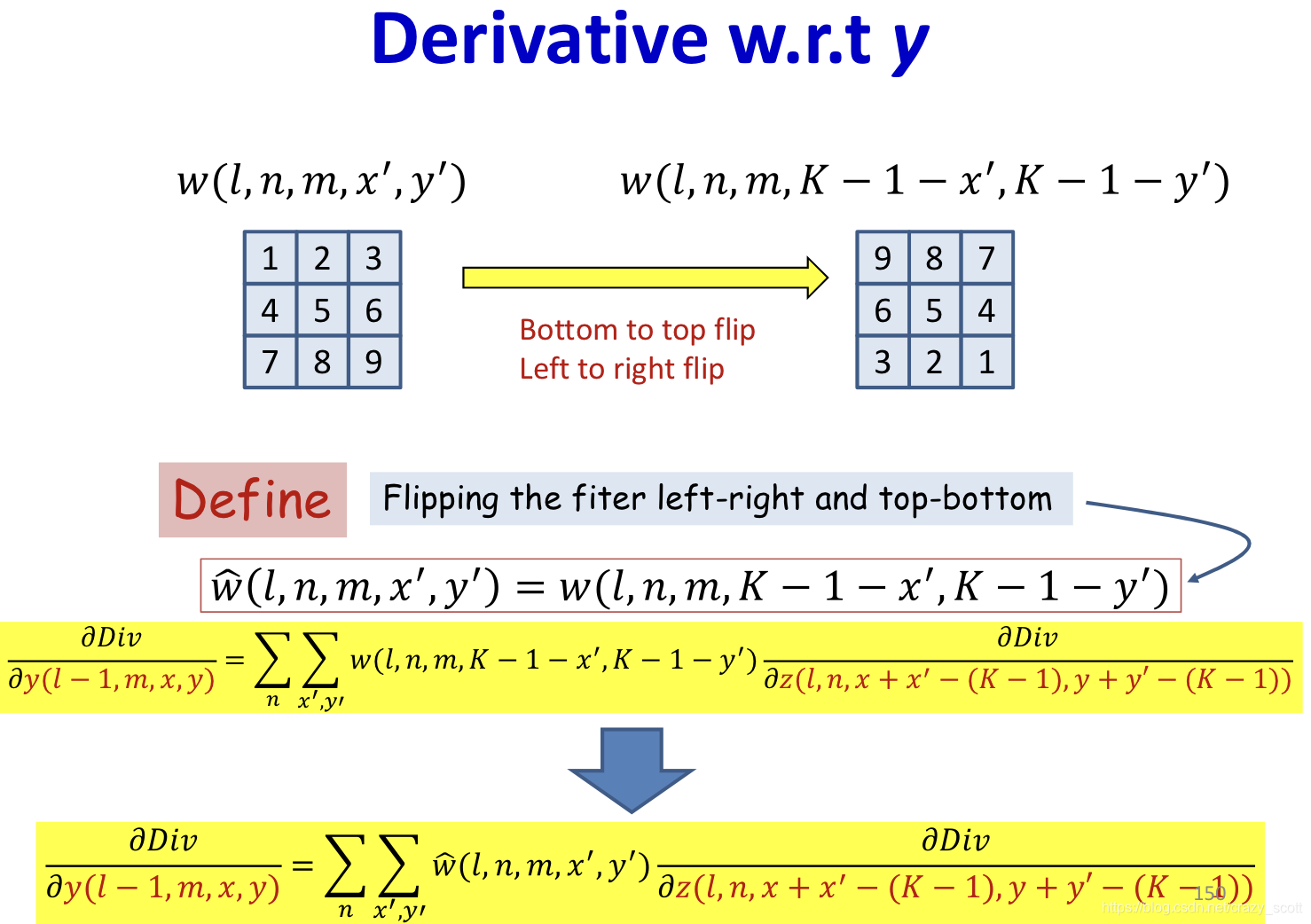
在这里插入图片描述

Note: the $x\prime, y\prime$ refer to the location in filter
Shifting down and right by $K - 1$ , such that $0, 0$ becomes $K - 1, K - 1$

$z_{\text {shift}}(l, n, m, x, y)=z(l, n, x-K+1, y-K+1)$

$\frac{\partial D i v}{\partial y(l-1, m, x, y)}=\sum_{n} \sum_{x^{\prime}, y^{\prime}} \widehat{w}\left(l, n, m, x^{\prime}, y^{\prime}\right) \frac{\partial D i v}{\partial z_{s h i f t}\left(l, n, x+x^{\prime}, y+y^{\prime}\right)}$

Regular convolution running on shifted derivative maps using flipped filter

Pooling

Pooling is typically performed with strides > 1
- Results in shrinking of the map
- Downsampling

Derivative of Max pooling

$KaTeX parse error: Got function '\newline' with no arguments as argument to '\left' at position 1: \̲n̲e̲w̲l̲i̲n̲e̲$

Max pooling selects the largest from a pool of elements ¹

在这里插入图片描述

Derivative of Mean pooling

The derivative of mean pooling is distributed over the pool

$n)=\frac{1}{K_{l p o o l}^{2}} d u(l, m, k, n)$

在这里插入图片描述

Transposed Convolution

We’ve always assumed that subsequent steps shrink the size of the maps
Can subsequent maps increase in size²

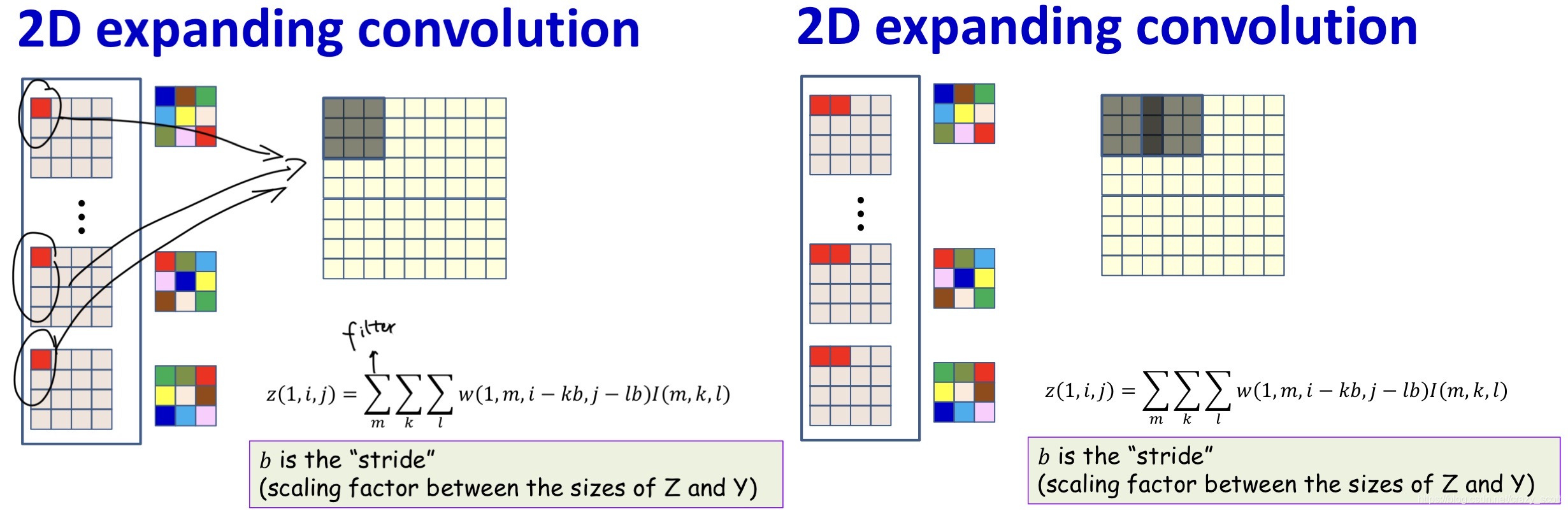
在这里插入图片描述

Output size is typically an integer multiple of input
- +1 if filter width is odd

Model variations

Very deep networks
- 100 or more layers in MLP
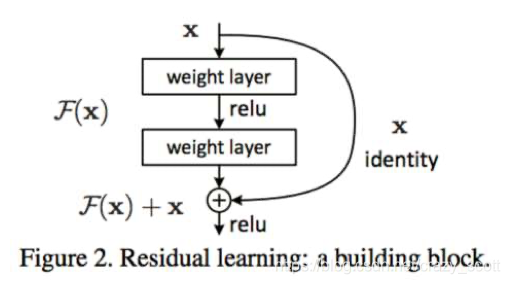
- Formalism called “Resnet”
Depth-wise convolutions
- Instead of multiple independent filters with independent parameters, use common layer-wise weights and combine the layers differently for each filter

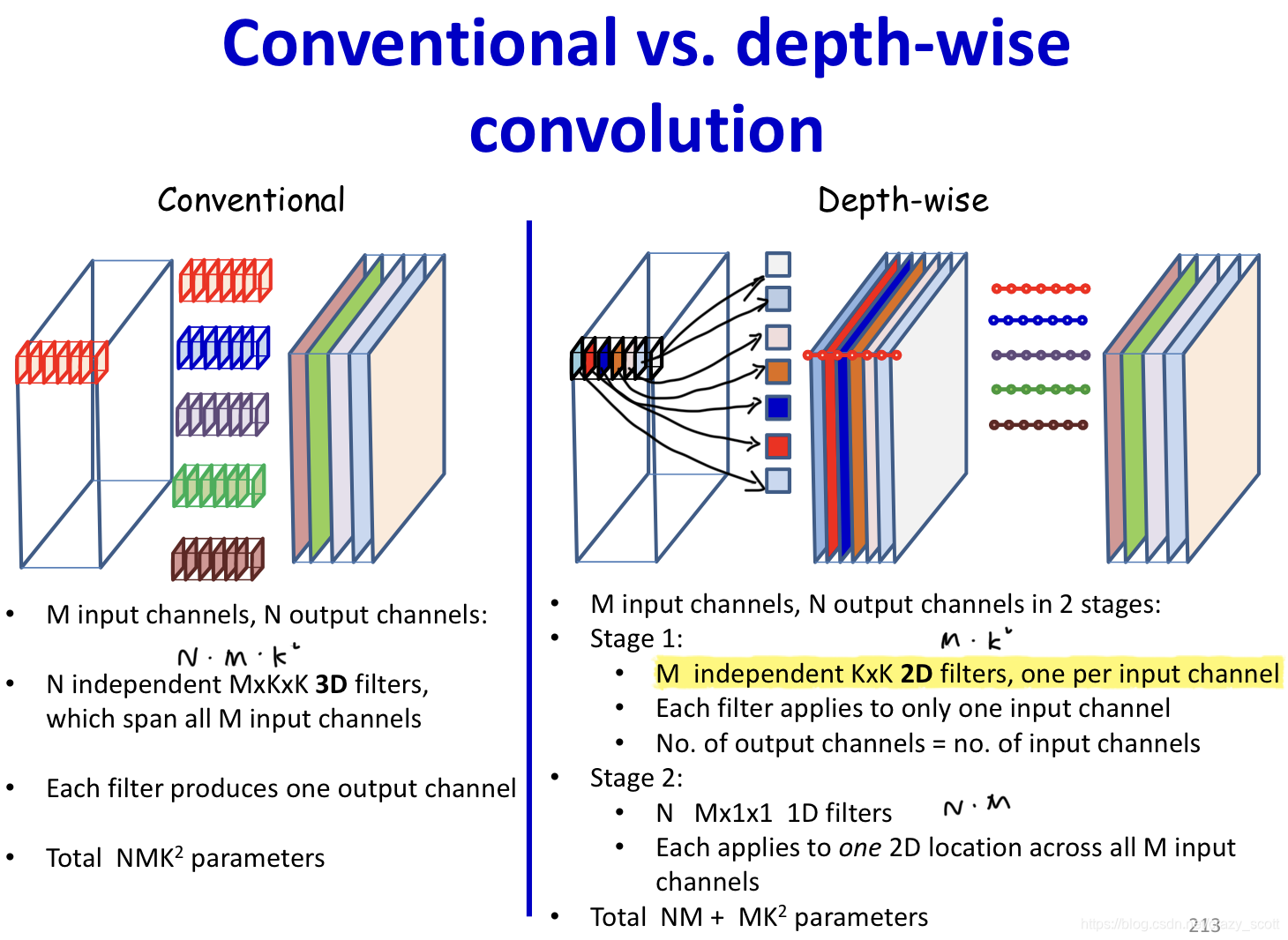
Depth-wise convolutions

In depth-wise convolution the convolution step is performed only once
The simple summation is replaced by a weighted sum across channels
- Different weights (for summation) produce different output channels

在这里插入图片描述

Models

For CIFAR 10
- Le-net 5³
For ILSVRC(Imagenet Large Scale Visual Recognition Challenge)
- AlexNet
  - NN contains 60 million parameters and 650,000 neurons
  - 5 convolutional layers, some of which are followed by max-pooling layers
  - 3 fully-connected layers
- VGGNet
  - Only used 3x3 filters, stride 1, pad 1
  - Only used 2x2 pooling filters, stride 2
  - ~140 million parameters in all
- Googlenet
  - Multiple filter sizes simultaneously
For ImageNet
- Resnet
  - Last layer before addition must have the same number of filters as the input to the module
  - Batch normalization after each convolution

在这里插入图片描述

Densenet
- All convolutional
- Each layer looks at the union of maps from all previous layers
  - Instead of just the set of maps from the immediately previous layer