acw数学知识（下）

数论基础知识

10. 高斯消元

10.1 步骤

枚举每一列c
1.找到该列绝对值最大的一行
2.换到最上面
3.将该行第一个数变成1
4.将下面所有行的第c列消成0

const int N=110;
const double eps=1e-6;
int n;
double a[N][N];

int gauss()
{
	int c,r;
	for(c=0,r=0;c<n;c++)
	{
		int t=r;
		for(int i=r;i<n;i++)
			if(fabs(a[i][c])>fabs(a[t][c]))
				t=i;
		if(fabs(a[t][c])<eps) continue;
		for(int i=c;i<=n;i++) swap(a[t][i],a[r][i]);
		for(int i=n;i>=c;i--) a[r][i]/=a[r][c];
		for(int i=r+1;i<n;i++)
			if(fabs(a[i][c])>eps)
				for(int j=n;j>=c;j--)
					a[i][j]-=a[r][j]*a[i][c];
		r++;
	}
	if(r<n) 
	{
		for(int i=r;i<n;i++)
			if(fabs(a[i][n])>eps) 
				return 2;//无解
		return 1;//无穷组解
	}
	for(int i=n-1;i>=0;i--)
		for(int j=i+1;j<n;j++)
			a[i][n]-=a[i][j]*a[j][n];
	return 0;//一组解
}

11. 组合数

11.1 递归法

$1<=b<=a<=2000$

for(int i=0;i<N;i++)
	for(int j=0;j<=i;j++)
		if(!j) c[i][j]=1;
		else c[i][j]=c[i-1][j-1]+c[i-1][j];

11.2 通过预处理逆元的方式

$1<=b<=a<=1e5$
$\because$ $\frac{a!}{b!}$ $(modp)$ $\ne$ $\frac{a!(modp)}{b!(modp)}$
所以，可以转化为：$a!\ast d!$ $(modp)$
其中，$d_i$ 为 $b_i$ 对 $p$ 的逆元，等于$b_i^{p-2}$

int fact[N],infact[N];
int qmi(int a,int k,int p)
{
	int res=1;
	while(k)
	{
		if(k&1) res=(ll)res*a%p;
		a=(ll)a*a%p;
		k>>=1;
	}
	return res;
}

fact[0]=infact[0]=1;
for(int i=1;i<N;i++)
{
	fact[i]=(ll)fact[i-1]*i%mod;
	infact[i]=(ll)infact[i-1]*qmi(i,mod-2,mod)%mod;//逆元
}

11.3 卢卡斯定理

$1<=b<=a<=1e18,1<=p<=1e5$

11.3.1定理

设$P$为素数，$a,b\in N^{\ast }$,并且
$$\begin{gathered} a=a_k\ast p^k+a_{k-1}\ast p^{k-1}+\cdot \cdot \cdot +a_1\ast p+a_0 \\ b=b_k\ast p^k+b_{k-1}\ast p^{k-1}+\cdot \cdot \cdot +b_1\ast p+b_0 \end{gathered}$$
这里$0<=a_i,b_i<=p-1$都是整数，$i=0,1,2,\cdot \cdot \cdot ,k$，则有
$$C_a^b\equiv C_{a_k}^{b_k}\ast C_{a_{k-1}}^{b_{k-1}}\ast \cdot \cdot \cdot \ast C_{a_0}^{b_0}(modP)$$

11.3.2证明

$(1+x{)}^p=C_p^0\ast 1+C_p^1\ast x+C_p^2\ast x^2+\cdot \cdot \cdot +C_p^p\ast x^p$
因为$p$是素数
所以$C_p^i\ast x_i$没有$<p$的质因子，可知$C_p^i\ast x_i\equiv 0(modp)$
得到$$(1+x{)}^p\equiv 1+x^p(modp)$$
利用上述结果，可知
$$\begin{gathered} (1+x{)}^a=(1+x{)}^{a_0}\ast ((1+x{)}^p{)}^{a_1}\ast \cdot \cdot \cdot \ast ((1+x{)}^{p_k}{)}^{a_k} \\ \equiv (1+x{)}^{a_0}\ast ((1+x^p{)}^{a_1}\ast \cdot \cdot \cdot \ast ((1+x^{p_k}{)}^{a_k}(modp) \end{gathered}$$
左右式中，$x^b$的系数相等可得
$$C_a^b\equiv C_{a_k}^{b_k}\ast C_{a_{k-1}}^{b_{k-1}}\ast \cdot \cdot \cdot \ast C_{a_0}^{b_0}(modp)$$

11.3.3代码

typedef long long ll;
int a,b,p;
int qmi(int a,int k)
{
	int res=1;
	while(k)
	{
		if(k&1) res=(ll)res*a%p;
		a=(ll)a*a%p;
		k>>=1;
	}
	return res;
}
int C(int a,int b)
{
	int res=1;
	for(int i=1,j=a;i<=b;i++,j--)
	{
		res=(ll)res*j%p;
		res=(ll)res*qmi(i,p-2)%p;
	}
	return res;
}
int lucas(ll a,ll b)
{
	if(a<p&&b<p) return C(a,b);
	return (ll)C(a%p,b%p)*lucas(a/p,b/p)%p;
}

11.4 分解质因数法求组合数

11.4.1内容

$C_a^b=\frac{a!}{b!\ast (a-b)!}$
分解质因数得
$a!=p_1^{{\alpha }_1}\ast p_2^{{\alpha }_2}\ast \cdot \cdot \cdot \ast p_k^{{\alpha }_k}$
$b!=p_1^{{\beta }_1}\ast p_2^{{\beta }_2}\ast \cdot \cdot \cdot \ast p_k^{{\beta }_k}$
$(a-b)!=p_1^{{\gamma }_1}\ast p_2^{{\gamma }_2}\ast \cdot \cdot \cdot \ast p_k^{{\gamma }_k}$
其中，
$\alpha =\lfloor \frac{a}{p}\rfloor +\lfloor \frac{a}{p^2}\rfloor +\lfloor \frac{a}{p^3}\rfloor +\cdot \cdot \cdot$
$p$的倍数的个数+$p^2$的倍数的个数+···
那么，对于$C_a^b$的某个质因数$p_i$,指数为${\alpha }_i-{\beta }_i-{\gamma }_i$

11.4.2 代码

const int N=5010;
int sum[N],primes[N],cnt;
bool st[N];
void get_primes(int n)
{
	for(int i=2;i<=n;i++)
	{
		if(!st[i]) primes[cnt++]=i;
		for(int j=0;primes[j]<=n/i;j++)
		{
			st[primes[j]*i]=true;
			if(i%primes[j]==0) break;
		}
	}
}
int get(int n,int p)//获取指数
{
	int res=0;
	while(n)
	{
		res+=n/p;
		n/=p;
	}
	return res;
}
vector<int> mul(vector<int> a,int b)//高精度乘法
{
	vector<int> c;
	int t=0;
	for(int i=0;i<(int)a.size();i++)
	{
		t+=a[i]*b;
		c.push_back(t%10);
		t/=10;
	}
	while(t)
	{
		c.push_back(t%10);
		t/=10;
	}
	return c;
}
int main()
{
	int a,b;
	cin>>a>>b;
	get_primes(a);
	for(int i=0;i<cnt;i++)
	{
		int p=primes[i];
		sum[i]=get(a,p)-get(b,p)-get(a-b,p);
	}
	vector<int> res;
	res.push_back(1);
	for(int i=0;i<cnt;i++)
		for(int j=0;j<sum[i];j++)
			res=mul(res,primes[i]);
	for(int i=res.size()-1;i>=0;i--)
		printf("%d",res[i]);
}

11.5 卡特兰数

卡特兰数是组合数学中一个常出现于各种计数问题中的数列。其前几项为（从第0项开始）：1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, …

11.5.1几何意义

给定$n$个$0$和$n$个$1$,它们将按照某种顺序排成长度为$2n$的序列，求它们能排成的所有序列中，能够满足任意前缀序列中0的个数不少于1的个数的序列有多少。
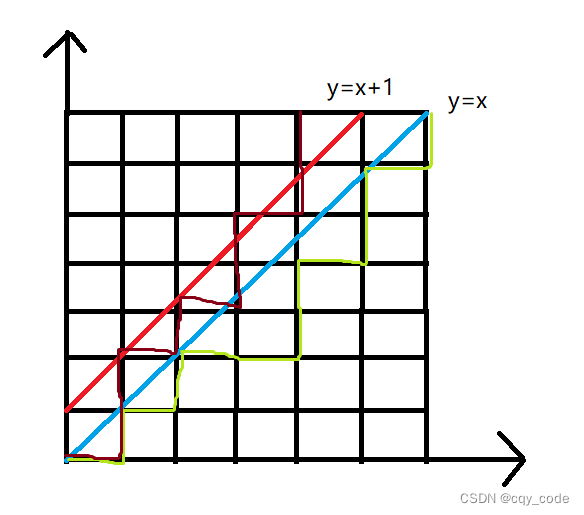
转化到二维坐标中，就是求从原点$(0,0)$出发到$(n,n)$满足已走路径始终是右移步数多于上移步数的方案数。即路线不超过直线$y=x$上部。

11.5.2推导

总方案数：从原点$(0,0)$出发到$(n,n)$，需要右移$n$步，上移$n$步才能到达终点，方案数为$C_{2n}^n$步。
触碰红线：即从原点$(0,0)$出发到$(n-1,n+1)$，方案数$C_{n-1}^{2n}$
那么合法方案数：$C_{2n}^n-C_{n-1}^{2n}$
化简后，$Catala{n}_n=\frac{1}{n+1}\ast C_{2n}^n$

12. 容斥原理

12.1基本思想

先不考虑重叠的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复，这种计数的方法称为容斥原理。
$n$个元素，奇数个加，偶数个减，一共$2^n-1$项
$|S_1\cup S_2\cup S_3|=|S_1|+|S_2|+|S_3|-|S_1\cap S_2|-|S_1\cap S_3|-|S_2\cap S_3|+|S_1\cap S_2\cap S_3|$
$C_n^1-C_n^2+C_n^3-\cdot \cdot \cdot +(-1{)}^{k-1}{C}_k^k=1$

13. 博弈论

先手必胜状态：可以走到某一个必败状态
先手必败状态：走不到任何一个必败状态

13.1Nim游戏

13.1.1 规则

有n堆石子,两个玩家轮流拿石子，每次从任意一堆中拿走任意数量的石子，不能不拿，拿到最后一个石子的玩家获胜。

13.1.2 结论

$a_1\wedge a_2\wedge \cdot \cdot \cdot \wedge a_n=0$ 先手必败
$a_1\wedge a_2\wedge \cdot \cdot \cdot \wedge a_n\ne 0$ 先手必胜