【POJ3974】Palindrome（二分+哈希）

Description

Andy the smart computer science student was attending an algorithms class when the professor asked the students a simple question, “Can you propose an efficient algorithm to find the length of the largest palindrome in a string?”

A string is said to be a palindrome if it reads the same both forwards and backwards, for example “madam” is a palindrome while “acm” is not.

The students recognized that this is a classical problem but couldn’t come up with a solution better than iterating over all substrings and checking whether they are palindrome or not, obviously this algorithm is not efficient at all, after a while Andy raised his hand and said “Okay, I’ve a better algorithm” and before he starts to explain his idea he stopped for a moment and then said “Well, I’ve an even better algorithm!”.

If you think you know Andy’s final solution then prove it! Given a string of at most 1000000 characters find and print the length of the largest palindrome inside this string.

Input

Your program will be tested on at most 30 test cases, each test case is given as a string of at most 1000000 lowercase characters on a line by itself. The input is terminated by a line that starts with the string “END” (quotes for clarity).

Output

For each test case in the input print the test case number and the length of the largest palindrome.

来源

http://poj.org/problem?id=3974

题意

输入只有小写字母构成的字符串，输出该字符串的最长回文子串长度。

思路

哈希

把任意长度的字符串映射成一个非负整数。
取固定值$P$，将字符串看成$P$进制，若两个字符串的$Hash$值相同，则认为这两个字符串相同。

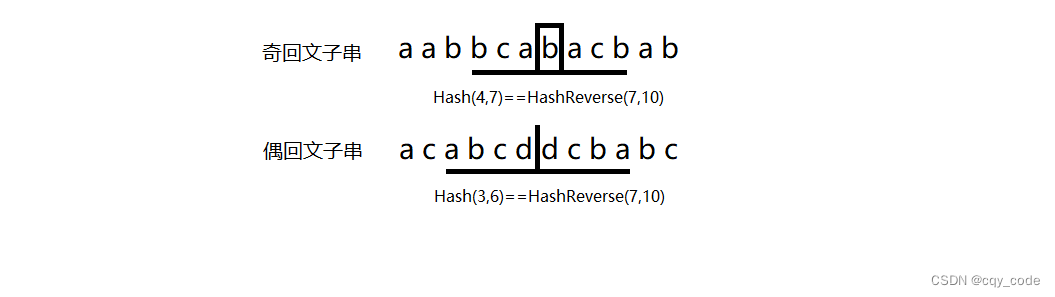
所以可以先正向预处理Hash值，再倒着做一遍预处理

$H[l-1]$
$H[l]=H[l-1]\ast p+s[l]$
$H[l+1]=H[l-1]\ast p^2+s[l]\ast p+s[l+1]$
$\dots$
$H[r]=H[l-1]\ast p^{r-l+1}+s[l]\ast p^{r-l}+...+s[r]$

那么，$$H[l...r]=s[l]\ast p^{r-l}+...+s[r]=H[r]-H[l-1]\ast c[r-l+1]$$
其中，$c[r-l+1]=p^{r-l+1}$

奇偶回文子串

在字符串头尾和每个字符中间都插入一个未出现过的字符， 长度从$n$变为$2n+1$

那么偶回文子串就会变成奇回文子串，奇回文子串还是奇回文子串。

$$aba->\#a\#b\#a\#$$

二分

遍历字符串，在每个位置$i$上寻找最长回文半径$mid$，记下最大值。

判断$Hash(i,i+mid-1)==HashReverse(i-mid+1,i)$

所以插入新字符后的回文子串最长长度为$$(i+mid-1)-i+i-(i-mid+1)-1=2\ast mid-1$$

那么原字符串的回文子串最长长度为$$mid-1$$

边界

最小半径是大于0的

最大半径是位置$i$离左右两端的最小距离

但要保证寻找的最大半径始终在二分的边界线左侧，所以右边界$r$要加一

AC代码

#include<iostream>
#include<string>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const int maxn=2e6+5;
char str[maxn>>1],s[maxn];
int t,p=31;
ll c[maxn],h1[maxn],h2[maxn];
ll calc1(int l,int r){
	return h1[r]-h1[l-1]*c[r-l+1];
}
ll calc2(int l,int r){
	return h2[l]-h2[r+1]*c[r-l+1];
}
int main(){
	while(scanf("%s",str+1)){
		if(str[1]=='E') break;
		t++;
		int len=strlen(str+1);
		int cnt=0;
		s[++cnt]='z'+1;
		for(int i=1;i<=len;i++)
			s[++cnt]=str[i],s[++cnt]='z'+1;
		c[0]=1;
		for(int i=1;i<=cnt;i++)
			c[i]=c[i-1]*p;
		for(int i=1;i<=cnt;i++)
			h1[i]=h1[i-1]*p+(s[i]-'a');
		for(int i=cnt;i;i--)
			h2[i]=h2[i+1]*p+(s[i]-'a');
		
		int ans=0;
		for(int i=1;i<=cnt;i++){
			int l=0,r=min(i,cnt-i+1)+1;
			while(l+1<r){
				int mid=(l+r)/2;
				if(calc1(i,i+mid-1)==calc2(i-mid+1,i)) l=mid;
				else r=mid;
			}
			ans=max(ans,l);
		}
		printf("Case %d: %d\n",t,ans-1);
	}
}