用泰勒公式推导梯度下降原理

什么是泰勒公式

百度百科中的解释

泰勒公式，应用于数学、物理领域，是一个用函数在某点的信息描述其附近取值的公式。如果函数足够平滑的话，在已知函数在某一点的各阶导数值的情况之下，泰勒公式可以用这些导数值做系数构建一个多项式来近似函数在这一点的邻域中的值。

说白了，泰勒公式就是：可以使用函数在某点的各阶导数组成高次多项式去逼近一个函数。
泰勒公式表示为：
$$\mathrm{h}(\mathrm{x})=\sum _{k=0}^{\infty }\frac{{\mathrm{h}}^{(k)}\left(x_0\right)}{k!}{\left(x-x_0\right)}^k$$将泰勒公式展开：
$$\begin{array}{rl}\mathrm{h}(\mathrm{x})& =\sum _{k=0}^{\infty }\frac{{\mathrm{h}}^{(k)}\left(x_0\right)}{k!}{\left(x-x_0\right)}^k\\ & =h\left(x_0\right)+h^{\prime }\left(x_0\right)\left(x-x_0\right)+\frac{h^{\prime \prime }\left(x_0\right)}{2!}{\left(x-x_0\right)}^2+\dots \end{array}$$同时，如果$x$ 很接近 $x_0$，也就是逼近的范围足够小的话，上面的公式可以只取前两项：
$$h(x)\approx h\left(x_0\right)+h^{\prime }\left(x_0\right)\left(x-x_0\right)$$上面的公式是变量为一维的时候得出的，对于多维变量，只不过将求导改为分别求偏导即可。

---

泰勒公式和梯度下降的关系

想象一下在多维空间中有下面的图像（它的函数$L(\mathbf{\theta })$自变量为${\theta }_1$ 和 ${\theta }_2$），从红色到紫色表示海拔越来越低，那么任取空间中一个点${\theta }_0$ 后，每次移动一步，如何才能更快的到达谷底。

为了方便用公式推导出最速下降的关系，可以设定每次在极小的范围内移动一步，因此就可以将$L(\mathbf{\theta })$ 用泰勒展开来逼近。将走这一小步到达的点记为$\left(a,b\right)$，则有泰勒展开如下：

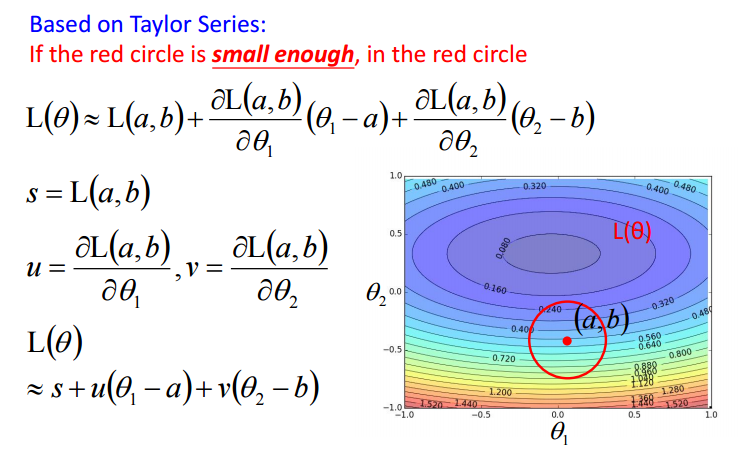
上面的式子即被简化成了：
$$\begin{array}{l}\mathrm{L}(\theta )\approx s+u\left({\theta }_1-a\right)+v\left({\theta }_2-b\right)\end{array}$$因为$s$ 是一个定值，只与输入有关，因此不去看它，只考虑$u\left({\theta }_1-a\right)+v\left({\theta }_2-b\right)$.

将$u$ 与 $v$ 合在一起作为一个向量${\nabla }_{w}f(x)$（这其实就是对所有变量分别求偏导的集合），将$\left({\theta }_1-a\right)$与$\left({\theta }_2-b\right)$作为另外一个向量$\mathbf{u}$（距离尽可能小，可以视为单位向量），想让$L(\mathbf{\theta })$最小，也即让两个向量的点积最小，也就是：
$$\begin{gathered} \min {\mathbf{u}}^{\top }{\nabla }_{\mathbf{x}}f(\mathbf{x}) \\ =\min \Vert \mathbf{u}{\Vert }_2{\Vert {\nabla }_{\mathbf{x}}f(\mathbf{x})\Vert }_2\cos \theta \end{gathered}$$想让上面的式子取最小值，很显然要令两个向量方向相反，也就是：下降的方向与梯度方向相反。