佩尔方程
若一个丢番图方程具有以下的形式:
且 为正整数,则称此二元二次不定方程为佩尔方程(英文:Pell's equation 德文:Pellsche Gleichung)
为正整数,则称此二元二次不定方程为佩尔方程(英文:Pell's equation 德文:Pellsche Gleichung)
若 是完全平方数,则这个方程式只有解
是完全平方数,则这个方程式只有解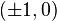 (实际上对任意的
(实际上对任意的 ,
,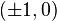 都是解)。对于其余情况,拉格朗日证明了佩尔方程总有解。而这些解可由
都是解)。对于其余情况,拉格朗日证明了佩尔方程总有解。而这些解可由 的连分数求出。
的连分数求出。
佩尔方程的解
设 是
是 的连分数表示:
的连分数表示:![[a_{0}; a_{1}, a_{2}, a_{3}, \,\ldots ]](http://upload.wikimedia.org/math/d/5/5/d5591a1cd2d18fba954047213cb43e1f.png) 的渐近分数列,由连分数理论知存在
的渐近分数列,由连分数理论知存在
 使得(pi,qi) 为佩尔方程的解。取其中最小的
使得(pi,qi) 为佩尔方程的解。取其中最小的
 ,将对应的 (pi,qi) 称为佩尔方程的基本解,或最小解,记作(x1,y1)
,则所有的解(xi,yi) 可表示成如下形式:
,将对应的 (pi,qi) 称为佩尔方程的基本解,或最小解,记作(x1,y1)
,则所有的解(xi,yi) 可表示成如下形式:
或者由以下递推公式得到:





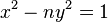

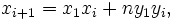
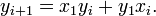

















 462
462

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








