自动化专业用Python干什么？——单入单出二阶系统PID控制

在上篇文章的基础上，加入PID控制（实际只使用了PD控制）

上篇文章请看：https://blog.youkuaiyun.com/congguitar/article/details/106801306

 

还是这个二阶系统，选取系统参数：a1=2，a2=2

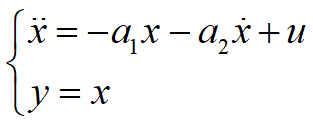
1理论计算

设r为期望值，则我们设计PD控制器为：

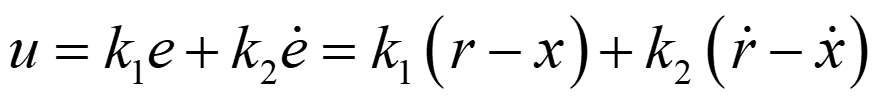
将控制器代入到系统方程中得到闭环系统为

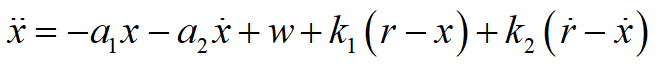
我们来考察系统的节约响应，即令r=1，则其导数为0

进一步得到系统闭环方程：

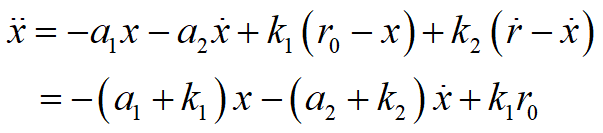
对应的传递函数为：

 

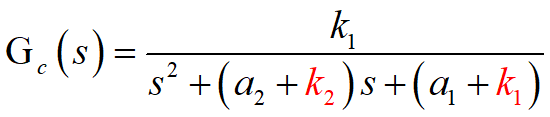
我们通过极点配置的方法确定k1和k2

假设我系统的极点为

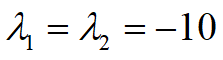
则通过计算得到：k1=98和k2=18，得到控制器参数。

2 程序部分

import math
import numpy as np
import matplotlib.pyplot as plt

def runge_kutta(y,h,f):
    k1 = h*f(t,x1,x2)
    k2 = h*f(t+0.5*k1,x1+0.5*k1,x2+0.5*k1)
    k3 = h*f(t+0.5*k2,x1+0.5*k2,x2+0.5*k2)
    k4 = h*f(t+k3,x1+k3,x2+k3)
    return y+(k1+2*k2+2*k3+k4)/6.
def func_x1(t,x1,x2):
    return x2
def func_x2(t,x1,x2):
    return -2*x1-2*x2+u
def control(e,de):
    return kp*e+kd*de
if __name__=='__main__':
#initial
#Ts
    dt = .001
#state
    t = 0;u = 0;r = 1;
    x1 = 0;x2 = 0;
    e = r-x1;e_ = e;
    rs,x1s,x2s,ds,us,ts=[],[],[],[],[],[]
#control
    kp=100
    kd=20
#Run
    while t <= 10:
        #r =math.cos(t)
        x1=runge_kutta(x1,dt,func_x1)
        x2=runge_kutta(x2,dt,func_x2)
        e =r-x1;
        de=(e-e_)/dt
        e_=e
        u =control(e,de) 
        t+= dt
        rs.append(r)
        x1s.append(x1)
        x2s.append(x2)
        us.append(u)
        ts.append(t)
#Plot       
    plt.plot(ts, rs, label='ref')
    plt.plot(ts, x1s, label='y', linestyle='--')
    plt.legend();plt.grid();plt.show()
    plt.plot(ts, x2s, label='x2')
    plt.legend();plt.grid();plt.show()
    plt.plot(ts, us, label='u')
    plt.legend();plt.grid();plt.show()

3结果部分

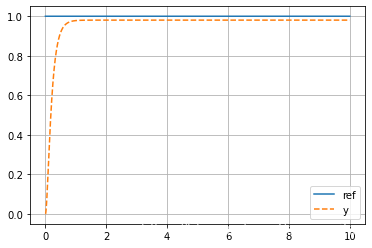
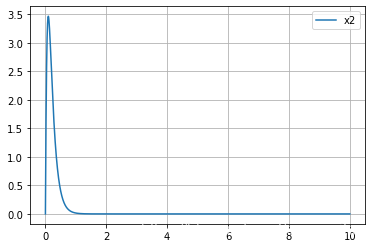
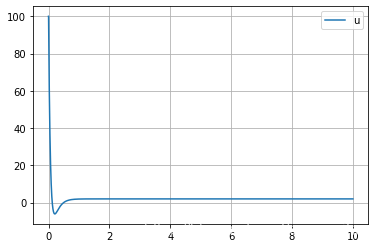
4说明

1）我是在手机上用termux，然后jupyter来编写的。还是挺好玩的

2）然后就成功了!

(版权所有，转载请注明)