文章目录
- 一元函数微分学
- 一元函数微分学相关命题的常见反例
- 函数 y = cos ∣ x ∣ y = \cos|x| y=cos∣x∣ 是否可导
- 间断点
- ∣ x ∣ a + ∣ y ∣ b = 1 \sqrt{\frac{\left|x\right|}{a}}+\sqrt{\frac{\left|y\right|}{b}}=1 a∣x∣+b∣y∣=1的图像长什么样?(星形线的图像)
- 曲率计算公式
- 比较 ( sin x ) a (\sin x)^a (sinx)a 和 sin ( x a ) \sin(x^a) sin(xa),以及 ( tan x ) a (\tan x)^a (tanx)a 和 tan ( x a ) \tan(x^a) tan(xa)
- 变上限积分函数
- 零点个数问题(求方程根的个数问题)
- 函数的凹凸性
- 极值点与拐点
一元函数微分学
一元函数微分学相关命题的常见反例
- 狄利克雷函数: f ( x ) f(x) f(x)不连续
- sin 1 x \sin\frac{1}{x} sinx1(震荡间断点)
下面这题选B,请你为其他三个选项分别举出反例
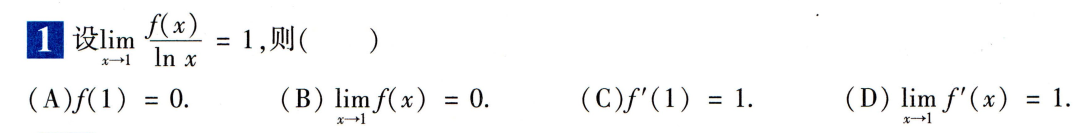

函数 y = cos ∣ x ∣ y = \cos|x| y=cos∣x∣ 是否可导
1. 当
x
>
0
x > 0
x>0 时
∣
x
∣
=
x
|x| = x
∣x∣=x,函数为
y
=
cos
x
y = \cos x
y=cosx,其导数为
y
′
=
−
sin
x
y' = -\sin x
y′=−sinx,显然可导。
2. 当
x
<
0
x < 0
x<0 时
∣
x
∣
=
−
x
|x| = -x
∣x∣=−x,函数为
y
=
cos
(
−
x
)
=
cos
x
y = \cos(-x) = \cos x
y=cos(−x)=cosx(余弦函数是偶函数),其导数为
y
′
=
−
sin
x
y' = -\sin x
y′=−sinx,同样可导。
3. 当
x
=
0
x = 0
x=0 时
需通过左右导数判断:
- 右导数( x → 0 + x \to 0^+ x→0+): lim Δ x → 0 + cos Δ x − cos 0 Δ x = lim Δ x → 0 + cos Δ x − 1 Δ x = 0 \lim_{\Delta x \to 0^+} \frac{\cos\Delta x - \cos0}{\Delta x} = \lim_{\Delta x \to 0^+} \frac{\cos\Delta x - 1}{\Delta x} = 0 limΔx→0+ΔxcosΔx−cos0=limΔx→0+ΔxcosΔx−1=0(等价无穷小替换: cos Δ x − 1 ∼ − 1 2 Δ x 2 \cos\Delta x - 1 \sim -\frac{1}{2}\Delta x^2 cosΔx−1∼−21Δx2)。
- 左导数( x → 0 − x \to 0^- x→0−): lim Δ x → 0 − cos ( − Δ x ) − cos 0 Δ x = lim Δ x → 0 − cos Δ x − 1 Δ x = 0 \lim_{\Delta x \to 0^-} \frac{\cos(-\Delta x) - \cos0}{\Delta x} = \lim_{\Delta x \to 0^-} \frac{\cos\Delta x - 1}{\Delta x} = 0 limΔx→0−Δxcos(−Δx)−cos0=limΔx→0−ΔxcosΔx−1=0。
左右导数相等(均为0),因此 x = 0 x = 0 x=0 处也可导。
结论:函数 y = cos ∣ x ∣ y = \cos|x| y=cos∣x∣ 在 全体实数域 R \mathbb{R} R 上处处可导,其导数为 y ′ = − sin x y' = -\sin x y′=−sinx。
间断点
看下面这个题,这个题要是会了,基本上间断点的题就再也难不倒你了


∣ x ∣ a + ∣ y ∣ b = 1 \sqrt{\frac{\left|x\right|}{a}}+\sqrt{\frac{\left|y\right|}{b}}=1 a∣x∣+b∣y∣=1的图像长什么样?(星形线的图像)
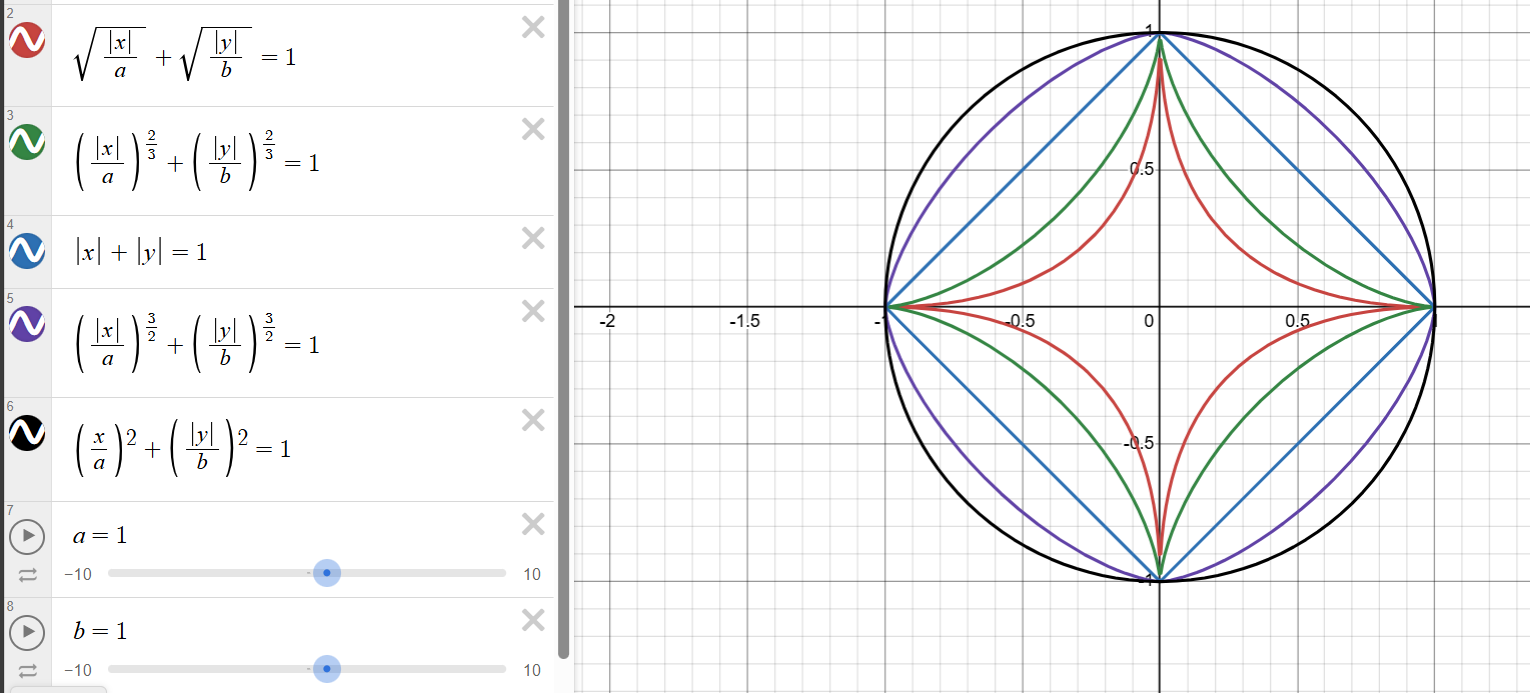
曲率计算公式
直角坐标下的曲率计算公式
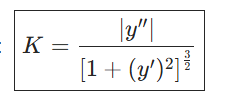
参数方程的曲率计算公式
推导过程如下

极坐标下的曲率计算公式
这个我们就是用上面的参数方程公式来做的

曲线在某点的曲率圆圆心位于该点切线的“法线方向”,但到底在切线的哪一侧?上方还是下方?
这是曲率中一个非常关键但容易混淆的问题。
答案非常明确: 曲率圆圆心在曲线的凹侧(concave side)
也就是说曲线向哪边“弯”,圆心就在哪边,即圆心的位置和曲线的凹凸性有关。
如果该曲线在该点二阶可导,那么我们就可以通过该点二阶导的正负来判断圆心的位置,即计算 f ′ ′ ( x 0 ) f''(x_0) f′′(x0)
- 若 f ′ ′ > 0 f''>0 f′′>0:圆心在上侧
- 若 f ′ ′ < 0 f''<0 f′′<0:圆心在下侧
(更一般的非函数形式也可以通过 r ⃗ ′ ′ \vec r'' r′′ 与 T ⃗ \vec T T 的方向关系判断。)
📌 用一句话总结
曲率圆圆心永远在曲线的凹侧。
凹向上 → 圆心在上;凹向下 → 圆心在下。
比较 ( sin x ) a (\sin x)^a (sinx)a 和 sin ( x a ) \sin(x^a) sin(xa),以及 ( tan x ) a (\tan x)^a (tanx)a 和 tan ( x a ) \tan(x^a) tan(xa)
完整题目:在 x→0⁺,0<x<1,a>1 的情况下,比较
(
sin
x
)
a
(\sin x)^a
(sinx)a 和
sin
(
x
a
)
\sin(x^a)
sin(xa),以及
(
tan
x
)
a
(\tan x)^a
(tanx)a 和
tan
(
x
a
)
\tan(x^a)
tan(xa)。
解题思路1:通过泰勒展开来估计
1️⃣ ( sin x ) a (\sin x)^a (sinx)a 和 sin ( x a ) \sin(x^a) sin(xa)
在 x → 0 x\to0 x→0 时:
sin x = x − x 3 6 + O ( x 5 ) \sin x = x-\frac{x^3}{6}+O(x^5) sinx=x−6x3+O(x5)
sin ( x a ) = x a − x 3 a 6 + O ( x 5 a ) \sin(x^a)=x^a-\frac{x^{3a}}{6}+O(x^{5a}) sin(xa)=xa−6x3a+O(x5a)
( sin x ) a = ( x − x 3 6 + O ( x 5 ) ) a = x a ( 1 − x 2 6 + O ( x 4 ) ) a ≈ x a ( 1 − a 6 x 2 ) (\sin x)^a =\big(x-\frac{x^3}{6}+O(x^5)\big)^a = x^a\Big(1-\frac{x^2}{6}+O(x^4)\Big)^a \approx x^a\Big(1-\frac{a}{6}x^2\Big) (sinx)a=(x−6x3+O(x5))a=xa(1−6x2+O(x4))a≈xa(1−6ax2)
于是
( sin x ) a − sin ( x a ) ≈ x a ( 1 − a 6 x 2 ) − ( x a − x 3 a 6 ) = 1 6 ( x 3 a − a x a + 2 ) = 1 6 x a + 2 ( x 2 a − 2 − a ) (\sin x)^a-\sin(x^a) \approx x^a\Big(1-\frac{a}{6}x^2\Big)-\Big(x^a-\frac{x^{3a}}{6}\Big) = \frac{1}{6}\big(x^{3a}-a x^{a+2}\big) = \frac{1}{6}x^{a+2}\big(x^{2a-2}-a\big) (sinx)a−sin(xa)≈xa(1−6ax2)−(xa−6x3a)=61(x3a−axa+2)=61xa+2(x2a−2−a)
对
0
<
x
<
1
,
a
>
1
0<x<1,a>1
0<x<1,a>1 有
x
2
a
−
2
<
1
<
a
x^{2a-2}<1<a
x2a−2<1<a,所以
x
2
a
−
2
−
a
<
0
x^{2a-2}-a<0
x2a−2−a<0,从而
( sin x ) a − sin ( x a ) < 0 (\sin x)^a-\sin(x^a)<0 (sinx)a−sin(xa)<0
即
( sin x ) a < sin ( x a ) ( x → 0 + , a > 1 ) \boxed{(\sin x)^a < \sin(x^a)\quad(x\to0^+,a>1)} (sinx)a<sin(xa)(x→0+,a>1)
2️⃣ ( tan x ) a (\tan x)^a (tanx)a 和 tan ( x a ) \tan(x^a) tan(xa)
同样在 x → 0 x\to0 x→0 时:
tan x = x + x 3 3 + O ( x 5 ) \tan x = x+\frac{x^3}{3}+O(x^5) tanx=x+3x3+O(x5)
tan ( x a ) = x a + x 3 a 3 + O ( x 5 a ) \tan(x^a)=x^a+\frac{x^{3a}}{3}+O(x^{5a}) tan(xa)=xa+3x3a+O(x5a)
( tan x ) a = ( x + x 3 3 + O ( x 5 ) ) a = x a ( 1 + x 2 3 + O ( x 4 ) ) a ≈ x a ( 1 + a 3 x 2 ) (\tan x)^a=\big(x+\frac{x^3}{3}+O(x^5)\big)^a = x^a\Big(1+\frac{x^2}{3}+O(x^4)\Big)^a \approx x^a\Big(1+\frac{a}{3}x^2\Big) (tanx)a=(x+3x3+O(x5))a=xa(1+3x2+O(x4))a≈xa(1+3ax2)
于是
( tan x ) a − tan ( x a ) ≈ x a ( 1 + a 3 x 2 ) − ( x a + x 3 a 3 ) = 1 3 ( a x a + 2 − x 3 a ) = 1 3 x a + 2 ( a − x 2 a − 2 ) (\tan x)^a-\tan(x^a) \approx x^a\Big(1+\frac{a}{3}x^2\Big)-\Big(x^a+\frac{x^{3a}}{3}\Big) = \frac{1}{3}\big(a x^{a+2}-x^{3a}\big) = \frac{1}{3}x^{a+2}\big(a-x^{2a-2}\big) (tanx)a−tan(xa)≈xa(1+3ax2)−(xa+3x3a)=31(axa+2−x3a)=31xa+2(a−x2a−2)
对
0
<
x
<
1
,
a
>
1
0<x<1,a>1
0<x<1,a>1 有
x
2
a
−
2
<
1
<
a
x^{2a-2}<1<a
x2a−2<1<a,所以
a
−
x
2
a
−
2
>
0
a-x^{2a-2}>0
a−x2a−2>0,从而
( tan x ) a − tan ( x a ) > 0 (\tan x)^a-\tan(x^a)>0 (tanx)a−tan(xa)>0
即
( tan x ) a > tan ( x a ) ( x → 0 + , a > 1 ) \boxed{(\tan x)^a > \tan(x^a)\quad(x\to0^+,a>1)} (tanx)a>tan(xa)(x→0+,a>1)
结论(在 x x x 近 0、 0 < x < 1 0<x<1 0<x<1、 a > 1 a>1 a>1 时):
( sin x ) a < sin ( x a ) , ( tan x ) a > tan ( x a ) . (\sin x)^a < \sin(x^a),\qquad (\tan x)^a > \tan(x^a). (sinx)a<sin(xa),(tanx)a>tan(xa).
解题思路2:通过构造差值函数,讨论差值函数的值域来判断

变上限积分函数
变上限积分函数是否一定可导?是否一定连续?

变上限积分函数的可导性由被积函数的连续性决定:
- 若被积函数连续,则变上限积分函数可导;
- 若被积函数不连续(仅可积),则变上限积分函数仅连续,在被积函数的间断点处不可导。
如果F(x)是f(x)的原函数,请问F(x)要满足哪些要求?
- F(x)与f(x)有着相同的定义域。
- F(x)在定义域内连续
- 如果f(x)在某点处连续,则F(x)在该点肯定可导,并且导数就是f(x)
如果导函数f(x)在定义域内无界,请问他的原函数F(x)是否可能存在?

如果一个函数f(x)存在原函数F(x),但是f(x)在定义域内不是处处连续的,请问f(x)的间断点类型是?
只可能是震荡间断点! 不可能是第一类间断点和无穷间断点。理由说明如下
首先如果 F ( x ) F(x) F(x)是 f ( x ) f(x) f(x)的原函数,那他就要满足定义,即对于定义域内任意一点 x 0 x_0 x0,都有 F ′ ( x ) = f ( x ) F'(x) = f(x) F′(x)=f(x),间断点也不例外
假设
x
0
x_0
x0是
f
(
x
)
f(x)
f(x)的可去间断点,则
lim
x
→
x
0
+
f
(
x
)
=
lim
x
→
x
0
−
f
(
x
)
=
A
≠
f
(
x
0
)
\lim_{x \to x_0^+} f(x) = \lim_{x \to x_0^-} f(x) = A \neq f(x_0)
x→x0+limf(x)=x→x0−limf(x)=A=f(x0)
而按照导数的定义
F
′
(
x
0
)
=
A
≠
f
(
x
0
)
F'(x_0) = A \neq f(x_0)
F′(x0)=A=f(x0)
这就不符合原函数的定义,出现了矛盾
假设
x
0
x_0
x0是
f
(
x
)
f(x)
f(x)的可去间断点,则
lim
x
→
x
0
+
f
(
x
)
=
A
,
lim
x
→
x
0
−
f
(
x
)
=
B
\lim_{x \to x_0^+} f(x) =A, \lim_{x \to x_0^-} f(x) = B
x→x0+limf(x)=A,x→x0−limf(x)=B
根据导数的定义,
F
(
x
)
F(x)
F(x)在
x
0
x_0
x0处的导数不存在,而原函数的定义要求F(x)在定义域内处处可导,并且导数始终等于f(x),因此也出现了矛盾
假设 x 0 x_0 x0是 f ( x ) f(x) f(x)的可去间断点,依然很容易证明, F ( x ) F(x) F(x)在 x 0 x_0 x0处的导数不存在,道理同上
零点个数问题(求方程根的个数问题)
这类问题从本质上说就是研究函数在给定区间内的形态问题,看下面这个例子
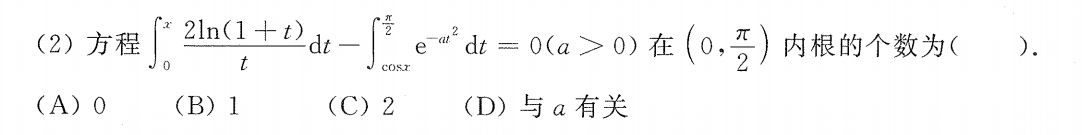
初学者看到这种问题就蒙了,我以前只学过一元二次方程的根的求解,你这方程长这么丑,怎么解啊?其实这题没想让你解方程
F ( x ) = ∫ 0 x 2 ln ( 1 + t ) t d t − ∫ cos x π 2 e − a t 2 d t F(x)=\int_{0}^{x} \frac{2\ln(1+t)}{t}dt - \int_{\cos x}^{\frac{\pi}{2}} \mathrm{e}^{-at^2} dt F(x)=∫0xt2ln(1+t)dt−∫cosx2πe−at2dt
题目其实就是想让你研究一下 F ( x ) F(x) F(x)在 ( 0 , π 2 ) \left(0,\frac{\pi}{2}\right) (0,2π)内有几个零点,那应该怎么研究呢?
- 首先我们要确定区间端点处函数值的正负
- 然后我们再判断 F ( x ) F(x) F(x)在给定区间内的单调性(如何判断单调性呢,其实就是求导,判断导函数的正负)
对本题而言,显然 F ( 0 ) > 0 , F ( π 2 ) < 0 F(0)>0,F(\frac{\pi}{2})<0 F(0)>0,F(2π)<0,那其实任务就落在判断单调性上了,对 F ( x ) F(x) F(x)求导
F ′ ( x ) = 2 ln ( 1 + x ) x − e − a cos 2 x sin x F'(x) = \frac{2\ln(1+x)}{x} - e^{-a\cos^2 x} \sin x F′(x)=x2ln(1+x)−e−acos2xsinx
导完之后我们发现吓哭了,这tm减号两边在定义域内都是正的,正负咋判断啊?这玩意又长这么丑,我死活都不能再导了啊
这就是这个题最难的点,解决方案也很直接,就是分别求减号两边的两个式子的值域,具体的解题过程如下
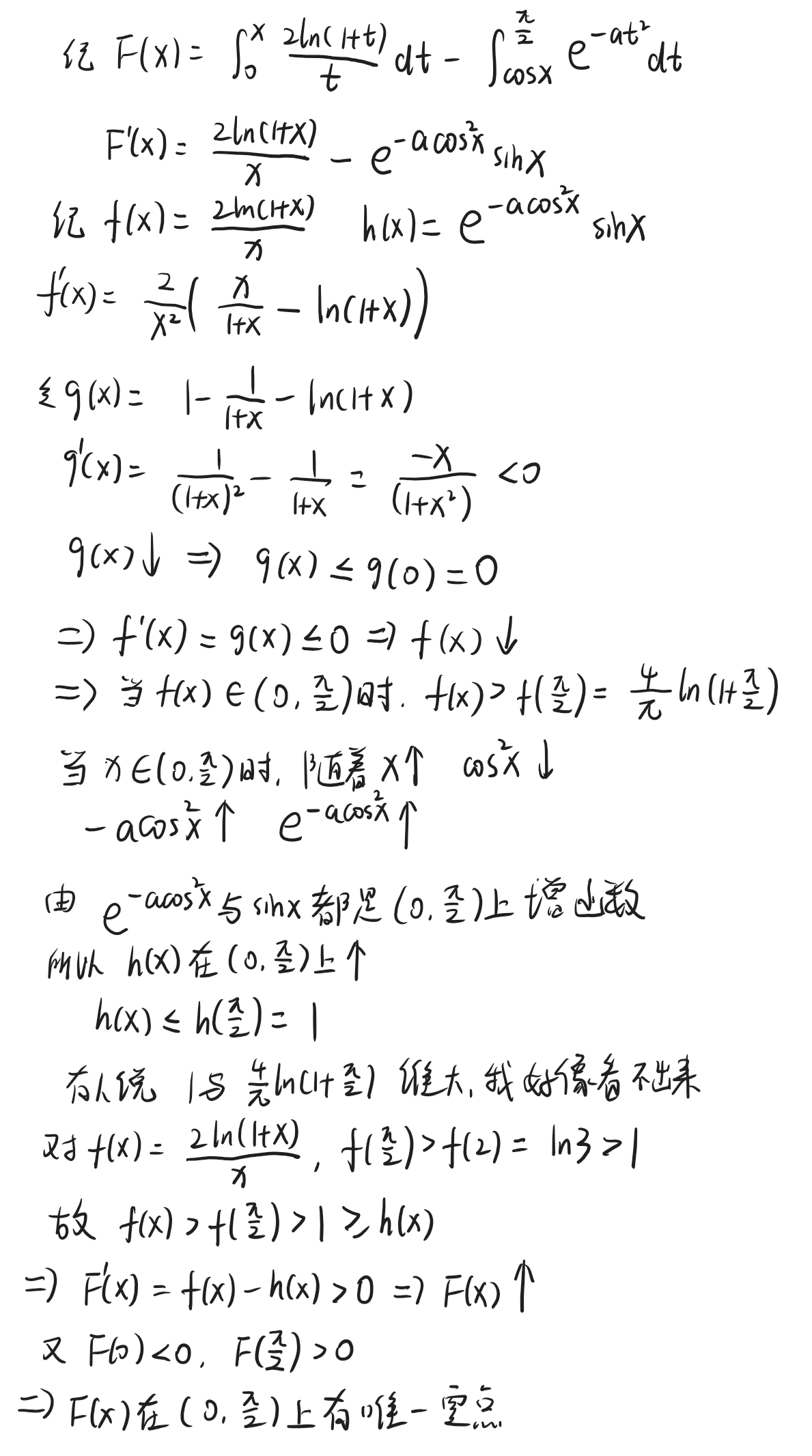
函数的凹凸性
谈论凹凸性是不是必须要求函数可导?
不是,下面是华师数分书上关于凹凸性的定义

在下图中,f(x)并不是处处可导的,但是我们在函数中任意取两点,拉根线,发现函数始终在这根线下方或在这根线上,这就说明函数是一个凸函数
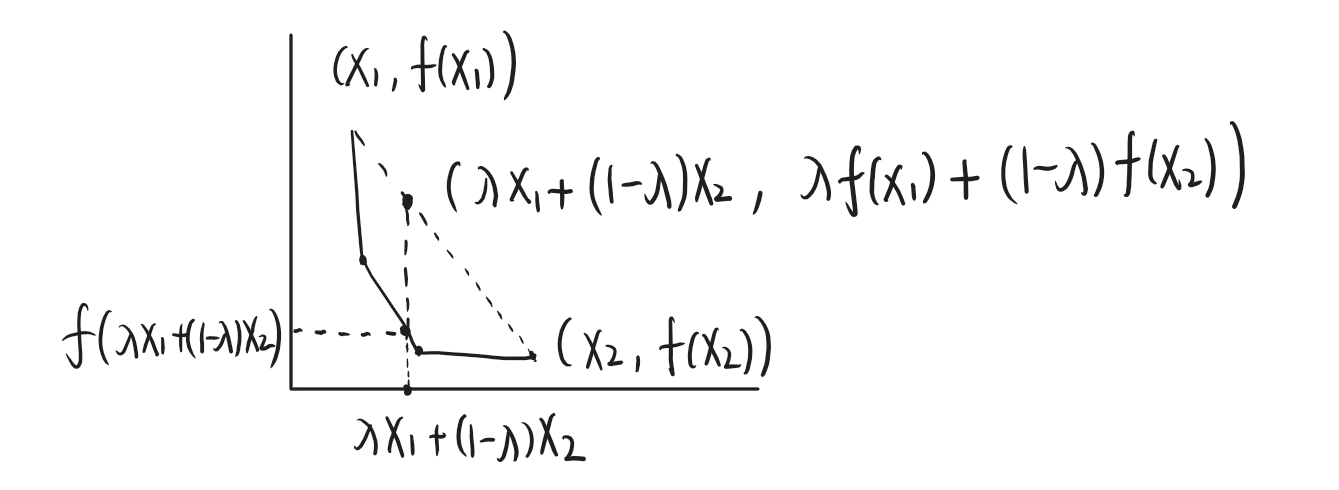
虽然凹凸性不能保证f(x)在对应区间内可导,但是它却能保证f(x)在区间内任意一点的左右导数都存在(只是不一定相等)

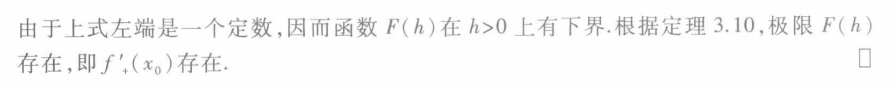
凹凸性的充要条件

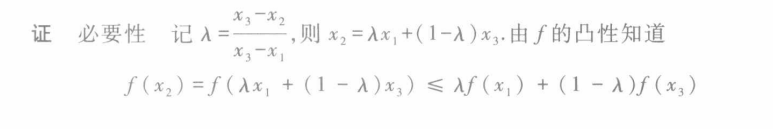
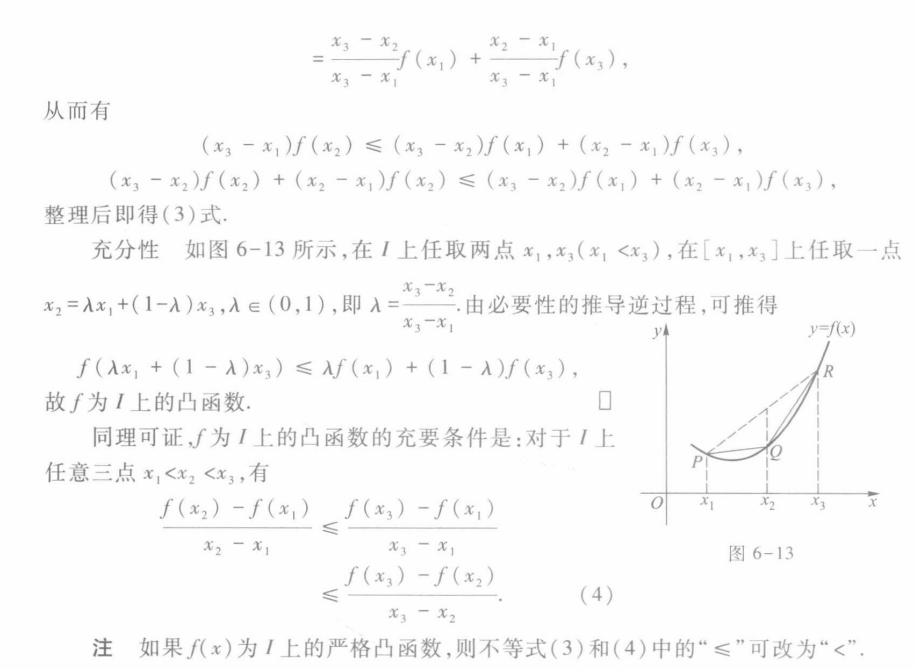
凹凸性的等价论断



定义域内二阶可导的函数是凸函数的充要条件

Jensen不等式
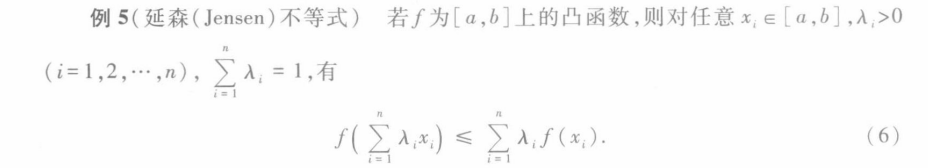



极值点与拐点
一个函数有没有可能存在这样一个点,这个点既是函数的极值点,又是函数的拐点?
对于n阶连续可导函数而言,是绝对不可能的
如果函数在这一点处不可导,那是有可能的,比如分段函数
极值的第三充分条件
对于n阶可导的函数f(x),如果f(x)在某点的前n-1阶导都为0,第n阶导不为0,则若n是偶数,则该点就是f(x)的极值点,若n为奇数,则该点就是f(x)的拐点

假如函数在某一点处不可导,则该点有没有可能是函数的拐点?有没有可能是函数的极值点?
都有可能!因为函数在该点可导并不是在该点取得极值的必要条件,可导也不是拐点的必要条件
极值点的定义:只要函数在该点的某个邻域内的函数值都没有在该点的函数值大,该点就是函数的一个极值点
拐点的定义:只要函数在该点的左右邻域内凹凸性相反(二阶导符号相反),该点就是拐点,不需要函数在该点可导,比如
下面是数分教材中给出的拐点定义






















 1499
1499

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








