首先阐述FM的核心思想:
基于对实对称矩阵的理解,信息的二阶特征Xi和Xj用隐向量的内积表示为:<Vi, Vj>,这里他们是n*k的矩阵,参数量大大降低,也只需要维护Vi一个矩阵即可,本质上Vi和Vj只是转置的关系。
推导公式如下:

公式的不难理解,参考下面的步骤:
【step1】计算说明如下:FM二阶项计算的是下面所有黄色正方形相加之和

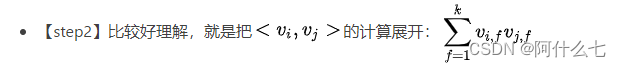

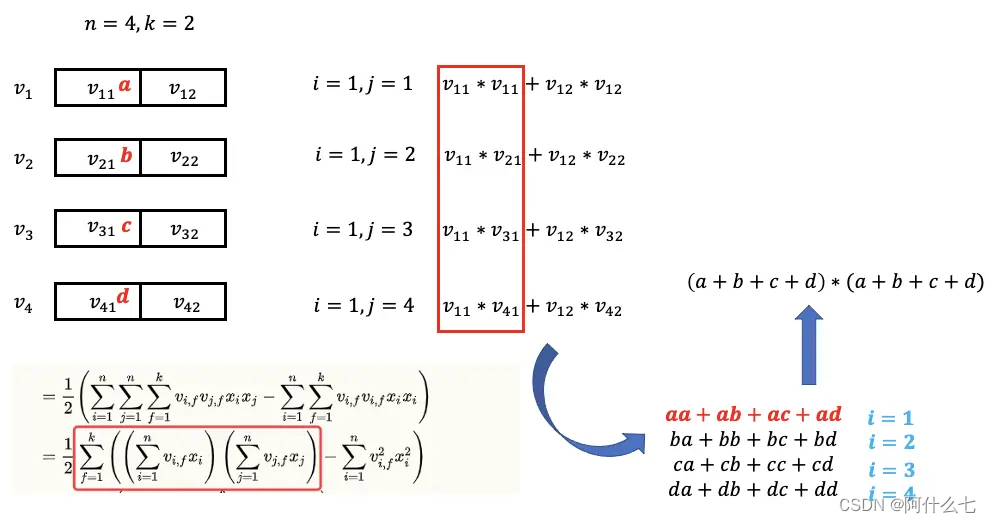
 纠正:第四步骤中,应该从i=1开始,公式错误
纠正:第四步骤中,应该从i=1开始,公式错误
首先阐述FM的核心思想:
基于对实对称矩阵的理解,信息的二阶特征Xi和Xj用隐向量的内积表示为:<Vi, Vj>,这里他们是n*k的矩阵,参数量大大降低,也只需要维护Vi一个矩阵即可,本质上Vi和Vj只是转置的关系。
推导公式如下:

公式的不难理解,参考下面的步骤:
【step1】计算说明如下:FM二阶项计算的是下面所有黄色正方形相加之和

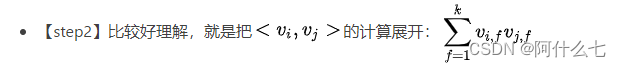


 纠正:第四步骤中,应该从i=1开始,公式错误
纠正:第四步骤中,应该从i=1开始,公式错误
 7799
7799
 6440
6440