涉及到一个数学知识点:prufer定理
Prufer 定理主要包含以下两点:
- n 个节点的无根树(没有指定的根的树,无向无环连通图)可以唯一对应于一个 Prufer 序列,该序列的长度为 n-2
- 不同的 Prufer 序列数量即为不同树的数量,因此: n 个不同节点的树的数量=n^(n-2)
从一棵树生成prufer序列:
- 反复执行以下操作,直到只剩下两个节点:
- 找到编号最小的叶子节点(度数为 1)。
- 记录它的父节点到序列中。
- 删除这个叶子节点。
- 经过 n-2 次操作后,得到一个长度为n-2 的 Prufer 序列(此时树中还剩两个点)
从prufer序列还原回一棵树:
重复进行以下操作,直至点集中只剩下两个点:(初始时所有点都在点集中)
- 取出prufer序列最前面的元素x。
- 取出在点集中的、且当前不在prufer序列中的最小元素y。
- 在x,y之间连接一条边。
最后,我们在点集中剩下的两个点中连一条边。
prufer定理的推论:
Prufer 定理告诉我们,n 个节点的树与一个唯一的 Prufer 序列一一对应,而这个 Prufer 序列的长度为 n-2。
同时,每个节点 i 在 Prufer 序列中出现的次数满足:
count[i]=d_i - 1
其中 d_i 是节点 i 的度数。这意味着:
- 序列总共有 n-2 个数。
- 这些数是从 1,2,.....,n 中选取的,并且每个数 i 在 Prufer 序列中出现d_i - 1 次。
因此,计算满足给定度数分布的不同树的数量,等价于计算满足这些频次限制的 Prufer 序列的数量。
在这个问题中,还要注意判断给定度数能不能构成一棵树:
如果只有一个节点,那这个节点的度数是0
如果有超过一个节点,那没有节点度数是0
节点的度数之和=(n-1)*2,n - 1是边数,每条边贡献两个度数
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
#define ll long long
const int maxn=150+5,N=150;
ll p[maxn][maxn],cnt[maxn],d[maxn];
ll n;
int main()
{
ios::sync_with_stdio(0);cin.tie(0);
cin>>n;
ll sum=0;int flag=1;
for(int i=1;i<=n;i++){
cin>>d[i];
sum+=d[i];
if(d[i]==0 && n!=1) flag=0;
}
if(sum!=(n-1)*2 || flag==0) cout<<0<<"\n";
else {
//预处理出1-150的质因子
for(int i=1;i<=150;i++){
int t=i;
for(int j=2;j<=t;j++){
while(t%j==0){
p[i][j]++;
t/=j;
}
}
}
//先累加分子的质因数
for(int i=1;i<=n-2;i++){
for(int j=2;j<=150;j++){
cnt[j]+=p[i][j];
}
}
//减去分母的质因数
for(int i=1;i<=n;i++){
for(int j=1;j<=d[i]-1;j++){
for(int k=1;k<=150;k++){
cnt[k]-=p[j][k];
}
}
}
//计算答案
ll ans=1;
for(int i=2;i<=150;i++){
ans*=pow(i,cnt[i]);
}
cout<<ans<<"\n";
}
return 0;
}




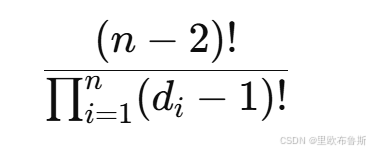
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








