本文介绍了使用二进制的自相似方法解决汉诺塔问题，通过将移动过程与二进制转换对应，展示了如何利用递推关系和基线条件简化盘子移动的逻辑。
这次主要是介绍有趣的解汉诺塔的方法：用二进制的逐渐变大的节奏来求解
我们从0开始，当末尾0变成1时，我们把最上层的0号盘移到它右边的柱子，如果它已经在最右边的柱子上，就把它移到第一根柱子
当我们将末尾01变成10，就移动1号盘（因为有0号盘，所以移到符合规则的位置上）
后面也类似。
下面我用图描述一下整个过程：
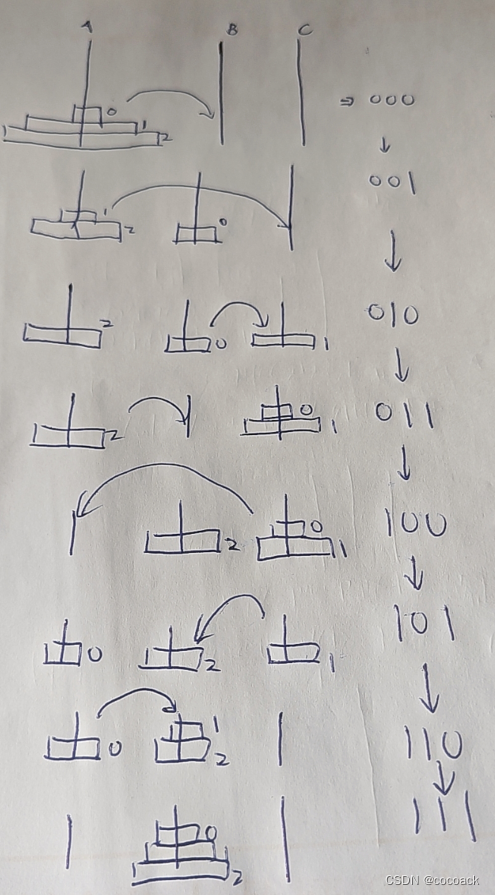
所以，原理是什么呢？
其实，他们的求解是自相似的：比方说，对于圆盘3，它要移动则必须让1，2盘整体移到1柱子，用二进制的视角来说就是为了求100必须先有011，而移动3时相当于011+1变成100，因此我们可以把0变成1的过程与盘子移动联系起来。（或者说，它们基线条件与递推关系一致）
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
