牛顿迭代法

最新推荐文章于 2023-12-31 22:22:12 发布

月疯

最新推荐文章于 2023-12-31 22:22:12 发布

阅读量698

点赞数

分类专栏：【数学】

【数学】专栏收录该内容

54 篇文章

订阅专栏

本文介绍了一种使用牛顿迭代法逼近求解平方根的方法，并通过具体实例展示了算法的实现过程。该方法通过不断迭代逼近目标值，直至达到预设精度。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

其实就是逼近的思想，例如我们要求a的平方根，首先令f(x)=x^2-a，那么我们的目的就是求得x使得f(x)=0，也就是求x^2-a这条曲线与x轴的交点，画图举例：

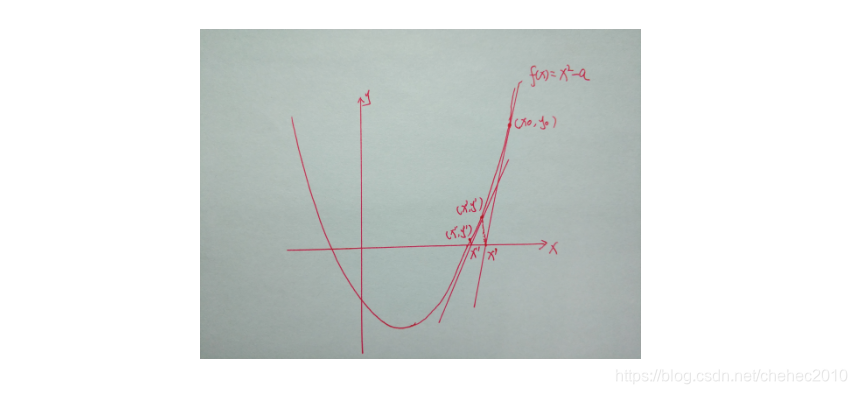
由函数f(x)=x^2-a，我们求导可以知道，函数上任意一点(x,y)的切线的斜率为2x。假设过点（x0,y0）的切线方程为y=kx+b，那么切线与x轴的交点横坐标为-b/k。而b=y0-kx0,k=2x0,y0=x0^2-a,化简-b/k=（x0+a/x0）/2。

也就是说（x0+a/x0）/2是过点（x0,y0）的切线与x轴的交点的横坐标。记（x0+a/x0）/2=x',继续求过点（x',f(x')）的切线与x轴的交点的横坐标x''，很明显x''比x'更靠近函数f(x)=x^2-a与x轴的交点的横坐标(即a的正平方根)。逐渐的逼近f(x)=0;

所以公式为：x' = （x'+a/x'）/2。

代码：

import java.text.DecimalFormat;

public class Main1 {
    public static double sqrt(double x) {  
        if(x<0) {
            return -1;
        }
        //格式化，保证输出位数
        DecimalFormat df = new DecimalFormat("#.00");
        
        double k = x; 
        double precision = 0.000001;
        while((k*k-x)>precision) {
            k=0.5*(k+x/k);  
        }
        return Double.valueOf(df.format(k));
    }
    
    public static void main(String[] args) {
        double a = 9;
        System.out.println(sqrt(a));
    }
}