[USACO1.5] 八皇后 Checker Challenge

[USACO1.5] 八皇后 Checker Challenge

这也是一道经典的深搜题，经典也难：

题目描述

一个如下的 $6\times 6$ 的跳棋棋盘，有六个棋子被放置在棋盘上，使得每行、每列有且只有一个，每条对角线（包括两条主对角线的所有平行线）上至多有一个棋子。

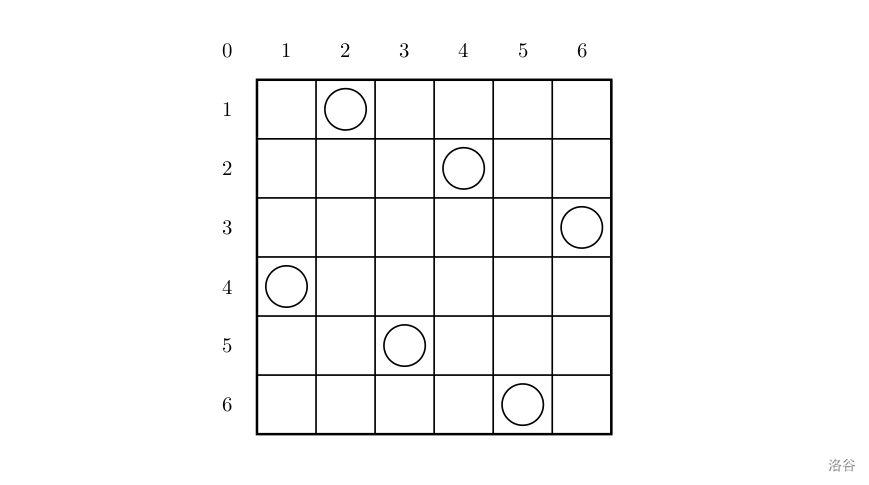
上面的布局可以用序列 $246135$ 来描述，第 $i$ 个数字表示在第 $i$ 行的相应位置有一个棋子，如下：

行号 $123456$

列号 $246135$

这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出，解按字典顺序排列。
请输出前 $3$ 个解。最后一行是解的总个数。

输入格式

一行一个正整数 $n$，表示棋盘是 $n\times n$ 大小的。

输出格式

前三行为前三个解，每个解的两个数字之间用一个空格隔开。第四行只有一个数字，表示解的总数。

输入输出样例 #1

输入 #1

6

输出 #1

2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4

说明/提示

【数据范围】
对于 $100\%$ 的数据，$6\le n\le 13$。

题目翻译来自NOCOW。

USACO Training Section 1.5

看完题目，我们来梳理思路：
这道题虽然和普通的深搜题目相似，但是有一大难点，题目中说要使得每行、每列有且只有一个，每条对角线（包括两条主对角线的所有平行线）上至多有一个棋子，大家看到这应该都会想怎么才能判断对角线上有没有棋子，不急，我们来慢慢找规律：

0	1	2	3	4	5
1	(1,1)	(1,2)	(1,3)	(1,4)	(1,5)
2	(2,1)	(2,2)	(2,3)	(2,4)	(2,5)
3	(3,1)	(3,2)	(3,3)	(3,4)	(3,5)
4	(4,1)	(4,2)	(4,3)	(4,4)	(4,5)
5	(5,1)	(5,2)	(5,3)	(5,4)	(5,5)

我们在这个坐标表格上从右上到左下画一条对角线并记录下经过的每个点的坐标：(1,5)(2,4)(3,3)(4,2)(5,1)
我们根据上面这条坐标串可以发现它的每个点x与y的和都是6，都是相等的，如果想到这一点，那么恭喜你得到了规律。

理论通过，实践少不了，接下来我们来构思代码：
怎样判断对角线上有没有棋子呢？这还是个问题，我们联系深搜的代码基础架构：做标记→递归→还原标记，对角线给了我思路：既然是对角线，那么框架也要“对角起来”。

好了，马上敲代码：

#include<iostream>
using namespace std;
int n,cnt,h[15],l[15],dl[32],dr[32];
void dfs(int x) {
    if (x>n) {
        cnt++;
        if (cnt<=3) {
            for (int i=1;i<=n;i++) {
                cout<<h[i]<<" ";
            }
            cout<<endl;
        }
    }
    for (int i=1;i<=n;i++) {
        if (!l[i] && !dl[i-x+n] && !dr[x+i]) {
            h[x]=i;
            l[i]=1;
            dl[i-x+n]=1;
            dr[x+i]=1;
            dfs(x+1);
            h[x]=0;
            l[i]=0;
            dl[i-x+n]=0;
            dr[x+i]=0;
        }
    }
}
int main() {
    cin>>n;
    dfs(1);
    cout<<cnt<<endl;
    return 0;
}

(第一次在结尾作总结，估计写不出来什么东西）

这道题考察了我们寻找规律和举一反三的能力，也强化了我们对深搜算法的理解。这篇题解到此就结束了，喜欢记得给个点赞，谢谢浏览！