图的存储+遍历_图的存储与遍历练习题-优快云博客

图的存储

大家嚎，今天写到了图，先看图的存储，这里找的例题是洛谷的B3643：

题目

题目描述

给定一个 $n$ 个顶点 $m$ 条边的无向图。请以邻接矩阵和邻接表的形式输出这一张图。

输入格式

第一行输入两个正整数 $n$ 和 $m$ ，表示图的顶点数和边数。

第二行开始，往后 $m$ 行，每行输入两个以空格隔开的正整数 $u, v$ ，表示 $u, v$ 顶点之间有一条边直接相连。

输出格式

首先输出 $n$ 行 $n$ 列的矩阵，以空格隔开每一行之间的数表示邻接矩阵。第 $i$ 行第 $j$ 列的数为 $1$ 则表示顶点 $i, j$ 之间有一条边直接相连；若为 $0$ 则表示没有直接相连的边。

再往后输出 $n$ 行。第 $i$ 行首先先输出一个整数 $d_i$ ，表示这个顶点的度数，再按照从小到大的顺序，依次输出与顶点 $i$ 直接相连的所有顶点。

输入输出样例 #1

输入 #1

输出 #1

说明/提示

样例的图如图所示：

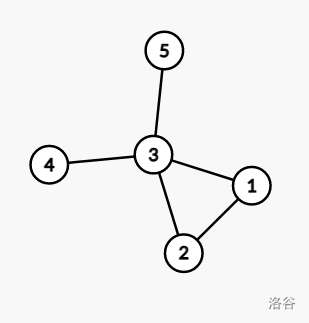
数据保证，对于所有数据， $\leq n \leq 1000$ ， $\leq m \leq 10^5$ ，且图无重边无自环。

解答

分析

这道题题目很好理解（废话，是裸题），看到无向图和矩阵就基本可以是用邻接矩阵做的题了。
大家如果不了解的话可以参考一下邻接矩阵详解，这里我就不做过多的解释了。
很简单，邻接矩阵的基础代码已经解决了两个问题，因为我们可以使用优先队列的自带函数。

答题

根据以上结论我们可以直接得出代码：

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
const int N=1e3+5;
int a[N][N];
vector<int> g[N];
int main() {
    int n,m;
    cin>>n>>m;
    for(int x,y,i=1;i<=m;i++) {
        cin>>x>>y;
        a[x][y]=a[y][x]=1;
        g[x].push_back(y);
        g[y].push_back(x);
    }
    for (int i=1;i<=n;i++) {
        for (int j=1;j<=n;j++) {
            cout<<a[i][j]<<" ";
        }
        cout<<endl;
    }
    for (int i=1;i<=n;i++) {
        cout<<g[i].size()<<' ';
        sort(g[i].begin(),g[i].end());
        for (int j=0;j<g[i].size();j++) {
            cout<<g[i][j]<<' ';
        }
        cout<<endl;
    }
    return 0;
}

图的存储部分到此结束。

图的遍历

上面讲完了图的存储，但是图的存储方式不止邻接矩阵一种，还有邻接表和链式前向星，这一部分我们都会用到。接下来我们继续来看图的遍历，这里找的例题是洛谷的U279163：

题目

题目描述

给出一有向图，包含n个点，编号从1-n，m条边，询问是否能从a点走到b点？

输入格式

第一行4个整数n,m,a,b 接下来m行，每行2个整数x，y，表示x到y有一条有向边

输出格式

如果能走到输出Yes，否则输出No

输入输出样例 #1

输入 #1

3 2 1 3
1 2
2 3

输出 #1

Yes

输入输出样例 #2

输入 #2

3 2 1 3
1 2
2 1

输出 #2

No

说明/提示

$0 < n, m <= 200000, a, b, x, y 保证合法$

解答

分析

这道题很基础，图的遍历主要用到的是优先搜索，包括广度优先搜索和深度优先搜索，我在这道题会用两种方法进行解答。

答题

1.深度优先搜索+链式前向星：

#include<iostream>
using namespace std;
const int N=2e5+5,M=2e5+5;
int vis[N],h[N],cnt,n,m,a,b;
struct edge {
    int to,next;
} e[M];
void add(int x,int y) {
    cnt++;
    e[cnt].to=y;
    e[cnt].next=h[x];
    h[x]=cnt;
}
void dfs(int s) {
    vis[s]=1;
    for (int i=h[s];i!=0;i=e[i].next) {
        if (!vis[e[i].to]) {
            vis[e[i].to]=1;
            dfs(e[i].to);
        }
    }
}
int main() {
    cin>>n>>m>>a>>b;
    for (int x,y,i=0;i<m;i++) {
        cin>>x>>y;
        add(x,y);
    }
    dfs(a);
    if (vis[b]) {
        cout<<"Yes";
    }else {
        cout<<"No";
    }
    return 0;
}

2.广度优先搜索+邻接表：

#include<iostream>
#include<vector>
#include<queue>
using namespace std;
const int N=2e5+5,M=2e5+5;
vector<int> g[N];
int vis[N],n,m,a,b;
void bfs(int s) {
    queue<int> q;
    q.push(s);
    vis[s]=1;
    while (!q.empty()) {
        int t=q.front();
        q.pop();
        for (int i=0;i<g[t].size();i++) {
            if (!vis[g[t][i]]) {
                vis[g[t][i]]=1;
                q.push(g[t][i]);
            }
        }
    }
}
int main() {
    cin>>n>>m>>a>>b;
    for (int x,y,i=0;i<m;i++) {
        cin>>x>>y;
        g[x].push_back(y);
    }
    bfs(a);
    if (vis[b]) {
        cout<<"Yes";
    }else {
        cout<<"No";
    }
    return 0;
}