【Python例程】集合卡尔曼滤波（EnKF）在Lorenz63混沌系统中的状态估计仿真，附工程的下载链接

这段代码实现了集合卡尔曼滤波（Ensemble Kalman Filter, EnKF）在Lorenz 63混沌系统中的状态估计仿真。通过将随机扰动的集合成员作为样本，EnKF在非线性动力系统中实现了对真实状态的逐步逼近。

代码介绍

系统模型

使用 Lorenz 63 混沌系统 作为状态演化模型，其连续形式为：

$$\{\begin{array}{l}\dot{x}=\sigma (y-x)\dot{y}=x(\rho -z)-y\dot{z}=xy-\beta z\end{array}$$

其中：

• $\sigma$、$\rho$、$\beta$为系统参数；
• 状态向量为$\mathbf{x}=[x,y,z{]}^T$。

离散化后使用四阶 Runge-Kutta 积分方法，并叠加小的高斯噪声来模拟模型误差。

观测模型

观测算子定义为仅测量 (x) 与 (y) 分量：
$${\mathbf{z}}_k=H{\mathbf{x}}_k+{\mathbf{v}}_k,$$
其中$H=\left[\begin{array}{ccccc}1& 0& 00& 1& 0\end{array}\right]$，
观测噪声${\mathbf{v}}_k\sim \mathcal{N}(0,R)$。

EnKF滤波过程

1. 初始化集合：
   $$X_0^{(i)}\sim \mathcal{N}({\mathbf{x}}_0,P_0),i=1,\dots ,N$$

2. 预测步骤（Forecast）：
   对每个集合成员应用系统模型：
   $$X_k^{(i)-}=f(X_{k-1}^{(i)})$$

3. 分析步骤（Analysis）：
   计算预测观测：
   $$Y_k^{(i)}=h(X_k^{(i)-})$$
   然后根据样本协方差估计卡尔曼增益：
   $$K_k=P_{xy}(P_{yy}+R{)}^{-1}$$
   并更新每个集合成员：
   $$X_k^{(i)}=X_k^{(i)-}+K_k[z_k+{ϵ}^{(i)}-Y_k^{(i)}]$$
   其中${ϵ}^{(i)}\sim \mathcal{N}(0,R)$为观测扰动。

代码结构说明

模块	功能
EnsembleKalmanFilter 类	实现EnKF的核心结构，包括初始化、预测、分析、均值与协方差计算
lorenz63_model()	Lorenz系统的状态演化函数（含Runge-Kutta积分）
observation_operator()	定义观测关系，仅输出状态的前两维
主程序部分	完成数据生成、滤波执行与结果可视化

文件列表：

运行结果

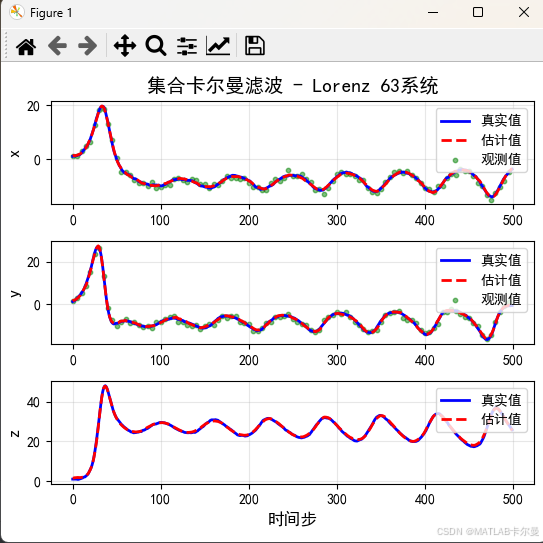
滤波前后状态曲线：

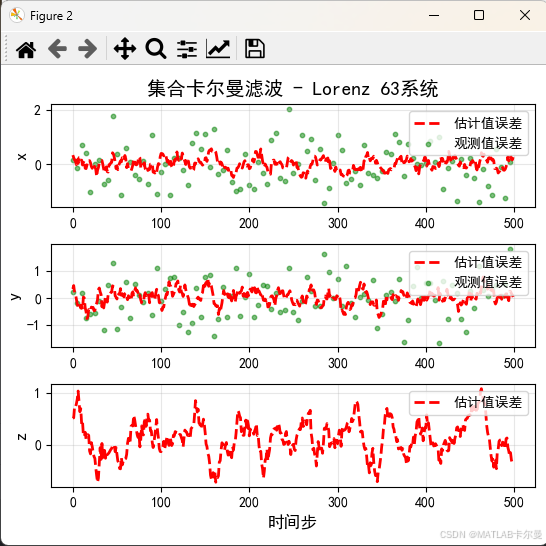
滤波前后误差曲线：

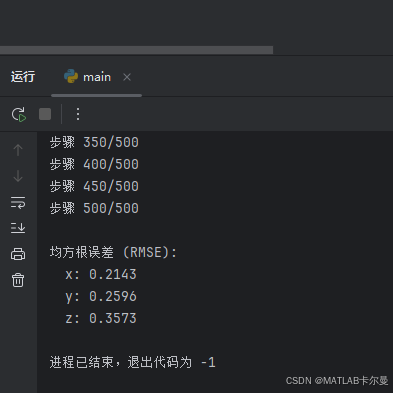
运行结果：

运行录屏：

【Python例程】集合卡尔曼滤波（EnKF）

代码获取

完整代码（工程）的下载链接：
https://download.youkuaiyun.com/download/callmeup/92292131

或：
如需帮助，或有导航、定位滤波相关的代码定制需求，请点击下方卡片联系作者