【MATLAB绘图进阶教程】（4-1）科学视图（等值线图、三维矢量场流场模拟、曲面拟合与插值）

原创 于 2025-09-11 10:11:25 发布 · 223 阅读 · 0 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#matlab #绘图 #等值线图 #矢量场图

在这里插入图片描述

本教程介绍MATLAB中三个核心的科学可视化技术：等值线图、三维矢量场流场模拟以及曲面拟合与插值可视化。

文章目录

等值线图与等高线

等值线图是表示二维标量场的有效方法，广泛应用于地形图、温度分布、压力场等科学领域的可视化。

基本概念

  • 等值线（contour）：连接具有相同数值的点形成的曲线
  • 等高线：特指地形高度的等值线
  • 等值面填充：在等值线之间填充颜色以增强视觉效果

contour函数：线条等值线图

contour函数用于绘制等值线，语法格式：

contour(X, Y, Z, levels)

基础示例：二元函数的等值线

figure;
% 创建网格
[X, Y] = meshgrid(-3:0.1:3, -3:0.1:3);

% 定义二元函数：高斯函数
Z = exp(-(X.^2 + Y.^2));

% 绘制等值线图
figure;
contour(X, Y, Z, 15);  % 15条等值线
colorbar;
xlabel('X');
ylabel('Y');
title('高斯函数等值线图');
grid on;

运行结果：

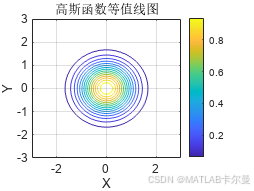
在这里插入图片描述

进阶应用：自定义等值线数值

figure;
% 指定特定等值线数值
levels = [0.1, 0.3, 0.5, 0.7, 0.9];
[C, h] = contour(X, Y, Z, levels);
clabel(C, h, 'FontSize', 12);  % 添加数值标签
colorbar;
title('自定义等值线数值');

运行结果：
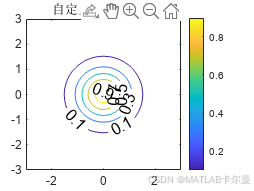
在这里插入图片描述

contourf函数：填充等值线图

contourf函数在等值线之间填充颜色，提供更直观的视觉效果：

figure;
% 创建更复杂的函数进行演示
[X, Y] = meshgrid(-2:0.05:2, -2:0.05:2);
Z = sin(X) .* cos(Y) + 0.1 * (X.^2 + Y.^2);

contourf(X, Y, Z, 20);  % 20个填充级别
colorbar;
xlabel('X');
ylabel('Y');
title('填充等值线图：sin(x)cos(y) + 0.1(x² + y²)');
colormap(jet);  % 设置颜色映射

运行结果：
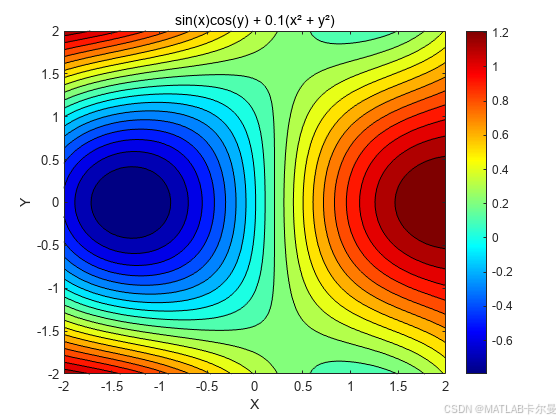
在这里插入图片描述

地形图模拟示例

% 模拟山地地形
[X, Y] = meshgrid(-10:0.2:10, -10:0.2:10);
Z1 = 50 * exp(-((X-2).^2 + (Y-2).^2)/8);      % 山峰1
Z2 = 30 * exp(-((X+3).^2 + (Y-1).^2)/12);     % 山峰2
Z3 = 40 * exp(-(X.^2 + (Y+3).^2)/15);         % 山峰3
Z = Z1 + Z2 + Z3 + 5;  % 基础海拔

figure;
subplot(1,2,1);
contour(X, Y, Z, 15);
colorbar;
title('地形等高线图');
xlabel('X (km)');
ylabel('Y (km)');
grid on;

subplot(1,2,2);
contourf(X, Y, Z, 20);
colorbar;
title('地形填充图');
xlabel('X (km)');
ylabel('Y (km)');

运行结果：
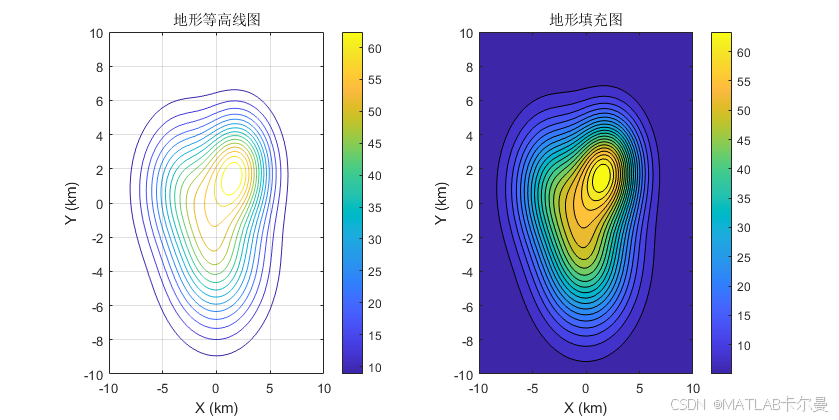
在这里插入图片描述

三维矢量场与流场模拟

矢量场可视化是计算流体力学（CFD）中的重要技术，用于显示速度场、电磁场等矢量数据。

基本矢量场可视化

二维矢量场：quiver函数

% 创建二维网格
[X, Y] = meshgrid(-2:0.3:2, -2:0.3:2);

% 定义矢量场：旋转场
U = -Y;              % X方向分量
V = X;               % Y方向分量

figure;
quiver(X, Y, U, V, 'b');
axis equal;
xlabel('X');
ylabel('Y');
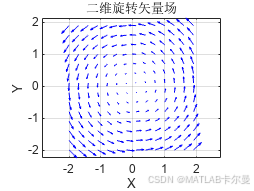
title('二维旋转矢量场');
grid on;

运行结果：
在这里插入图片描述

三维矢量场：quiver3函数

% 创建三维网格
[X, Y, Z] = meshgrid(-1:0.4:1, -1:0.4:1, -1:0.4:1);

% 定义三维矢量场：螺旋场
U = -Y;
V = X;
W = 0.5 * Z;

figure;
quiver3(X, Y, Z, U, V, W, 0.5);
xlabel('X');
ylabel('Y');
zlabel('Z');
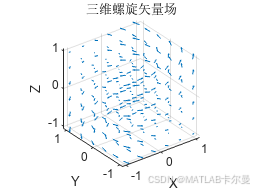
title('三维螺旋矢量场');
axis equal;
grid on;

运行结果：

在这里插入图片描述

流场模拟案例

案例1：圆柱体绕流

% 圆柱体绕流模拟（势流近似）
[X, Y] = meshgrid(-3:0.15:3, -2:0.15:2);

% 圆柱体参数
cylinder_radius = 0.5;
U_inf = 1;  % 来流速度

% 计算距离
R = sqrt(X.^2 + Y.^2);
theta = atan2(Y, X);

% 势流解（无粘性近似）
% 避免圆柱体内部计算
mask = R > cylinder_radius;

U = zeros(size(X));
V = zeros(size(Y));

% 只在圆柱体外部计算速度场
U(mask) = U_inf * (1 - (cylinder_radius^2) ./ (R(mask).^2)) .* (1 + cos(2*theta(mask)));
V(mask) = -U_inf * (cylinder_radius^2) ./ (R(mask).^2) .* sin(2*theta(mask));

% 绘制流场
figure;
% 绘制流线
streamslice(X, Y, U, V);
hold on;

% 绘制圆柱体
theta_circle = 0:0.1:2*pi;
x_circle = cylinder_radius * cos(theta_circle);
y_circle = cylinder_radius * sin(theta_circle);
fill(x_circle, y_circle, 'k');

axis equal;
xlim([-3 3]);
ylim([-2 2]);
xlabel('X');
ylabel('Y');
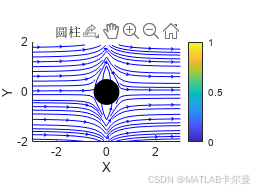
title('圆柱体绕流流线图');
colorbar;

运行结果：

在这里插入图片描述

案例2：涡旋流场

% 双涡旋相互作用
[X, Y] = meshgrid(-4:0.2:4, -4:0.2:4);

% 涡旋参数
gamma1 = 10;   % 涡旋1强度
gamma2 = -8;   % 涡旋2强度（反向）
x1 = -1; y1 = 0;   % 涡旋1位置
x2 = 1; y2 = 0;    % 涡旋2位置

% 计算距离
R1 = sqrt((X-x1).^2 + (Y-y1).^2);
R2 = sqrt((X-x2).^2 + (Y-y2).^2);

% 避免奇点
R1(R1 < 0.1) = 0.1;
R2(R2 < 0.1) = 0.1;

% 计算速度场
U1 = -gamma1 * (Y-y1) ./ (2*pi * R1.^2);
V1 = gamma1 * (X-x1) ./ (2*pi * R1.^2);

U2 = -gamma2 * (Y-y2) ./ (2*pi * R2.^2);
V2 = gamma2 * (X-x2) ./ (2*pi * R2.^2);

U = U1 + U2;
V = V1 + V2;

figure;
% 绘制速度大小的填充图
speed = sqrt(U.^2 + V.^2);
contourf(X, Y, speed, 20);
colorbar;
hold on;

% 叠加流线
streamslice(X, Y, U, V, 2);
xlabel('X');
ylabel('Y');
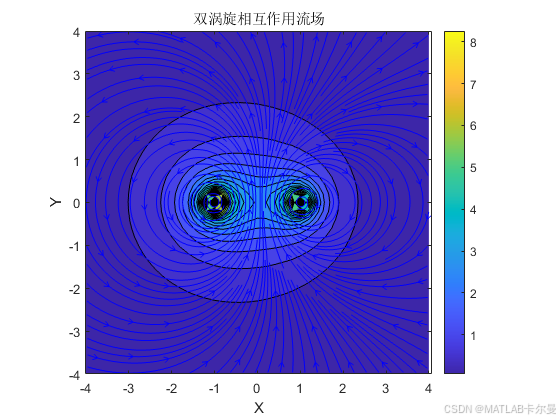
title('双涡旋相互作用流场');
axis equal;

运行结果：

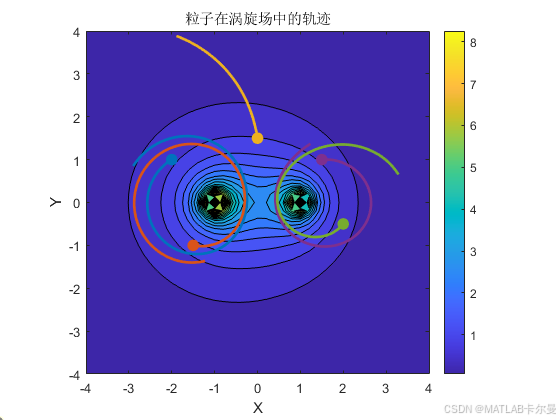
在这里插入图片描述

粒子轨迹追踪

% 在涡旋场中追踪粒子轨迹
% 使用前面定义的涡旋流场

% 初始粒子位置
x0 = [-2, -1.5, 0, 1.5, 2];
y0 = [1, -1, 1.5, 1, -0.5];

figure;
contourf(X, Y, speed, 20);
colorbar;
hold on;

% 为每个粒子计算轨迹
dt = 0.05;
t_final = 10;
time = 0:dt:t_final;

colors = lines(length(x0));

for i = 1:length(x0)
    x_traj = zeros(size(time));
    y_traj = zeros(size(time));
    x_traj(1) = x0(i);
    y_traj(1) = y0(i);
    
    for j = 2:length(time)
        % 插值获取当前位置的速度
        u_interp = interp2(X, Y, U, x_traj(j-1), y_traj(j-1), 'linear', 0);
        v_interp = interp2(X, Y, V, x_traj(j-1), y_traj(j-1), 'linear', 0);
        
        % 更新位置（欧拉法）
        x_traj(j) = x_traj(j-1) + u_interp * dt;
        y_traj(j) = y_traj(j-1) + v_interp * dt;
    end
    
    % 绘制轨迹
    plot(x_traj, y_traj, 'Color', colors(i,:), 'LineWidth', 2);
    plot(x0(i), y0(i), 'o', 'Color', colors(i,:), 'MarkerSize', 8, 'MarkerFaceColor', colors(i,:));
end

xlabel('X');
ylabel('Y');
title('粒子在涡旋场中的轨迹');
axis equal;
xlim([-4 4]);
ylim([-4 4]);

运行结果：
在这里插入图片描述

曲面拟合与插值可视化

在实验数据处理和数值分析中，经常需要从散乱的数据点重构连续的曲面。

griddata函数：散点插值

griddata函数可以将散乱分布的数据插值到规则网格上。

基本语法：

Zi = griddata(x, y, z, Xi, Yi, method)

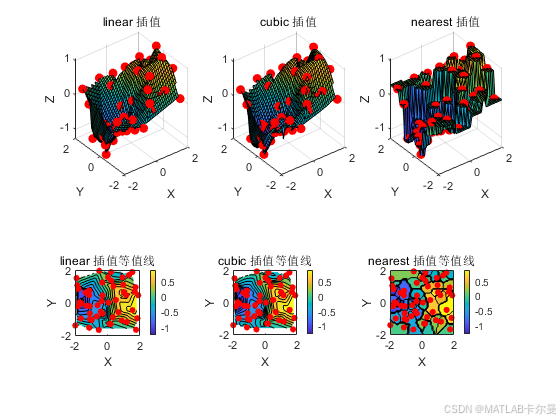
基础示例：随机数据插值

% 生成随机散点数据
n = 50;
x = 4 * rand(n, 1) - 2;  % [-2, 2]范围内随机点
y = 4 * rand(n, 1) - 2;
z = sin(x) .* cos(y) + 0.2 * randn(n, 1);  % 添加噪声

% 创建规则网格用于插值
[Xi, Yi] = meshgrid(-2:0.1:2, -2:0.1:2);

% 不同插值方法比较
methods = {'linear', 'cubic', 'nearest'};

figure;
for i = 1:3
    subplot(2, 3, i);
    Zi = griddata(x, y, z, Xi, Yi, methods{i});
    surf(Xi, Yi, Zi);
    hold on;
    plot3(x, y, z, 'ro', 'MarkerSize', 6, 'MarkerFaceColor', 'r');
    title([methods{i} ' 插值']);
    xlabel('X'); ylabel('Y'); zlabel('Z');
    
    subplot(2, 3, i+3);
    contourf(Xi, Yi, Zi, 15);
    hold on;
    plot(x, y, 'ro', 'MarkerSize', 4, 'MarkerFaceColor', 'r');
    colorbar;
    title([methods{i} ' 插值等值线']);
    xlabel('X'); ylabel('Y');
    axis equal;
end

运行结果：

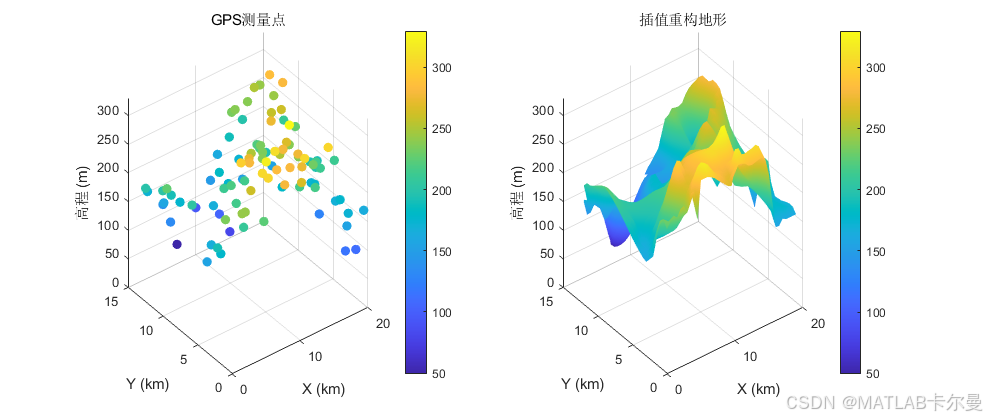
在这里插入图片描述

实际应用：地形数据插值

% 模拟GPS测量的地形高程数据
n_points = 100;
x_measure = 20 * rand(n_points, 1);  % [0, 20] km
y_measure = 15 * rand(n_points, 1);  % [0, 15] km

% 模拟地形：多个山丘
z_measure = 200 + 100 * sin(x_measure/5) .* cos(y_measure/4) + ...
            50 * exp(-((x_measure-10).^2 + (y_measure-7).^2)/20) + ...
            30 * randn(n_points, 1);  % 测量误差

% 创建高分辨率网格
[Xi, Yi] = meshgrid(0:0.5:20, 0:0.5:15);

% 三次插值
Zi = griddata(x_measure, y_measure, z_measure, Xi, Yi, 'cubic');

figure;
subplot(1, 2, 1);
scatter3(x_measure, y_measure, z_measure, 50, z_measure, 'filled');
colorbar;
xlabel('X (km)'); ylabel('Y (km)'); zlabel('高程 (m)');
title('GPS测量点');

subplot(1, 2, 2);
surf(Xi, Yi, Zi);
colorbar;
xlabel('X (km)'); ylabel('Y (km)'); zlabel('高程 (m)');
title('插值重构地形');
shading interp;

运行结果：

在这里插入图片描述

scatteredInterpolant类：高效插值

scatteredInterpolant是MATLAB中更现代和高效的散点插值工具，特别适合大数据集。

基本用法：

% 使用scatteredInterpolant进行插值
n = 200;
x = 6 * rand(n, 1) - 3;
y = 6 * rand(n, 1) - 3;
z = peaks(x, y) + 0.1 * randn(n, 1);  % 使用peaks函数加噪声

% 创建插值对象
F = scatteredInterpolant(x, y, z, 'linear', 'nearest');

% 生成查询网格
[Xq, Yq] = meshgrid(-3:0.1:3, -3:0.1:3);
Zq = F(Xq, Yq);

figure;
subplot(1, 2, 1);
scatter(x, y, 50, z, 'filled');
colorbar;
xlabel('X'); ylabel('Y');
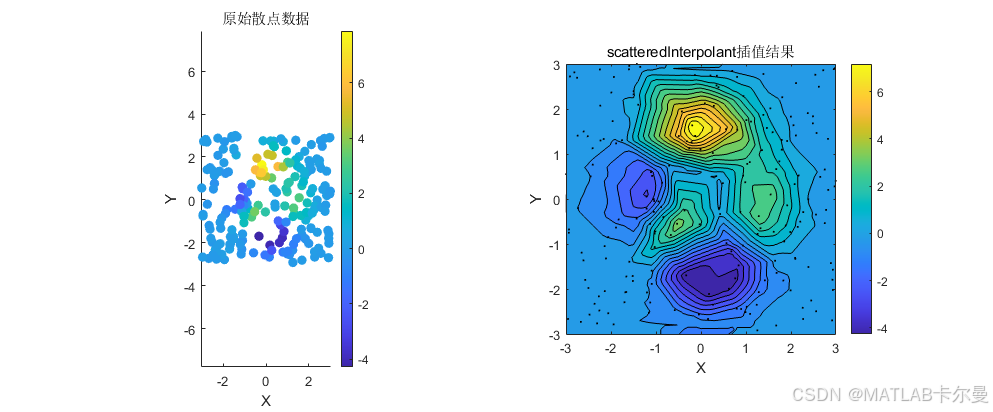
title('原始散点数据');
axis equal;

subplot(1, 2, 2);
contourf(Xq, Yq, Zq, 20);
hold on;
plot(x, y, 'k.', 'MarkerSize', 4);
colorbar;
xlabel('X'); ylabel('Y');
title('scatteredInterpolant插值结果');
axis equal;

运行结果：
在这里插入图片描述

例程文件

上述例程汇总的mlx文件下载链接：
https://download.youkuaiyun.com/download/callmeup/91914095
下载后运行即可得到上面的结果。

如需帮助，或有导航、定位滤波相关的代码定制需求，请点击下方卡片联系作者

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

MATLAB卡尔曼

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值