限时免费【matlab代码】层次聚类（Hierarchical Clustering）的代码例程

市面上很多商家用一些小玩意来卖钱，简单的例子却卖了很高的价格，甚至几十块的程序无法跑通、兼容性问题无法解决等。这里将一些小例子免费分享给大家。
如果觉得不错，欢迎订阅我的其他付费专栏：

• MATLAB定位与滤波例程：https://blog.youkuaiyun.com/callmeup/category_12916974.html
• MATLAB定位程序与详解：https://blog.youkuaiyun.com/callmeup/category_12794805.html
• IMM交互式多模型滤波MATLAB实践：https://blog.youkuaiyun.com/callmeup/category_12816762.html

本文所述的程序实现了层次聚类（Hierarchical Clustering）的操作分析。二维数据集，并使用MATLAB中的linkage和cluster函数进行层次聚类分析。最终，程序会输出每个簇的大小、每个簇的聚类误差，并绘制树状图、聚类前的数据分布和聚类后的结果。

运行结果

层次结构示意图：

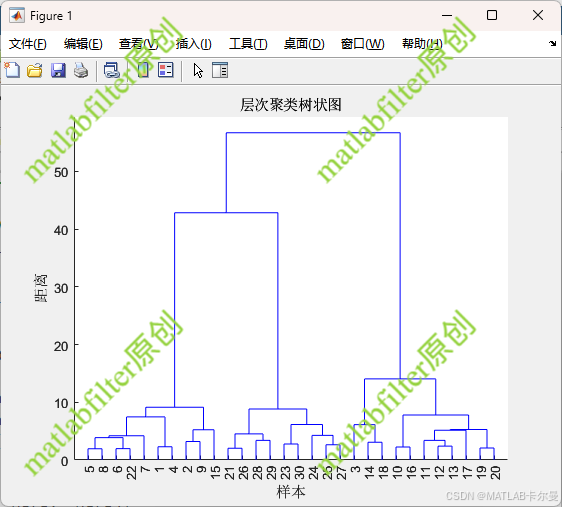
待聚类数据：

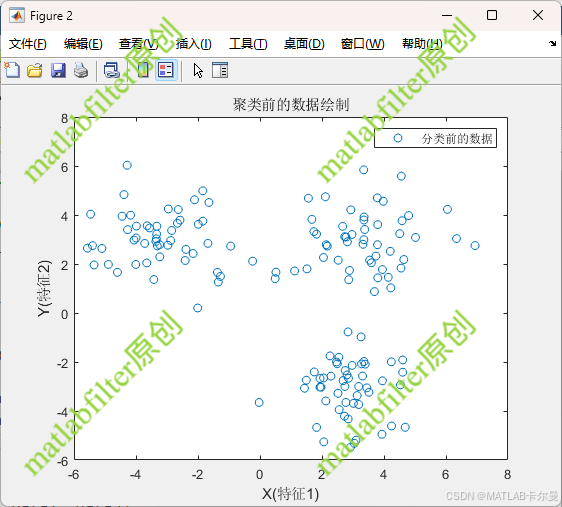
聚类后的结果：

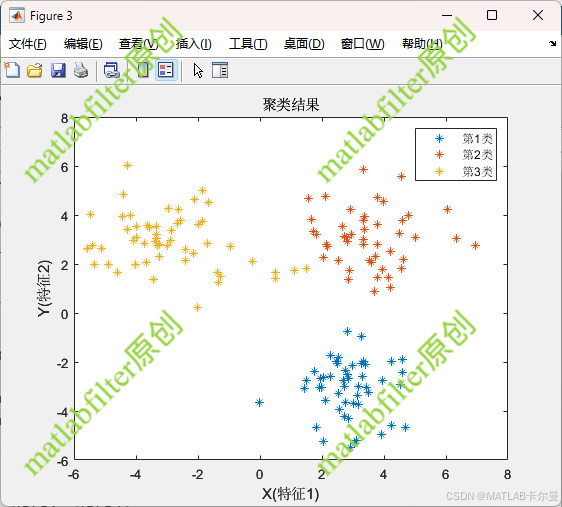
命令行输出的结果：

MATLAB源代码

程序结构：

部分代码：

%% 层次聚类（Hierarchical Clustering）
% 2025-06-29/Ver1
clear; clc; close all;
rng(0); % 固定随机种子，确保结果可重现

%% 生成数据
% 数据点数
numPoints = 200;
% 生成示例数据
data1 = 1.1*randn(numPoints/4, 2) + [3, 3];
data2 = 1.2*randn(numPoints/4, 2) + [-3, 3];
data3 = randn(numPoints/4, 2) + [3, -3];

% 合并数据
data = [data1; data2; data3];
%% 计算
% 计算距离矩阵
distances = pdist(data);
% 进行层次聚类
Z = linkage(distances, 'ward'); % 使用Ward方法
% 进行聚类并指定簇的数量
T = cluster(Z, 'maxclust', 3); % 指定3个簇

完整代码下载链接：https://download.youkuaiyun.com/download/callmeup/91201771

程序详解

在这段程序中，层次聚类的核心原理涉及到距离计算、聚类过程和聚类误差的计算。以下是与本程序相关的算法要点和核心公式：

距离计算（Euclidean Distance）

层次聚类算法需要计算数据点之间的距离，这里使用的是欧氏距离。假设有两个数据点 $x=[x_1,x_2,...,x_d]$ 和 $y=[y_1,y_2,...,y_d]$，它们在 $d$ 维空间中的欧氏距离公式为：

$$d(x,y)=\sqrt{\sum _{i=1}^d(x_i-y_i{)}^2}$$

该公式计算的是两个点之间的直线距离，常用于度量数据点之间的相似度。

层次聚类中的合并方法

在层次聚类中，簇的合并是根据某种准则进行的。常见的合并方法有：单链接（Single Linkage）、完全链接（Complete Linkage）、平均链接（Average Linkage）和Ward方法（Ward’s Method）。

Ward方法（用于本程序）：

Ward方法是一种最小化簇内方差的合并策略，它的核心思想是选择将合并后的簇的方差增量最小的两个簇进行合并。

假设有两个簇 $A$ 和 $B$，它们的总方差 $S_{total}$ 在合并前的方差为：

$$S_{total}=S_A+S_B$$

合并后的簇的方差 $S_{AB}$ 计算为：

$$S_{AB}=\frac{n_A{n}_B}{n_A+n_B}\cdot ({\mu }_A-{\mu }_B{)}^2$$

其中：

• $S_A$ 和 $S_B$ 分别是簇 $A$ 和 $B$ 的方差。
• $n_A$ 和 $n_B$ 是簇 $A$ 和 $B$ 的数据点数量。
• ${\mu }_A$ 和 ${\mu }_B$ 分别是簇 $A$ 和 $B$ 的均值（质心）。

合并过程选择的是使方差增量最小的簇对。合并后的簇会朝着这两个簇的均值中心移动。

其他合并方法：

• 单链接（Single Linkage）：两个簇的距离由它们之间最近的两个点之间的距离来决定。

  d ( A , B ) = min ⁡ { d ( x , y ) ∣ x ∈ A , y ∈ B } d(A, B) = \min \{d(x, y) | x \in A, y \in B \} d(A,B)=min{d(x,y)∣x∈A,y∈B}

• 完全链接（Complete Linkage）：两个簇的距离由它们之间最远的两个点之间的距离来决定。

  d ( A , B ) = max ⁡ { d ( x , y ) ∣ x ∈ A , y ∈ B } d(A, B) = \max \{d(x, y) | x \in A, y \in B \} d(A,B)=max{d(x,y)∣x∈A,y∈B}

• 平均链接（Average Linkage）：两个簇的距离是簇内所有点对的平均距离。

  $$d(A,B)=\frac{1}{|A|\cdot |B|}\sum _{x\in A,y\in B}d(x,y)$$

聚类误差的计算

聚类误差通常使用每个簇内部数据点与簇中心（均值）之间的距离来衡量。假设簇 $i$ 的所有点集合为 $C_i$，簇中心为 ${\mu }_i$，那么簇的误差可以表示为簇内数据点到簇中心的平均距离：

$${\text{误差}}_i=\frac{1}{|C_i|}\sum _{x\in C_i}d(x,{\mu }_i)$$

其中：

• $|C_i|$ 是簇 $i$ 中的数据点数。
• $d(x,{\mu }_i)$ 是数据点 $x$ 到簇中心 ${\mu }_i$ 的距离。

如果聚类效果很好，误差值应该较小；如果误差较大，表示聚类效果较差，簇之间的分隔不明显。

聚类误差的总和

对于所有的簇，聚类的总体误差是每个簇误差的加权平均，或者简单地就是所有簇误差的总和：

$$\text{总误差}=\sum _{i=1}^k{\text{误差}}_i$$

其中 $k$ 是簇的数量，通常是预先设定的（在程序中为3个簇）。

树状图的高度

树状图（dendrogram）展示了聚类的合并过程。树的高度表示了合并两个簇的相似度，合并时的距离越大，树状图的高度也越高。每个节点的高度代表了该节点对应的簇合并时的距离值。

$$\text{高度}=d(A,B)$$

其中 $A$ 和 $B$ 是合并的两个簇，$d(A,B)$ 是它们之间的距离。

如需帮助，或有导航、定位滤波相关的代码定制需求，请点击下方卡片联系作者