【MATLAB例程】GMM聚类算法演示代码，包括生成模拟数据、簇数选择、模型训练、结果可视化，性能评估等，附代码下载链接

GMM聚类算法演示代码，包括生成模拟数据、簇数选择、模型训练、结果可视化，性能评估等，输出多个图示和文字性结果。

功能概述

代码实现基于高斯混合模型（$GaussianMixtureModel,GMM$）的聚类算法，完整展示从数据生成、模型选择、GMM训练到结果评估与可视化的流程。

1. 数据生成：
   通过设定均值向量 μ 和协方差矩阵 Σ，生成服从多元高斯分布的数据：

   • 公式：
     $$p(x|\mu ,\Sigma )=\frac{1}{(2\pi {)}^{d/2}|\Sigma {|}^{1/2}}\exp \left(-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )\right)$$
     其中，$d$ 为特征维度。

2. 簇数选择：
   使用贝叶斯信息准则（BIC）评估不同簇数的模型，选择最优簇数：

   • 公式：
     $$\text{BIC}=-2\ln (L)+k\ln (n)$$
     其中，$L$ 为模型的最大似然估计，$k$ 为模型参数数目，$n$ 为样本数。

3. GMM模型训练：
   使用期望最大化算法（EM）拟合混合高斯模型，估计每个样本属于各簇的后验概率：

   • 后验概率公式：
     $$p(z=k|x)=\frac{{\pi }_k\cdot p(x|{\mu }_k,{\Sigma }_k)}{{\sum }_{j=1}^K{\pi }_j\cdot p(x|{\mu }_j,{\Sigma }_j)}$$
     其中，${\pi }_k$ 是第 $k$ 个高斯分布的权重。

4. 性能评估与可视化：

   • 使用轮廓系数衡量聚类效果：
     $$S=\frac{b-a}{\max (a,b)}$$
     其中，$a$ 为样本点与同簇内其他点的平均距离，$b$ 为样本点与最近簇的平均距离。
   • 绘制数据分布、决策边界、BIC曲线及后验概率分布。

执行代码后可获得：

1. 原始数据分布：通过真实标签标注的二维数据。
2. BIC曲线：展示不同簇数对应的 BIC 值，确定最优簇数。
3. GMM聚类结果：带决策边界的聚类可视化。
4. 后验概率分布：样本属于各簇的概率分布。
5. 轮廓系数：评估聚类效果，取值范围为 $[-1,1]$，越接近 $1$ 越好。

运行结果

原始数据：

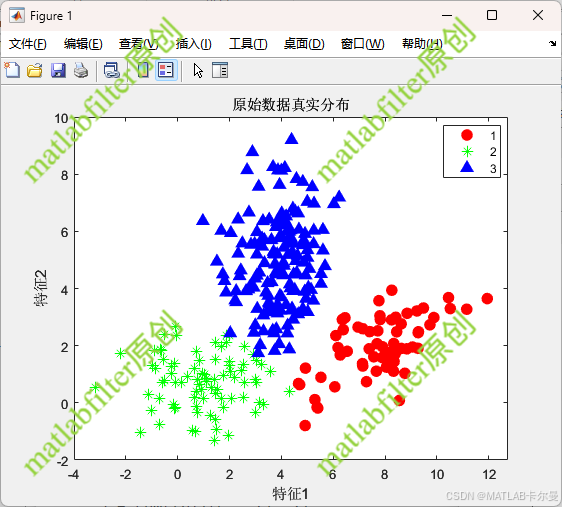
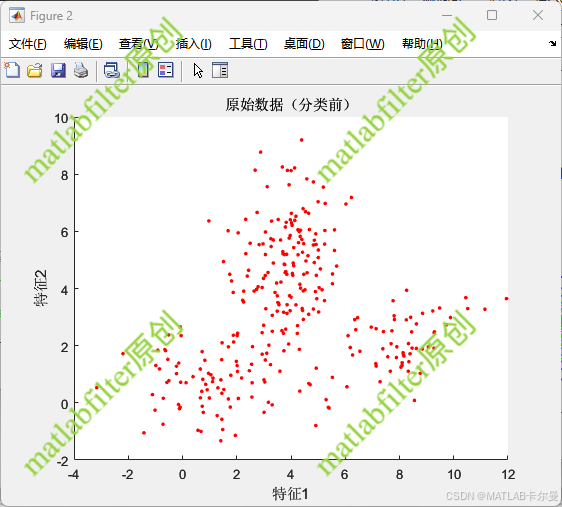
聚类后的结果如下：

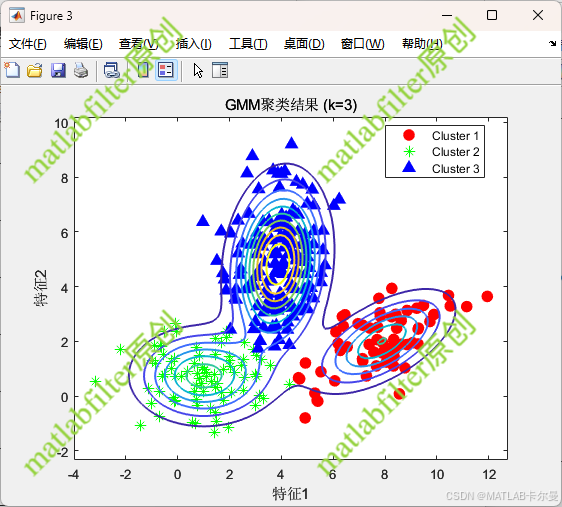
簇数与BIC之间的关系（BIC值最小的簇数即为最佳数）：

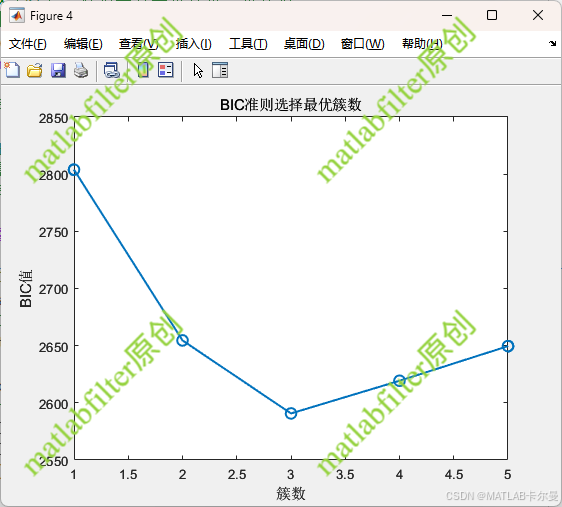
matlab源代码

程序结构：

部分代码如下：

%% GMM聚类算法演示，包括生成模拟数据、簇数选择、模型训练、结果可视化、性能评估等
% 2025-06-25/Ver1
clear; clc; close all;
rng(0); % 固定随机种子，确保结果可重现

%% 合成数据生成（二维示例）
mu_true = [1 1; 4 5; 8 2];     % 设置真实均值矩阵（3簇）
sigma_true = cat(3, [2 0;0 1], [1 0;0 3], [2 0.5;0.5 1]); % 生成真实协方差矩阵（三簇的协方差矩阵）
n_samples = 300;                % 总样本数
proportions = [0.3, 0.5, 0.2];  % 各簇的样本比例

% 检查比例是否正确，保证比例之和为1

完整代码的下载链接：https://download.youkuaiyun.com/download/callmeup/91200955

如需帮助，或有导航、定位滤波相关的代码定制需求，请点击下方卡片联系作者