【MATLAB例程】制导方法介绍与例程——三点法|三维空间，动态目标导引（附源代码下载链接）

代码利用三角定位和动态调整，实时更新导弹的飞行路径，以提高命中率，广泛应用于军事导弹和无人机等领域。`

代码说明

• 参数配置
  明确分离制导站坐标、目标运动参数和导弹性能参数，便于修改场景。

• 运动学更新
  每个时间步动态计算目标新位置，并根据当前雷达-目标连线方向修正导弹航向，确保严格遵循三点法规则。

• 可视化增强
  使用三维箭头标注初始瞄准线，区分目标和导弹轨迹线型，直观展示导引过程。

三点法导引数学建模

数学模型推导

设制导站（跟踪雷达）坐标为 $S=[x_s,y_s,z_s]$，目标坐标为$T(t)$，导弹坐标为 $M(t)$。根据三点法导引规则，导弹位置始终满足：

$$M(t)=S+\lambda (t)\cdot \left(T(t)-S\right)$$

其中 $\lambda (t)\in [0,1$为比例系数，随时间递增趋近于1。

运动学方程

• 目标运动方程（假设匀速直线运动）：
  $$T(t+\Delta t)=T(t)+v_T\cdot \Delta t$$
• 导弹速度方向约束：
  导弹速度$v_M$方向始终沿$S-T(t)$连线方向，故导弹位置更新方程为：
  $$M(t+\Delta t)=M(t)+v_M\cdot \Delta t\cdot \frac{T(t)-S}{\Vert T(t)-S\Vert }$$

代码运行结果

界面示意图：

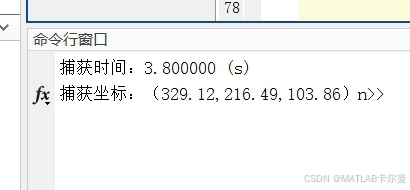
捕获时间与坐标（命令行窗口截图）：

代码结构：

MATLAB仿真代码

部分代码如下：

% 三点法导引，三维空间上的
% 2025-05-29/Ver1
clear; clc; close all;

%% 参数定义
% 制导站坐标（跟踪雷达）
S = [0, 0, 0];          % 假设雷达位于原点

% 初始目标位置与速度
T0 = [300, 200, 100];   % 目标初始坐标 (m)
vT = [10, 5, 0];        % 目标运动速度 (m/s)

% 导弹参数
vM = 100;               % 导弹速度 (m/s)
M0 = S + 0.1*(T0 - S);  % 导弹初始位置（靠近雷达）

% 仿真参数
dt = 0.1;               % 时间步长 (s)
totalTime = 20;         % 总仿真时间 (s)
steps = totalTime / dt; % 总步数

%% 初始化轨迹存储
% traj_T = zeros(steps, 3); % 目标轨迹
% traj_M = zeros(steps, 3); % 导弹轨迹
traj_T(1,:) = T0;
traj_M(1,:) = M0;

%% 三点法导引动态仿真

完整代码的下载链接：https://download.youkuaiyun.com/download/callmeup/90942866

如需帮助，或有导航、定位滤波相关的代码定制需求，请点击下方卡片联系作者