为什么需要轻量化网络

轻量化网络技术在无人驾驶、安防监控摄像头等应用中起着至关重要的作用，这些应用都需要算法在本地进行实时快速的推理，从而避免网络延迟导致的安全隐患。轻量化网络大大推动了边缘计算的发展，并且边缘计算的优势就在于保护数据隐私，在本地处理敏感数据，避免将信息上传至云端，减少了隐私泄露的风险。这就是轻量化网络的优势

自从AlexNet在ImageNet竞赛中获得冠军以来，CNN就开始飞速发展，像2014年牛津大学的VGGNet、谷歌的GoogLeNet，再到2015年微软研究院提出的ResNet，2019年谷歌的EfficientNet，甚至出现了ViT这种，一种全新的特征学习方法，这些方法在计算机视觉领域的准确率越来越高，但都是在网络变得更臃肿，参数量变得更多，计算量变得更大为代价的，这就加剧了学术界和工业界的分离，准确率越来越高的网络越来越臃肿，这使得内存量小、算力不足的边缘设备难以支撑先进算法的庞大身躯。

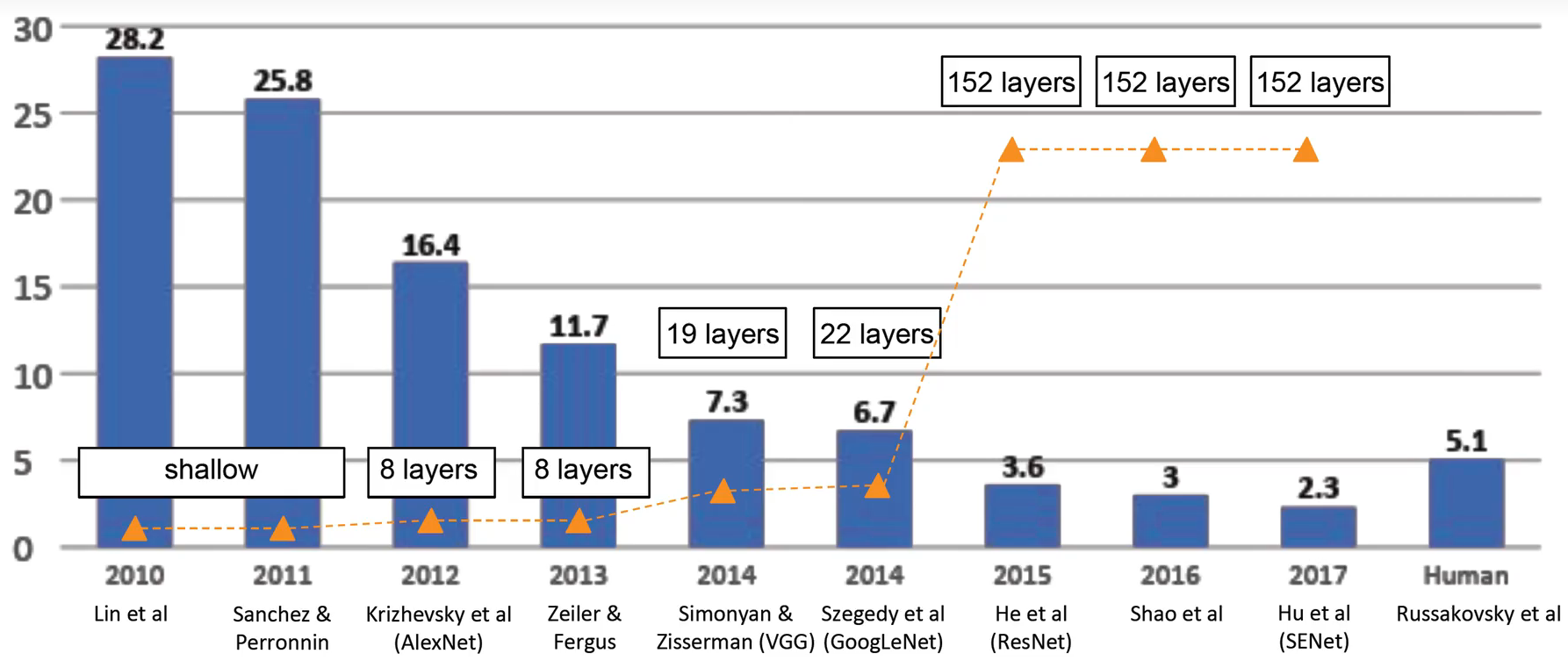
正因如此，我们不能再一味的去追求各大竞赛榜单上的排名了，我们应该开始兼顾网络的精度和速度，使得这个网络更加轻量化，可以部署在边缘终端设备上。

特别是我们身处一个万物互联的世界，有很多的智能穿戴和物联网的设备，都是部署再终端本地的，不一定要连接到因特网上，并且很多地方的信号是很差的，比如地铁或者偏远地区，像无人驾驶就是一种典型的实时边缘计算的场景，无人驾驶车上面配备了各种各样的传感器，像单目摄像头、双目摄像头、毫米波雷达、激光雷达、红外传感器等，都需要由汽车的本地计算机来进行推理，当场就要做出决策，否则要等到将数据上传到云端，再由云端处理完数据下达指令，汽车早就发生事故了。

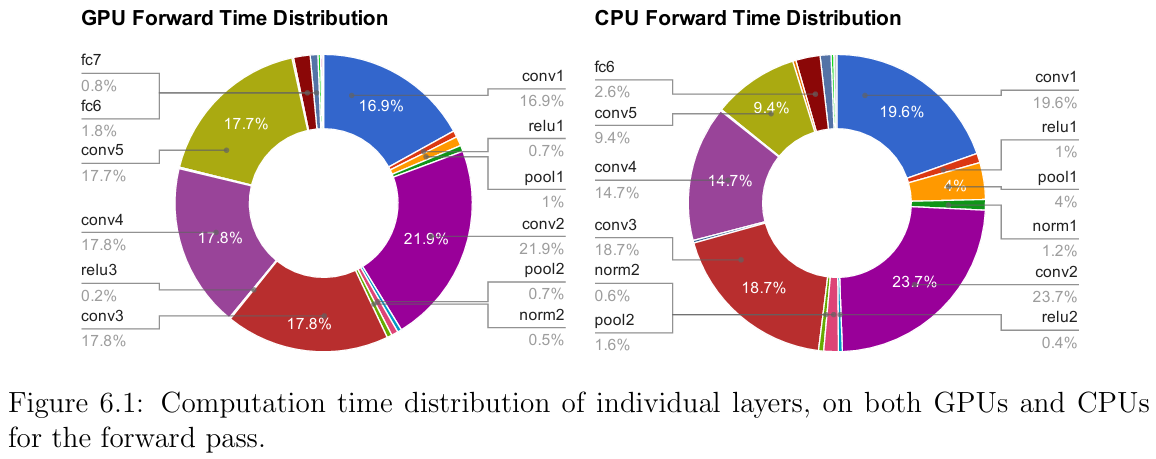
在贾杨清大神的博士论文中有两幅图，分别是在GPU上前向推理的耗时分布和在CPU上前向推理耗时的分布，其中卷积层是占了大部分的。从下图也可以看出，随着batch_size大小越大，卷积层运算所耗的时间就越长，站的比例越大。所以轻量化网络很大程度上是对卷积层进行优化（这里只涉及到CNN，之后会有注意力机制的优化），其实图中也可以看出在batch_size较小的适合，全连接层也很耗时，但现在很多网络都有各种各样的方法代替全连接层，所以也就解决了这个问题。

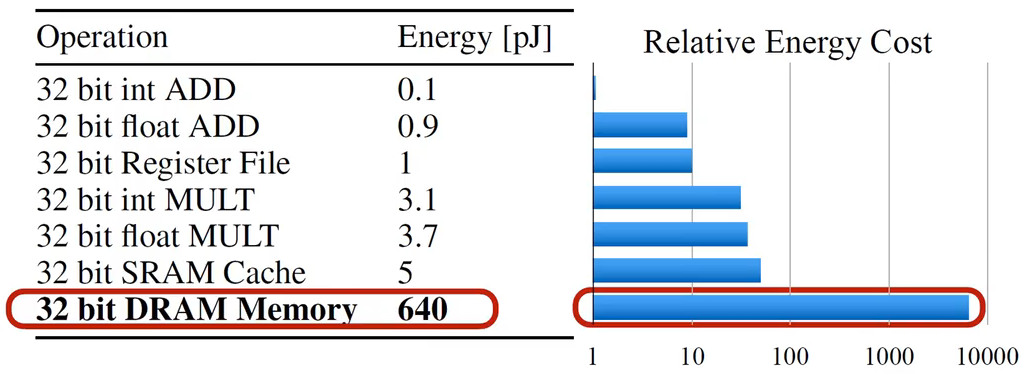
在韩松老师的课上，有这么一个表，32bit的整数加法，消耗0.1pJ，32bit的浮点数加法，消耗0.9pJ，32bit的寄存器文件处理消耗1pJ，32bit的整数和浮点数乘法分别消耗3.1和3.7pJ，最后32bit的SRAM的内存读取和DRAM的内存读取消耗的能量就更多了，而神经网络的训练和推理，就需要加载我们所设计好的神经网络，加载我们的网络权重，而轻量化网络很大程度上就是要较少内存的读写，从权重量本身就可以进行减少。

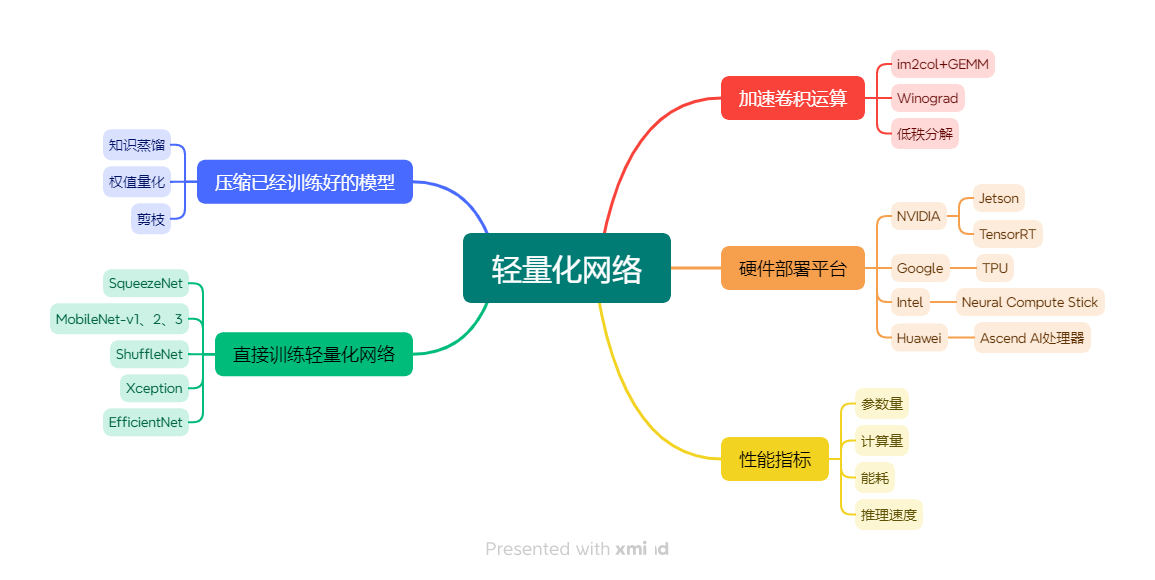
下图是进行移动端、终端边缘计算的方法，可以压缩已经训练好的模型，也可以直接训练轻量化的网络，可以加速卷积运算，硬件部署可以在NVIDIA的Jetson或者华为的Atlas200DK上部署。

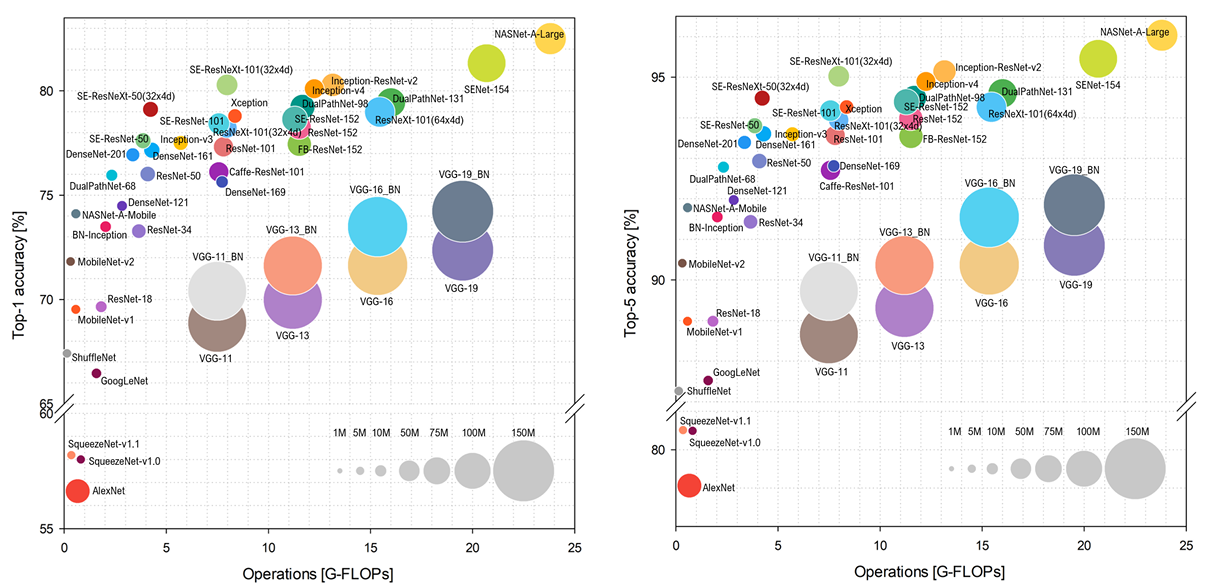
在这篇名为《Benchmark Analysis of Representative Deep Neural Network Architectures》的论文中，对不同深度神经网络架构的性能进行了基准测试和分析。其中有这么一张图，左图的竖坐标是Top1准确率，右图的竖坐标是Top5准确率，横轴是计算量大小，圈越大表示模型的参数量越大，我们当然希望模型参数量又小，计算量又小，准确率还高，也就是希望在图的左上角，可以看到有非常臃肿的VGG模型，也有比较轻量化的网络MobileNet、ShuffleNet。

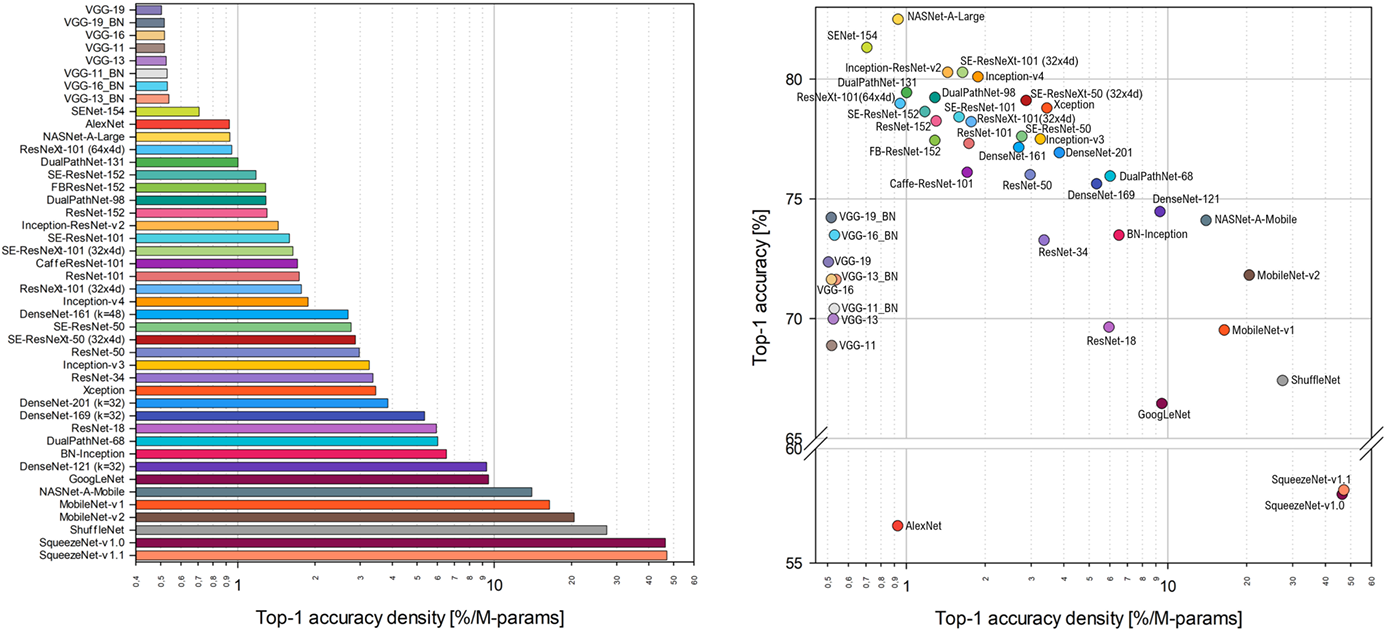
这两张图的左图表示的是，单位参数量对最终性能准确率的贡献，像VGG的参数效率就非常的低，而MobileNet、ShuffleNet这些轻量化网络的参数效率就相对较高，画成散点图就是右图。

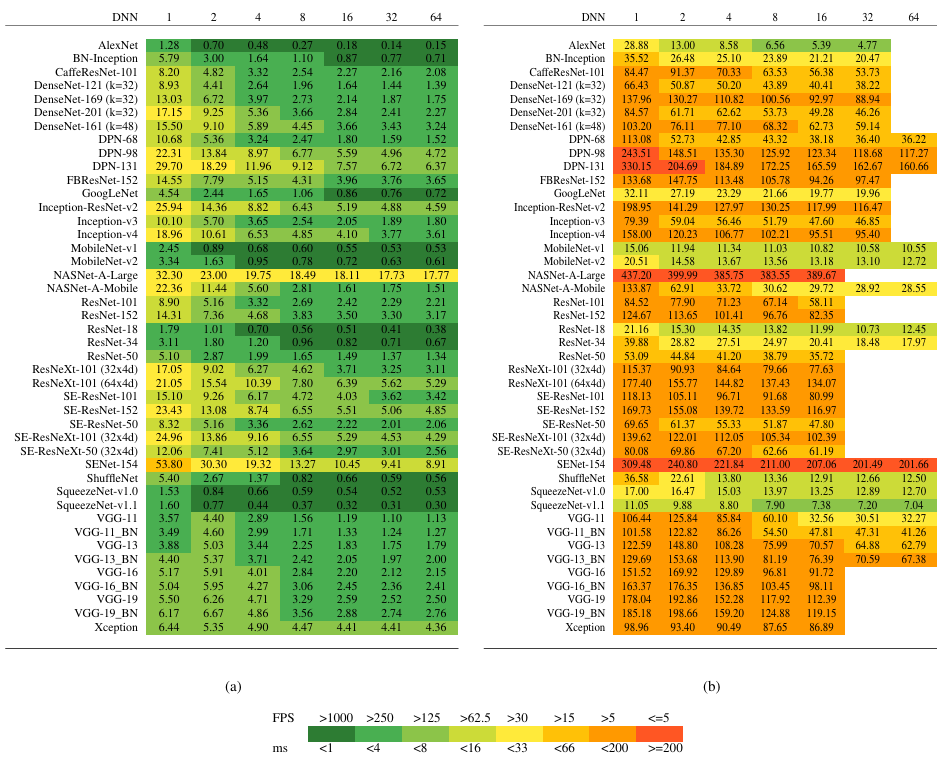
这张图展示了不同深度神经网络架构在两个硬件平台撒谎给你进行多个批次大小下的推理时间评估，同样也可以证明轻量化网络的优势。

注：以上内容为个人学习所用，通过对b站同济子豪兄的视频进行总结，若有侵权，联系删帖