1 非线性假设
前几章的学习中,我们对线性回归和逻辑回归有了一个大概的认知,但是在特征非常多的情况下,这两种方法都会存在严重的问题,那就是运算的负荷会变得非常大。
假设仅仅考虑二次项的情况,在极端情况下,设存在100个特征,最终会有5000个项,并且二次项增加的速率是 ,不仅如此,由于项数过多,甚至会出现过拟合问题,因此,我们需要一种新方法来解决这个问题,也就是人工神经网络。
2 人工神经网络
1 原理
人脑是现今为止人类所知的最神奇的学习机器,在解决复杂的机器学习问题时人类自然而然的会想到模拟人脑的原理创造出一种算法——人工神经网络,人工神经网络于二十世纪八九十年代兴起,但由于当时计算机性能有限,因此直到近年来才大规模兴起。下面我们将从生物学上的神经元开始,介绍人工神经网络的数学模型:
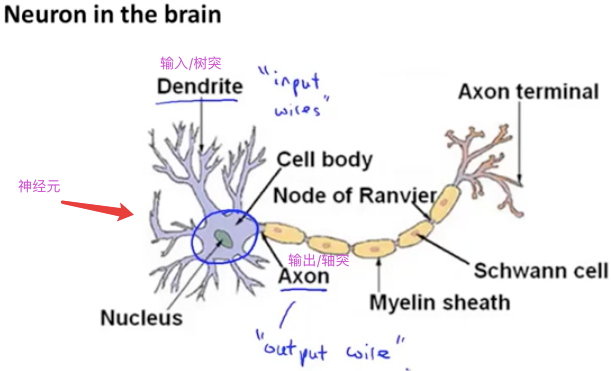
2 模型展示Ⅰ
上图是生物学上的神经元模型,我们使用逻辑单元来模拟神经元:
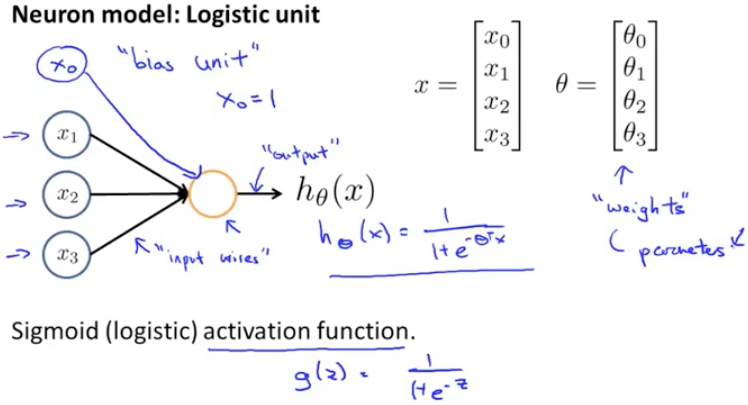
上图中 代表输入神经树突, 中间的黄色圆圈代表细胞核,最上面的
通常被称作偏置单元,一般置为1,而Sigmod函数一般被称作激活函数,相应的参数在神经网络中被称作权重。
下面我们将这些逻辑单元按不同层级组成神经网络,以下图为例:
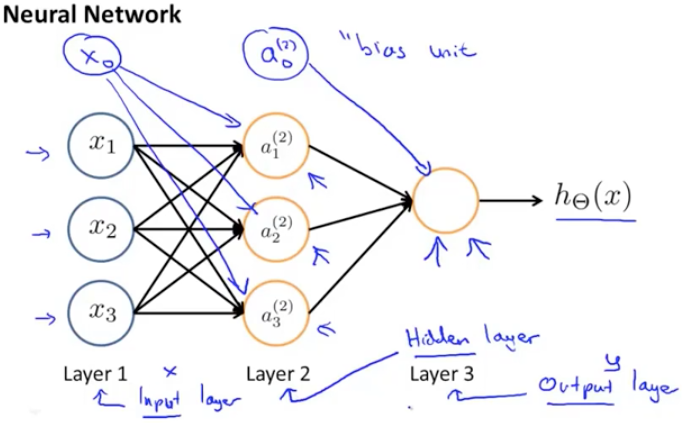
图中第一层是输入层,用来输入特征,第二层被称为隐藏层,之所以被称为隐藏层,是因为它的值在训练集中无法得知,既非x也非y,最后一层被称为输出层,输出假设的最终结果。最后,在每层都增加一个偏差单位。
为了方便描述,下面引入一些记号:
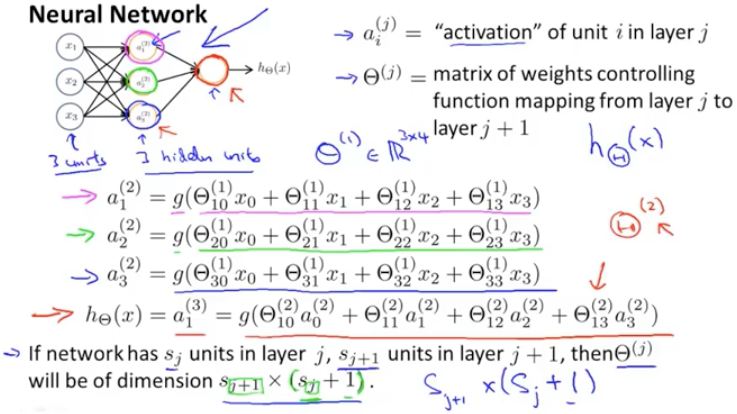
是第j层的第i个激活项,即一个具体神经元计算并输出的值,
是从J层映射到第J+1层的权重矩阵,其尺寸规定为行数为第J+1层的激活单元数量,列数为第J层的激活单元数量+1。在上图中进行的讨论只使用了一个训练实例,为了得到模型我们需要大量的训练样例。
3 模型展示 Ⅱ
我们可以通过使用向量和矩阵的表述使公式变得简单,令:
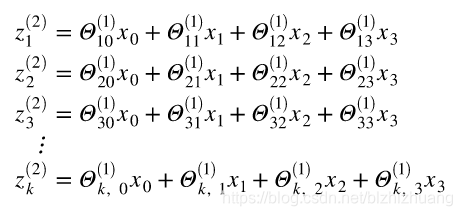
用向量表示可得:
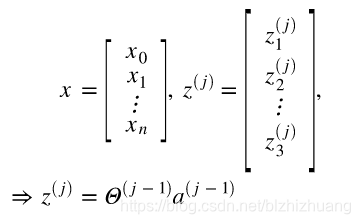
又因为通常情况下偏置项置为零,所以有:
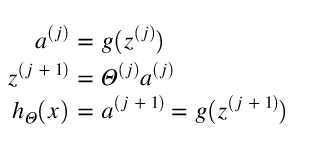
通过上面的表达式可以清晰的看出,神经网络与之前所学的逻辑回归最大的不同在于,它是将上一层的输出转化为下一层的输出,这种方法我们称之为前向传播。
如果我们把a0,a1,a2当作更高级的特征值,由于它们受梯度下降的限制,所以是变化的,可以在迭代中具有越来越优越的特性,更好的预测新数据。
3 特征与直观理解
利用神经网络进行逻辑与,非运算:
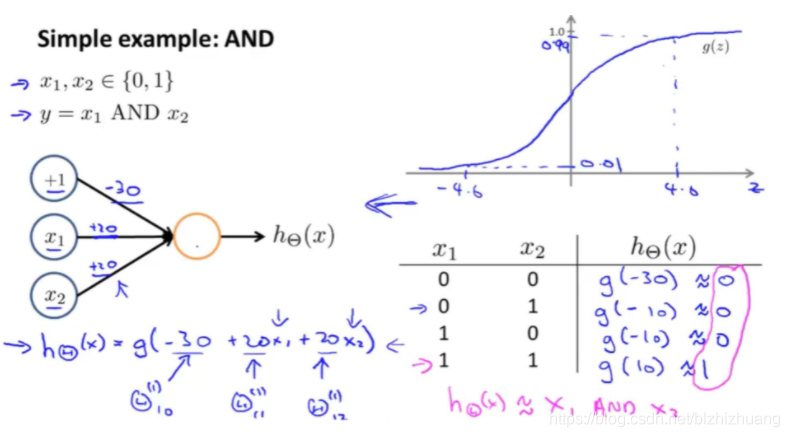
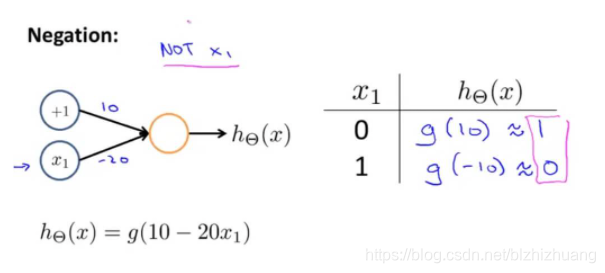
异或运算无法通过一层完成,这是由于输出函数本质上是一个线性函数,无法区分曲线所划分的训练集,为了解决这个问题,我们可以采用多层神经网络的解决方案。
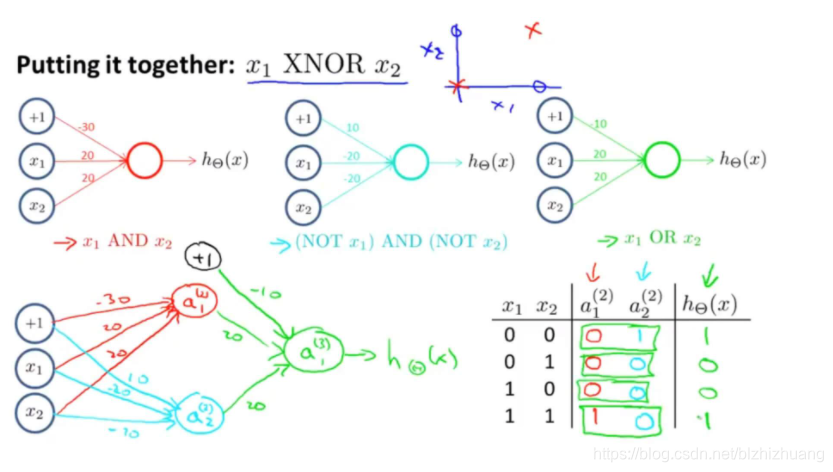
神经网络解决复杂函数的方式就和上述方法一样,通过增加层数来解决复杂运算的问题。
4 多元分类
对于分类问题有超过两个分类的情况,如何判别类别的,可以采用one-hot编码的思想,具体而言,比如对于有四个类别的问题,可以令输出层有四个神经元表示四类,也就是每层都会出现 ,且只有一个会为一,从而表示当前类。
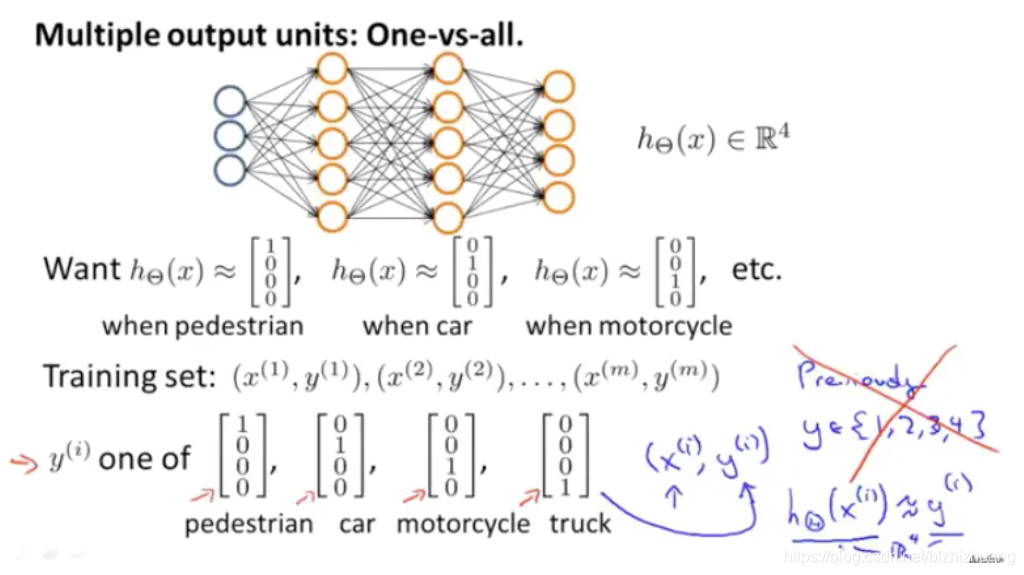
最后根据四个分类共同组成的结果判断类别。






















 1502
1502

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








