时序分析之静态分析基础SAT

最新推荐文章于 2023-12-31 00:27:48 发布

原创最新推荐文章于 2023-12-31 00:27:48 发布 · 2.2k 阅读

4 ·

CC 4.0 BY-SA版权

FPGA基础专栏收录该内容

4 篇文章

订阅专栏

本文深入探讨静态时序分析(SAT)的核心概念，包括时序模型、关键参数及其计算公式，如传播延迟(tpd)、时钟建立时间(Tsu)、保持时间(Th)、时钟到输出延迟(tco)等，旨在提升系统主频与稳定性。

静态时序分析（SAT）

静态时序分析的前提就是设计者先提出要求，然后时序分析工具才会根据特定的时序模型进行分析，给出正确是时序报告；

　　进行静态时序分析，主要目的就是为了提高系统工作主频以及增加系统的稳定性。对很多数字电路设计来说，提高工作频率非常重要，因为高工作频率意味着高处理能力。通过附加约束可以控制逻辑的综合、映射、布局和布线，以减小逻辑和布线延时，从而提高工作频率；

相关参数分析

tpd : propagation delay,定义由输入脚到输出脚最大延迟时间
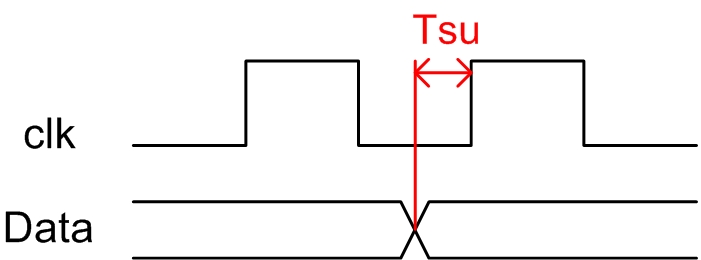
Clock Setup Time (Tsu)

建立时间（Tsu）：是指在时钟沿到来之前数据稳定不变的时间，如果建立的时间不满足要求那么数据将不能在这个时钟上升沿被稳定的打入触发器;

Clock Hold Time (Th)

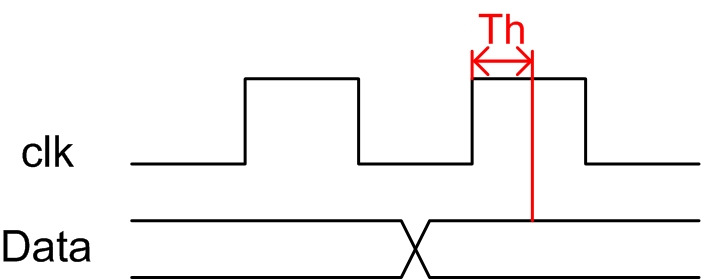
保持时间（Th）：是指时钟沿到来之后数据稳定保持不变的时间，如果保持时间不满足要求那么数据同样也不能被稳定的打入触发器;

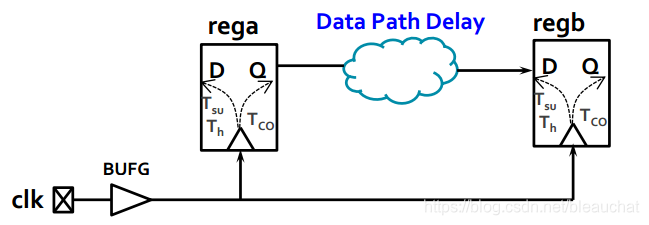
Clock-to-Output Delay（tco）

Tco是指时钟触发开始到有效数据输出的器件内部所有延时的总和。或简单地说,在时钟有效后，D的数据并不能立即传到Q端，这段等待的时间就是触发器的时钟到输出时间;

Clock skew

时钟偏斜（clock skew）：是指一个时钟源到达两个不同寄存器时钟端的时间偏移;

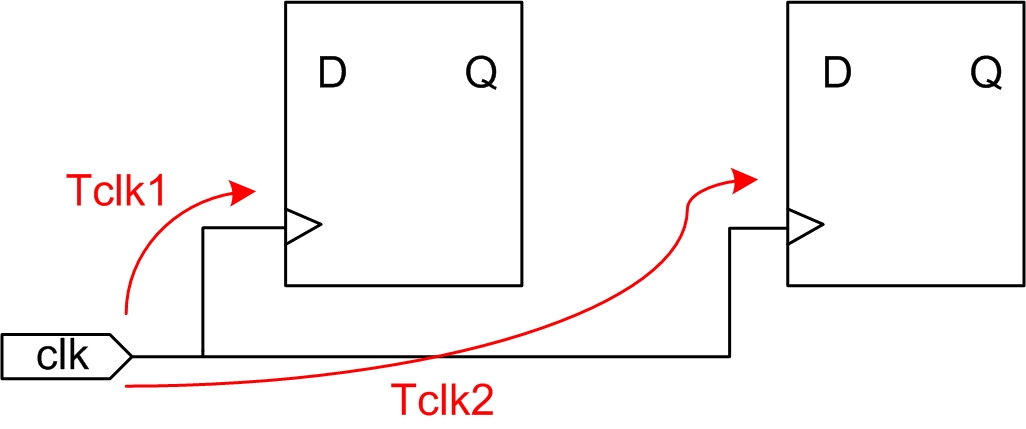
时钟偏斜计算公式如下：

Tskew = Tclk2 - Tclk1　

clock jitter

所谓抖动(jitter)，就是指两个时钟周期之间存在的差值，这个误差是在时钟发生器内部产生的，和晶振或者PLL内部电路有关，布线对其没有影响;简言之，skew通常是时钟相位上的不确定，而jitter是指时钟频率上的不确定（uncertainty);jitter 是由时钟源产生的抖动;skew是时钟树不平衡引起的到达两个寄存器的延迟差;

clock uncertainty = clock jitter + clock skew

Data Arrival Time

数据到达时间（Data Arrival Time）：输入数据在有效时钟沿后到达所需要的时间。主要分为三部分：时钟到达寄存器时间（Tclk1），寄存器输出延时（Tco）和数据传输延时（Tdata）;

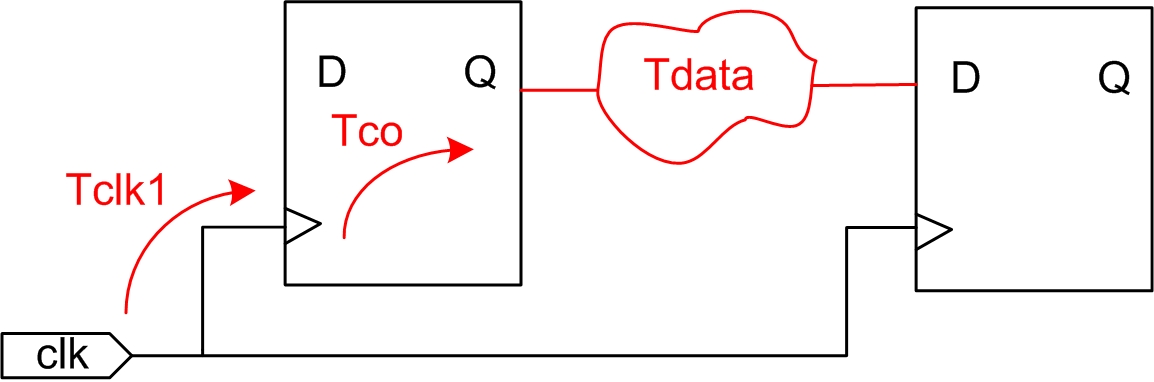
数据到达时间计算公式如下：

　　　Data Arrival Time = Launch edge + Tclk1 +Tco + Tdata　

Clock Arrival Time

时钟到达时间（Clock Arrival Time）：时钟从latch边沿到达锁存寄存器时钟输入端所消耗的时间为时钟到达时间

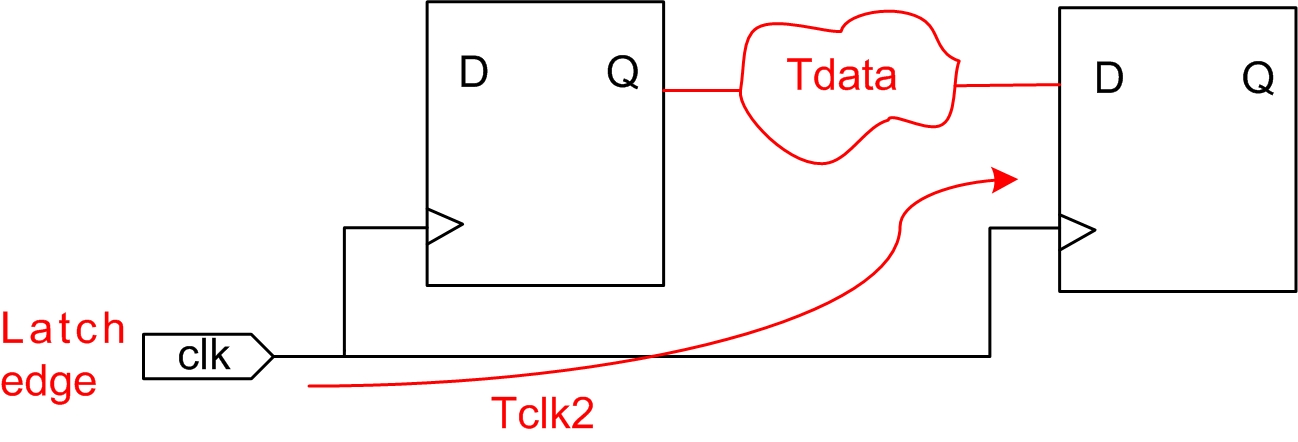
时钟到达时间计算公式如下：

　Clock Arrival Time = Lacth edge + Tclk2　

Data Required Time（setup/hold）

数据需求时间（Data Required Time）：在时钟锁存的建立时间和保持时间之间数据必须稳定，从源时钟起点达到这种稳定状态需要的时间即为数据需求时间;

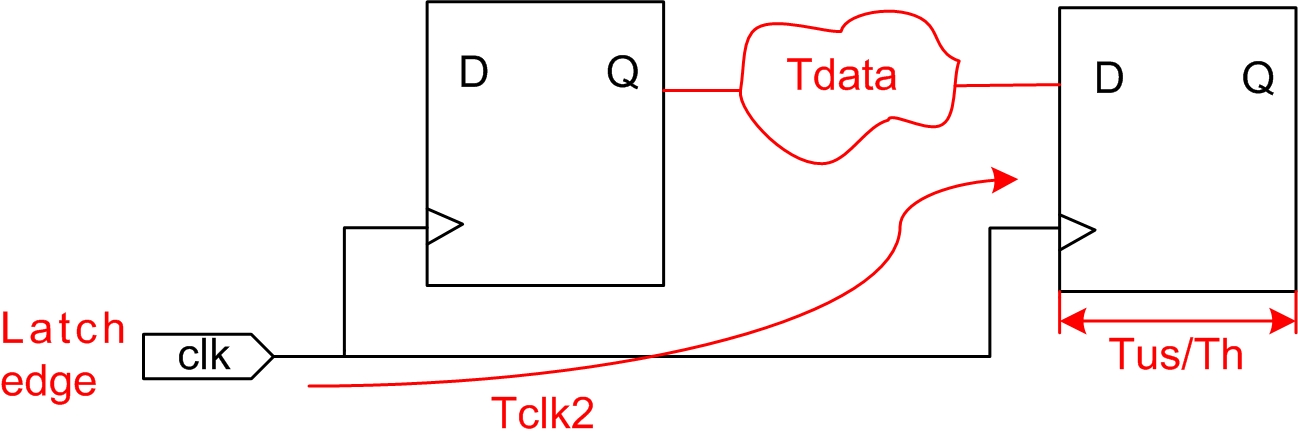
（建立）数据需求时间计算公式如下：

　　　　　　　　　Data Required Time = Clock Arrival Time - Tsu　　　　　　　　　　

（保持）数据需求时间计算公式如下：

　　　　　　　　　Data Required Time = Clock Arrival Time + Th　

Setup slack

建立时间余量（setup slack）：当数据需求时间大于数据到达时间时，就说时间有余量，Slack是表示设计是否满足时序的一个称谓;

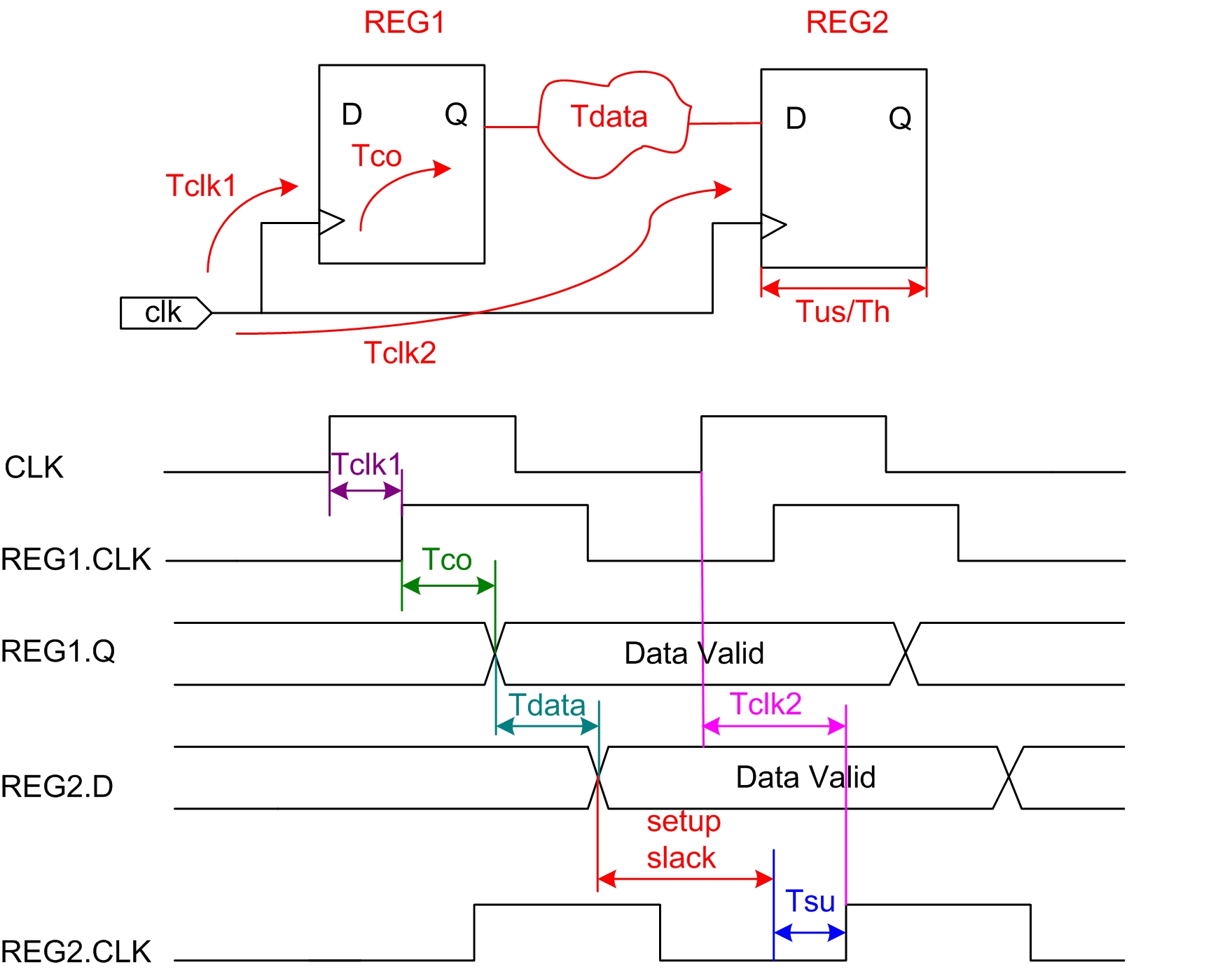
通过上面的介绍已经知道了建立（Setup）数据需求时间（Data Required Time）为：

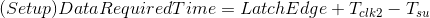
而数据到达时间（Data Arrival Time）为：

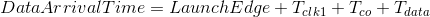
那么建立余量（Setup Slack）为：

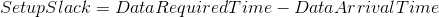
Setup Slack = Data Required Time - Data Arrival Time

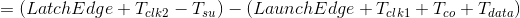
$= (Latch Edge +T_{clk2}-T_{su})-(Launch Edge+T_{clk1}+T_{co}+T_{data})$

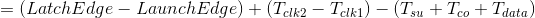
$=(LatchEdge - LaunchEdge)+(T_{clk2}-T_{clk1})-(T_{su}+T_{co}+T_{data})$

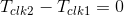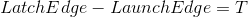这里假设时钟偏斜（Clock Skew）为0，也就是 $T_{clk2}-T_{clk1}=0$ ，同时 LatchEdge - LaunchEdge=T （这是很好理解的，这两个边沿之间的距离恰好是一个时钟周期）；

所以上式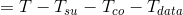 $=T - T_{su}-T_{co}-T_{data}$

建立时间裕量必须大于等于0，即T+Tskew>=Tco+Tsu+Tdata；其中Tdata=Tlogic+Trouting，假设Tskew=0，则T>=Tco+Tsu+Tdata，这个式子决定了系统工作的最大时钟频率！

这个最终结果说明了源寄存器与目的寄存器之间延迟 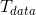$T_{data}$ 不能太长的原因，延迟越长，slack越小；

保持余量（Hold Slack）

同样，我们先看看数据到达时间以及保持（Hold）数据需求时间（Data Required Time）：

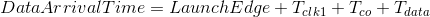
$Data Arrival Time = LaunchEdge +T_{clk1} + T_{co}+T_{data }$

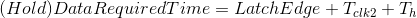
$(Hold)DataRequiredTime=LatchEdge+T_{clk2}+T_{h}$

如此以来，我们就可以得到保持余量（Hold Slack）为：

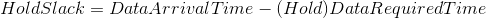
Hold Slack = Data Arrival Time - (Hold)Data Required Time

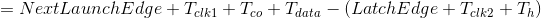
$=NextLaunchEdge + T_{clk1}+ T_{co}+T_{data}-(LatchEdge+T_{clk2}+T_{h})$

这里有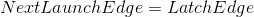： NextLaunchEdge= LatchEdge

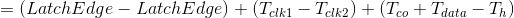
$=(LatchEdge - LatchEdge) + (T_{clk1}-T_{clk2})+(T_{co}+T_{data}-T_{h})$

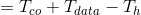
$=T_{co}+T_{data}-T_{h}$

从最终结果可以看出，这就是源寄存器与目的寄存器之间延迟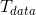 $T_{data}$ 不能太短的原因，时间太短，Hold Slack越小；

恢复和去除时间（Recovery and Removal Time）

对于一个异步复位寄存器来说，同样异步复位信号同样需要和时钟满足recovery time和removal time 才能有效进行复位操作和复位释放操作，防止输出亚稳态。

recovery time：恢复时间

撤销复位时，恢复到非复位状态的电平必须在时钟有效沿来临之前的一段时间到来并保持，才能保证时钟能有效恢复到非复位状态，此段时间为recovery time，类似于同步时钟的setup time，也就是说在时钟上升沿到来之前rst_n必须保持为1的时间；

如图所示，rst_n为0表示复位，clk上升沿触发，rst_n从0到1的上升沿与时钟上升沿必须不小于recovery time才能保证寄存器恢复到正常状态。

removal time ：去除时间

复位时，在时钟有效沿来临之后复位信号还需要保持为0的时间为去除时间removal time(去除时间)，类似同步时钟hold time；

如图所示，rst_n为0表示复位有效，clk为上升沿触发，rst_n保持为0经过clk上升沿后仍需要保持一段时间，才能保证寄存器有效复位，防止亚稳态

参考链接：https://blog.youkuaiyun.com/Reborn_Lee/article/details/81461955#%E6%95%B0%E6%8D%AE%E9%9C%80%E6%B1%82%E6%97%B6%E9%97%B4%EF%BC%88Data%20Required%20Time%EF%BC%89