0815个人学习日志

1.    在VGG论文中，Simonyan和Ziserman尝试了各种架构。发现深层且窄的卷积（即3×3）比 较浅层且宽的卷积更有效。
       （1）参数量显著减少：3×3 卷积核的参数量远低于同感受野大尺寸卷积核。例如，两个 3×3 卷积层（共 18 个参数）的感受野等效于一个 5×5 卷积层（25 个参数），但参数量减少约 28%。若替换为 7×7 卷积，三个 3×3 卷积层（27 个参数）的感受野与 7×7 卷积（49 个参数）相同，但参数量减少 45%。这种参数压缩不仅降低了过拟合风险，还减少了存储和计算开销。

       （2）计算效率提升：参数数量减少，带来了计算量的衰减。

       （3）非线性表达能力的增强：同感受野下，较小的卷积核意味着卷积层更多，可以插入更多的非线性映射函数。

       （4）增加了细节与层次优化：多个小卷积层的堆叠逐步扩大感受野，这种设计在保持全局语义信息的同时，通过逐层细化局部特征，避免了大卷积核对细节的模糊处理；随着层数的叠加使网络能从低级边缘特征逐步过渡到高级语义特征。

       （！）1×1 卷积虽能增加线性变换，但缺乏空间上下文建模能力，导致性能逊于全 3×3 架构。

2.    在numpy创建的数据默认类型为float 64，而在pytorch创建的数据默认类型为float 32。如果在需要把numpy数据转换成torch类型时，需要手动对齐数据类型，避免因为数据类型不同而不可计算。

3.    加性注意力（Additive Attention）其分数通过类似单层感知机的结构计算，将查询和键映射到同一空间后相加，再经非线性激活和线性变换。                                    

其分数的计算引入了非线性压缩（tanh） 和参数化映射，天然限制了分数的极端值，使得分数分布更平缓，最终权重更均匀。

而点积注意力（Dot-Product Attention）其分数直接通过查询（q）和键（k）的点积计算（其中 dk​ 是键 / 查询的维度，缩放是为了缓解高维时的数值膨胀）。  

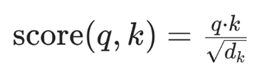
点积的本质是 “向量相似度的直接度量”，其分数的数值范围受输入维度和元素分布影响较大；这种 “两极分化” 的分数分布，经过 softmax 后会被进一步放大。从而呈现出高度注意力效果。

点积注意力因计算效率更高（可通过矩阵乘法并行实现）被广泛用于 Transformer 等模型；而加性注意力的均匀性在某些场景（如需要关注多个相关元素时）可能更有优势，但计算成本更高。