

利用偏导数计算方向导数


其中梯度定义:
gradf =

梯度是向量。
方向导数=梯度*单位向量
方向导数是数值, 梯度和单位向量相乘,是向量点积(参见前面的图)。
- 方向导数 = cos(θ) × 梯度,因此,所有的下降方向中,梯度方向下降最多。θ为方向导数所取方向与梯度的夹角。
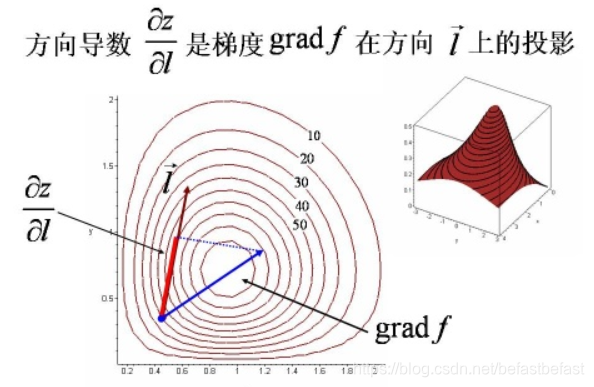
举例说明:z=f(x,y) 在(x0,y0)处的梯度为(3,4),即
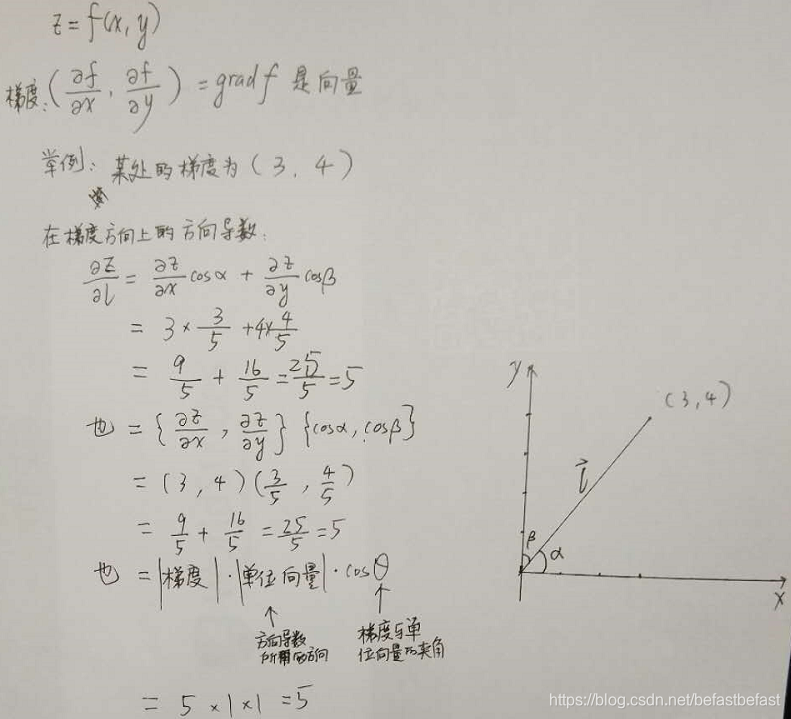

参考 http://xuxzmail.blog.163.com/blog/static/251319162010328103227654/
 本文介绍了如何利用偏导数计算方向导数,并详细解释了梯度的含义。梯度是一个向量,方向导数等于梯度与单位向量的点积,表示在特定方向上的最快变化率。在所有下降方向中,沿着梯度方向的变化最为显著。
本文介绍了如何利用偏导数计算方向导数,并详细解释了梯度的含义。梯度是一个向量,方向导数等于梯度与单位向量的点积,表示在特定方向上的最快变化率。在所有下降方向中,沿着梯度方向的变化最为显著。


利用偏导数计算方向导数


其中梯度定义:
gradf =

梯度是向量。
方向导数=梯度*单位向量
方向导数是数值, 梯度和单位向量相乘,是向量点积(参见前面的图)。

举例说明:z=f(x,y) 在(x0,y0)处的梯度为(3,4),即
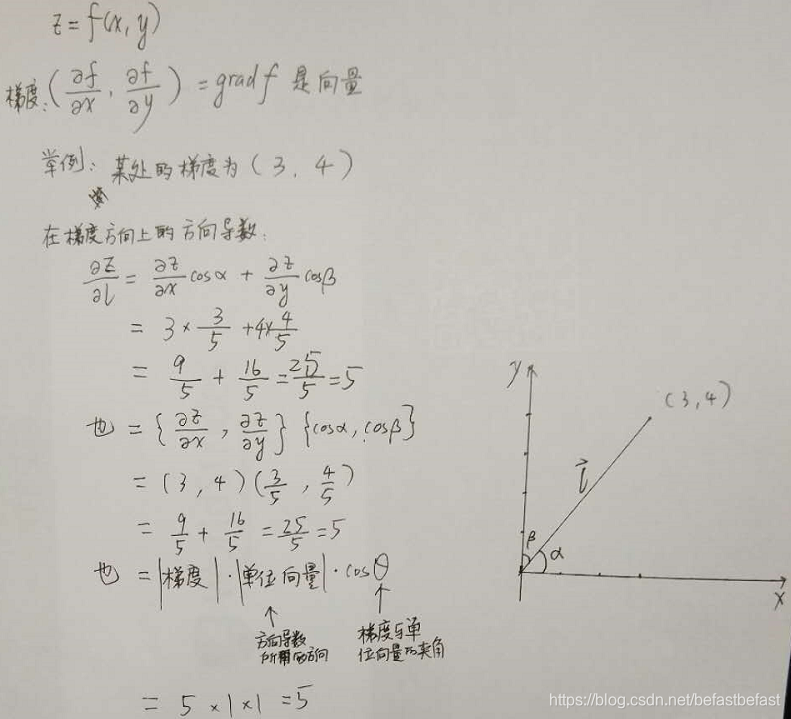

参考 http://xuxzmail.blog.163.com/blog/static/251319162010328103227654/
 1万+
1万+
 1176
1176

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


