一、矩阵相乘
1、概述
矩阵相乘的标准方法不是将一个矩阵的每个元素与另一个矩阵的每个元素相乘(称为元素乘积),而是计算行和列之间的乘积之和,也叫矩阵乘积,计算如下:
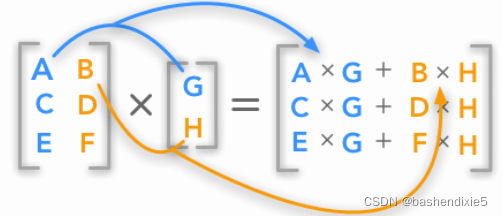
第一个矩阵的列数必须等于第二个矩阵的行数。如果第一个矩阵的维度是(m×n),则需要第二个矩阵的维度必须为(n×x),得到的结果矩阵的维度为(m×x)。
2、示例1
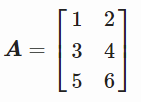
 本文详细介绍了矩阵乘法的概念、示例及现实意义,强调了矩阵相乘的条件和计算方法,并通过生活实例解释了矩阵乘法的应用。同时,文章探讨了点积的性质,包括不可交换性,并通过代码示例加深理解。最后,文章引入了线性方程组,阐述了如何用矩阵描述线性方程组及其解决方案。
本文详细介绍了矩阵乘法的概念、示例及现实意义,强调了矩阵相乘的条件和计算方法,并通过生活实例解释了矩阵乘法的应用。同时,文章探讨了点积的性质,包括不可交换性,并通过代码示例加深理解。最后,文章引入了线性方程组,阐述了如何用矩阵描述线性方程组及其解决方案。
矩阵相乘的标准方法不是将一个矩阵的每个元素与另一个矩阵的每个元素相乘(称为元素乘积),而是计算行和列之间的乘积之和,也叫矩阵乘积,计算如下:

第一个矩阵的列数必须等于第二个矩阵的行数。如果第一个矩阵的维度是(m×n),则需要第二个矩阵的维度必须为(n×x),得到的结果矩阵的维度为(m×x)。
 8528
8528
 3万+
3万+