代数 基础1

宝东老师的有两套视频
https://www.bilibili.com/video/av24188459
https://www.icourse163.org/course/HIT-1002117005

---

1、 全排列

（1）排列：像 1、2、3、4 … n 这样一堆有顺序的数 $\color{red}{\bigstar}$ ，放在一起
（2）用 $\mathcal P_1, P_2 \ldots P_n$ 代表第1，第2 … 第n个数。则存在的排列共有$n!$种 ( $\prod_{i=0}^n n$ )

2、逆序数

在排列中取任意两个数，组成 $\mathcal (P_i, P_j)$ 序对，如果 $\mathcal P_i > P_j$ , 则当 1, 否则当0.

$\color{purple}{\tau ( 3 1 2) = 0 + 1 + 1 = 2 }$

3、奇偶排列

（1）偶排列

逆序数是偶数

自然排列（ 1，2，… , n ）逆序数是0，也属于偶排列

（2）奇排列

逆序数是奇数

---

定理：对换改变奇偶性

证明：分两种情况
1、相邻对换时，设

$$\begin{align*} a_1 a_2 a_3 ··· a_s \ a \ b \ b_1 b_2 ··· b_t \; \tag{1} \\ a_1 a_2 a_3 ··· a_s \ \color{blue}{b \ a }\ b_1 b_2 ··· b_t \; \tag{2} \end{align*}$$

( $1^o$) a < b 时。 $$\underbrace{ a_1 \cdot a_i \cdots a_s }_{s} \qquad \underbrace{ b_1 \cdot b_j \cdots b_t }_{t}$$

在(1)、(2) 的 $a_1 \sim a_s ，b_1 \sim b_t$ 中任意的 $a_i , b_j$ ，它的逆序数是相同的。所以只考虑 $a \ b$ 位置

又此时 $\tau ( b, a ) = 1$ 。所以 $a$ 在（1）中的逆序数比（2）中大1。

$b$ 在 (1)(2) 中逆序数相等。（ (1) 前面插的 $a$ 比 $b$ 小)
总的来看，全排列（2）的逆序数比（1）大1。所以(1),(2) 奇偶性相反。

( $2^o$) a > b 时

同理，此时(1)中 $\tau ( a, b ) = 1$ ，逆序数比 (2) 大1，两者奇偶性相反。

2、一般对换时，设

$$\begin{align*} a_1 a_2 a_3 ··· a_s \ \color{purple}{ a }\ b_1 b_2 ··· b_t \ \color{purple}{ b } \ c \ c_1 c_2 ··· c_m \tag{3} \\ a_1 a_2 a_3 ··· a_s \ \color{blue}{ b }\ b_1 b_2 ··· b_t \ \color{blue}{ a } \ c \ c_1 c_2 ··· c_m \tag{4} \end{align*}$$

( $1^o$) 将（3）中的 $b$ 依次往左和 $b_1 b_2 \cdots b_t$ 作相邻变换，得到 $$\begin{align*} a_1 a_2 a_3 ··· a_s \ \color{blue}{ a \ b } \ b_1 b_2 ··· b_t \ c \ c_1 c_2 ··· c_m \tag{--} \end{align*}$$

一共经过 t 次变换。

( $2^o$) 再讲 $a$ 往后与 $b \ b_1 b_2 \cdots b_t$ 作相邻变换，到原来 $b$ 位置，得到（4）

一共经过 t+1 次对换。

( $3^o$) 总的，一共得到 $2t+1$ 次对换。

也就是增加了新排列的逆序数 = $\tau (原排列) + 2t + 1$ ，原来是偶现在肯定编程奇，原来是奇现在肯定变成偶。即（3）和（4）奇偶性肯定相反。

证毕。

$\bigstar$ 利用定理可以推出：
排列n >=2时，里面奇偶排列的个数各占一半。

---

4、行列式的定义

相关阅读 https://www.zybuluo.com/yangfch3/note/271783

二三阶

主对角线取正、次对角线取负

$\left | \begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix} \right | = a_{11} a_{22} - a_{12} a_{21}$

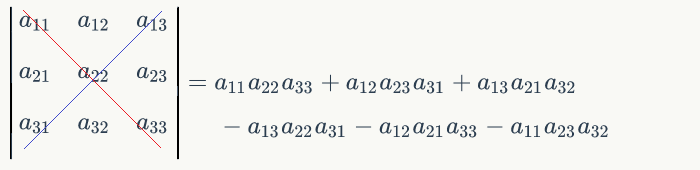分析

(1) 几阶就有 $n!$ 个项 （3阶就是6个）

(2) 所有可能的取自不同行不同列的 3 个元素之积

行指标按自然顺序排列时，列指标(123)(231)(312)为正，(321)(213)(132)为负<
通项： $(-1)^{\tau ( \mathcal{ P_1P_2P_3 )}}{ a_{1P_1}a_{2P_2}a_{3P_3}}$

N 阶行列式
取自不同行不同列的N个元素之积

$$\left| \begin{matrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{matrix} \right| = \sum_{P_1P_2···P_n}\mathcal{ (-1)^{\tau ( P_1P_2P_3 )} a_{1P_1}a_{2P_2}a_{nP_3}}$$

直接用通项取解问题几乎是不可能的。但是可以用来解决特殊的行列式。比如上三角行列式。

$$\left| \begin{matrix} a_{11} & a_{12} & \cdots & a_{1n} \\ 0 & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ 0 &0 & \cdots & a_{nn} \\ \end{matrix} \right| = (-1)^{\tau (12···n)}a_{11}a_{22}···a_{nn} = a_{11}a_{22}···a_{nn}$$
同样的，下三角行列式也是这个结果。

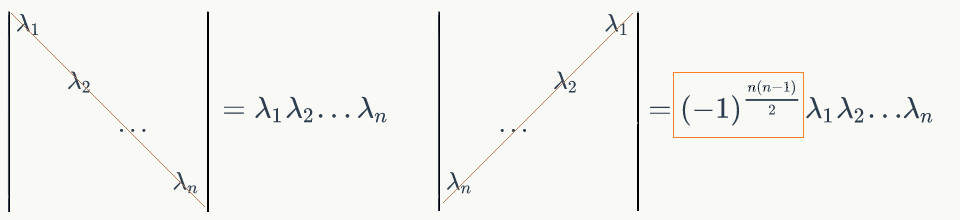
自然而然的，就会想有没有办法把一般行列式转换为这类特殊行列式？引出行列式的性质

(本节完)

---