太极图形0，1

序

图形学，了解的不多。

只知道，写一点shader，可以渲染出图形。

但是，这个学，它所见即所得，比较直观，当然，对我这样的普通的人，很难，因为要用数学，而且我还不怎么会编程。

两点论，这个就是两点，优点，缺点。

大概是按着这个系列的视频来的太极图形的个人空间_哔哩哔哩_bilibilihttps://space.bilibili.com/1779922645/channel/seriesdetail?sid=337716

下面这个是一点相关的链接： 

•  GitHub上的课件：

taichiCourse01 (TaichiCourse) · GitHub

能把这个GitHub导入到gitee里吗？

• 在线taichi：

在线的话，浏览器web端，只支持CPU，可能会慢点。

Taichi Zoo Tutorial

• 文档

当然，我这样的小白，是看不懂文档的……里面有个示例代码。

Getting Started | Taichi Docs (taichi-lang.org)

下面的主要是视频合集里的第一个，看的时候记的一点东西。

太极图形课S1第00、01讲：课程概览，什么是图形学和taichi？taichi的数据、计算核与可视化_哔哩哔哩_bilibili

安装

 pip install taichi

我也只会这个了。

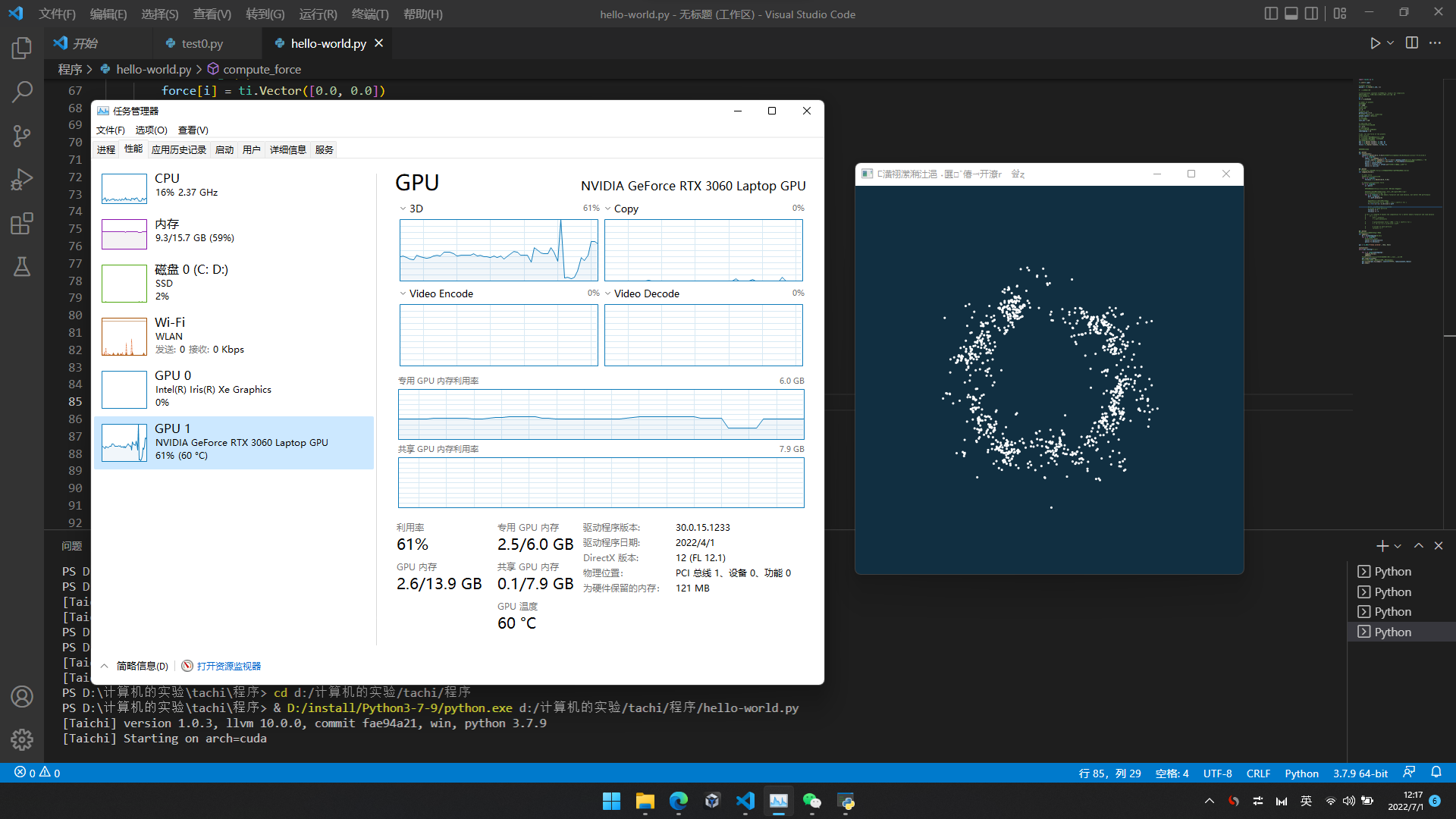
安好了吗？找点例子来试一试。就用上面文档里的吧。C,V,运行。

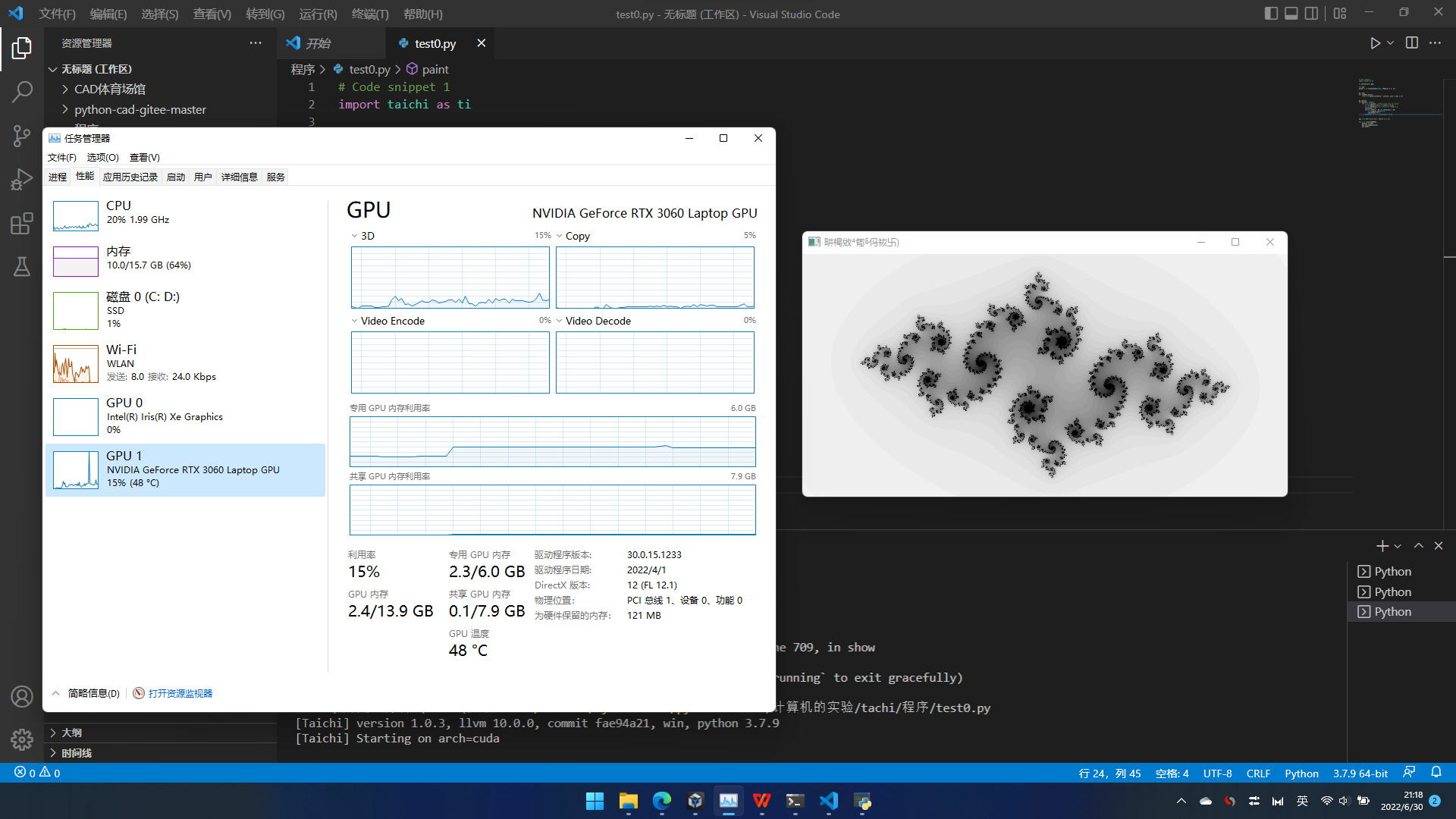
 笔记本，3060，在我这样不会编程的人手里，就是暴殄天物呐……

它的学名，叫Julia Set

好像改点参数，就会大变样，具体的不会。看看热闹算了……

初始化一个Taichi程序

从这个开始，主要内容是hello world的程序。

程序在这里：

Taichi Zoo Playground

运行出来长这样：

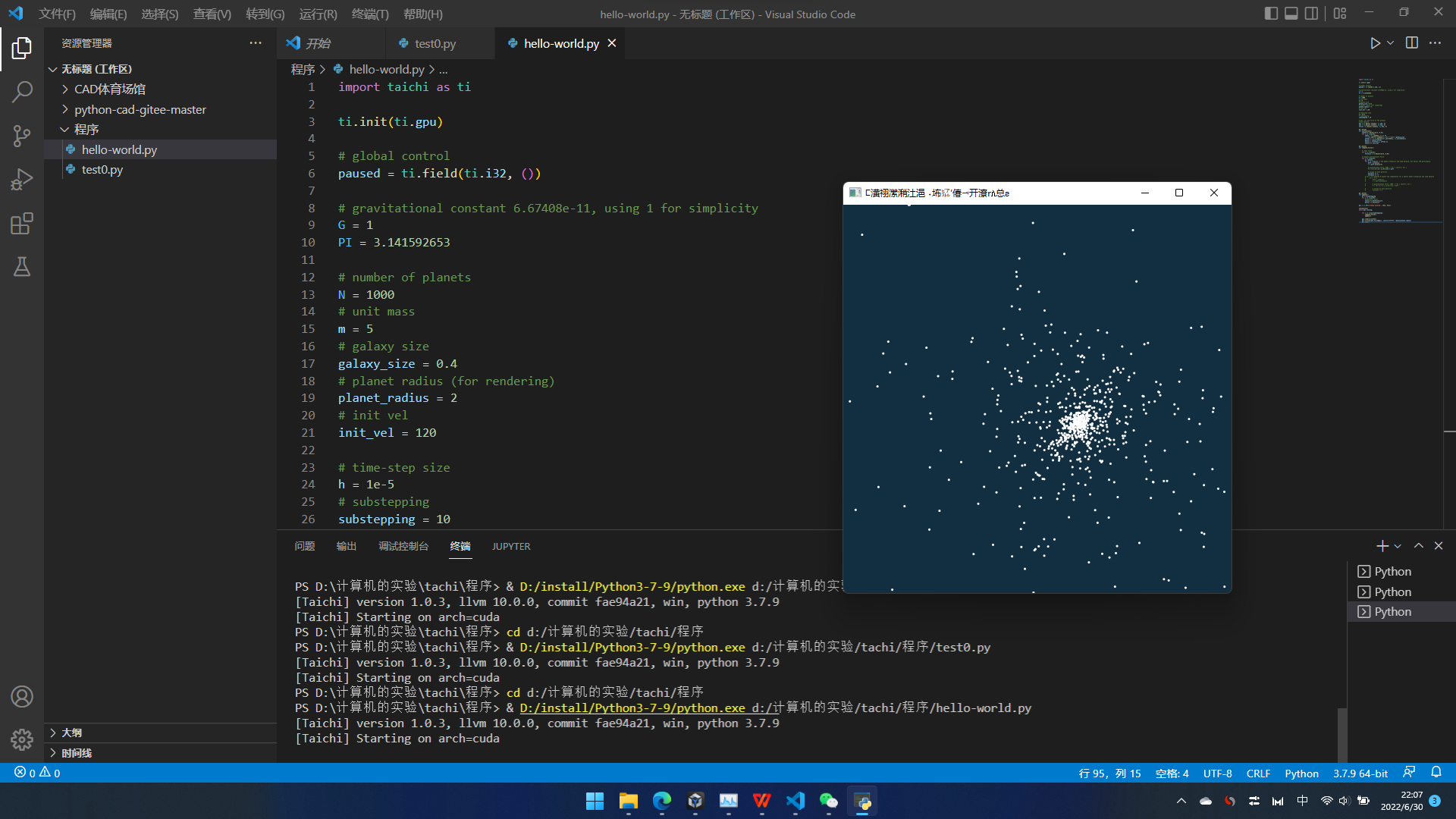
 初始化，主要靠这两行。 那个init，是程序入口。

scope：范围。

不是所有的代码都是taichi代码，在范围内的才是。

 再具体点，在这俩范围内的才是。

 组织Taichi的数据

数据。。图形什么的。

图形就是数据计算出来的嘛。

标量

隐式转换

 显示转换

 矢量

向量，矩阵，一个记录了起点，方向，长度的表示RT里一条光线的结构体什么的，都是矢量。

 为了简化矢量的定义，还提供了相关的关键字

这些矢量，可以用索引访问，就像python

这个，别的没有。可以表示256*256的热力图

field：域，场

 猜一下，这个是干嘛的？

OpenGL的帧缓冲区？存像素的？有可能。

怪不得这个变量其他编程语言没有……

全局的，灵活的。

 也可以通过索引访问

标量场？NONE?

一点例子

 上面那个你好世界，学名叫N体系统，就用到了这些变量，数据。

左边是python的，右边是taichi的数据。

 了解Tahichi的计算核

大概是这俩

这俩的存在有啥意义？

ti.kernel修饰的，会被并行执行，快。

 并行处理……双重for循环……CAD直线的连接？

Taichi里最外层的for循环，可以被并行化，也只有这个情况才能并行化。

 所以，为了按需并行，有时得改变一下写法

 并行了以后，快了。但是，世上事情难两全。比如，并行了break就不能用了，因为相互之间独立了。

 并行，+=会自动加锁。第3个的话，不会自动加锁，可能并行出问题。

 特有的for迭代，只在最外层支持。

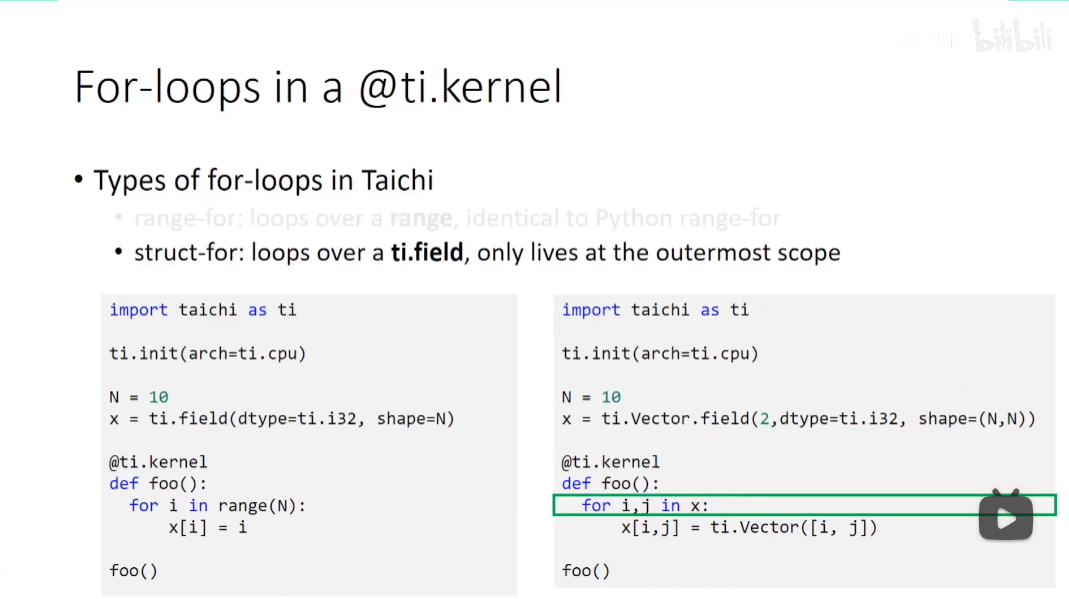
 从python向taichi传参的时候，需要写类型。

目前只能传标量，传矢量得手动搞一搞。

 都是值传递

返回值，会返回233

下面的是，那俩的另一个。它只能被ti.kernel调用。

 好像是在taichi里起复用的作用的。

可以嵌套，但是不能递归，因为强制内联了

拷贝了一次，值传递的内联，不是那种宏的单纯替换的内联

 一定要带出来，可以return

都是静态的

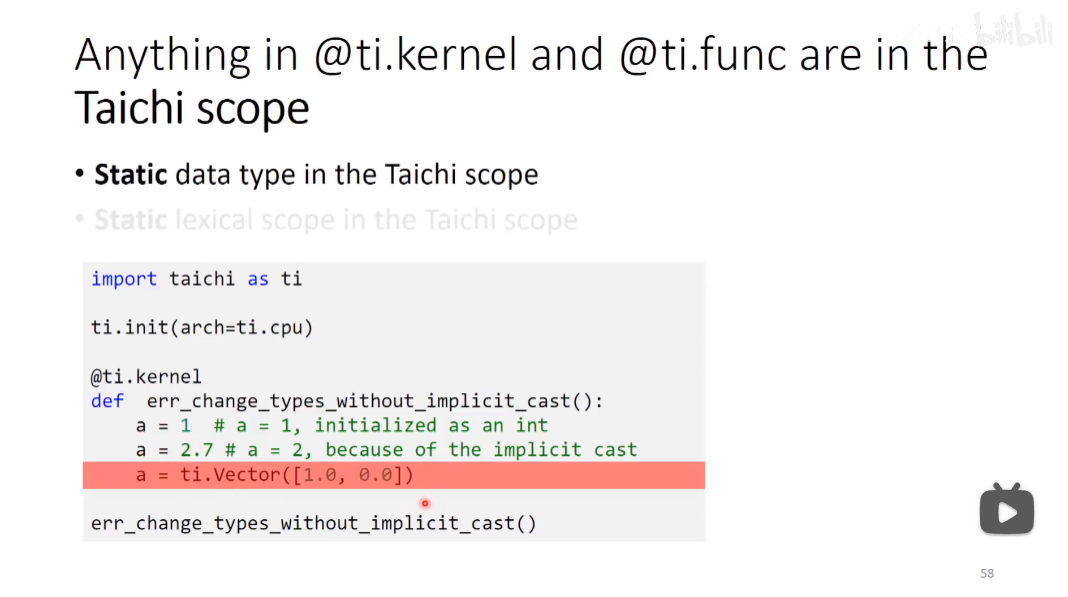
释放掉以后，再打印就报错

 只有field，才是全局的。

为什么这么设计？——大概是因为Python是弱类型，两次调用同一个函数的时候全局变量可能已经是不同的类型了。所以Taichi才做了这样的设计。

有的弹幕说的——感觉一切的设计，都是为了并行化，有道理呐…… 

 若干数学运算

回到你好世界，看一看这些并行化的for

 可视化Taichi程序

print

print，其实也算可视化……

 这个print，和python的稍微有点不同。比如，并行print会不按顺序来，是随机的。

 也不一定会按前——中——后的顺序来

 GUI

G_U_I，龟。

很多函数

 目前，比较慢，只有2D

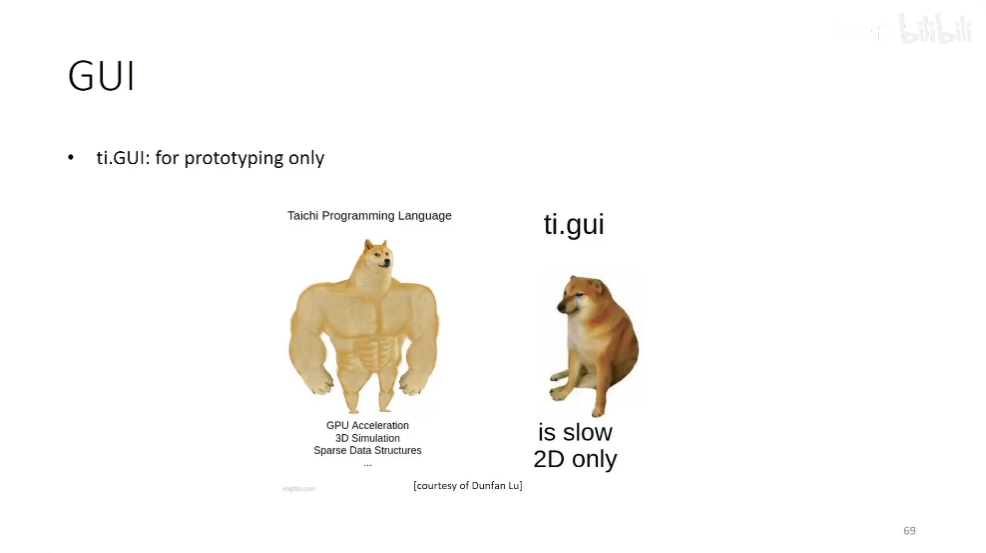
 想3D的话，可以导出为PLY，送到hodini里去渲染。

讲完了这些，就可以去你好世界了。

程序设计方面，就没啥问题了。

大概是这个流程。

 

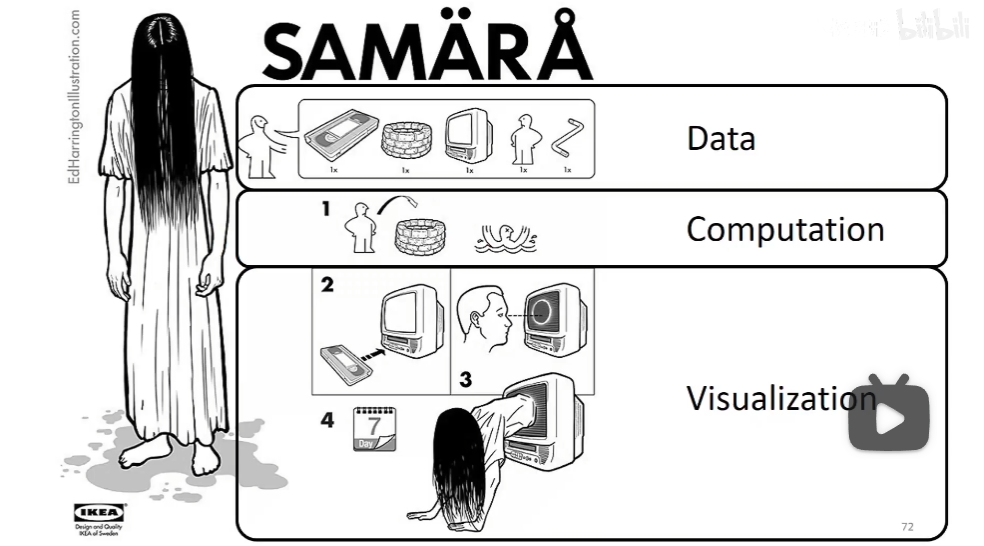
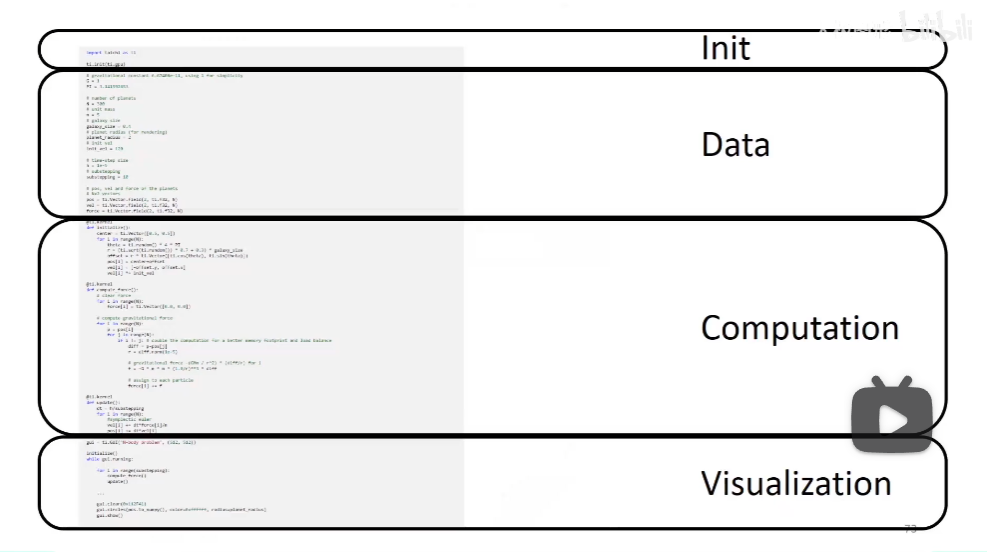
 doc是最好的老师……

但是，我这样的，看不懂啊……

现在的话，可以把julia-set分形这玩意搞明白，改一改。

 对物理仿真感兴趣的话，可以搞一搞这个多体问题

 没了。结束。

你好-世界

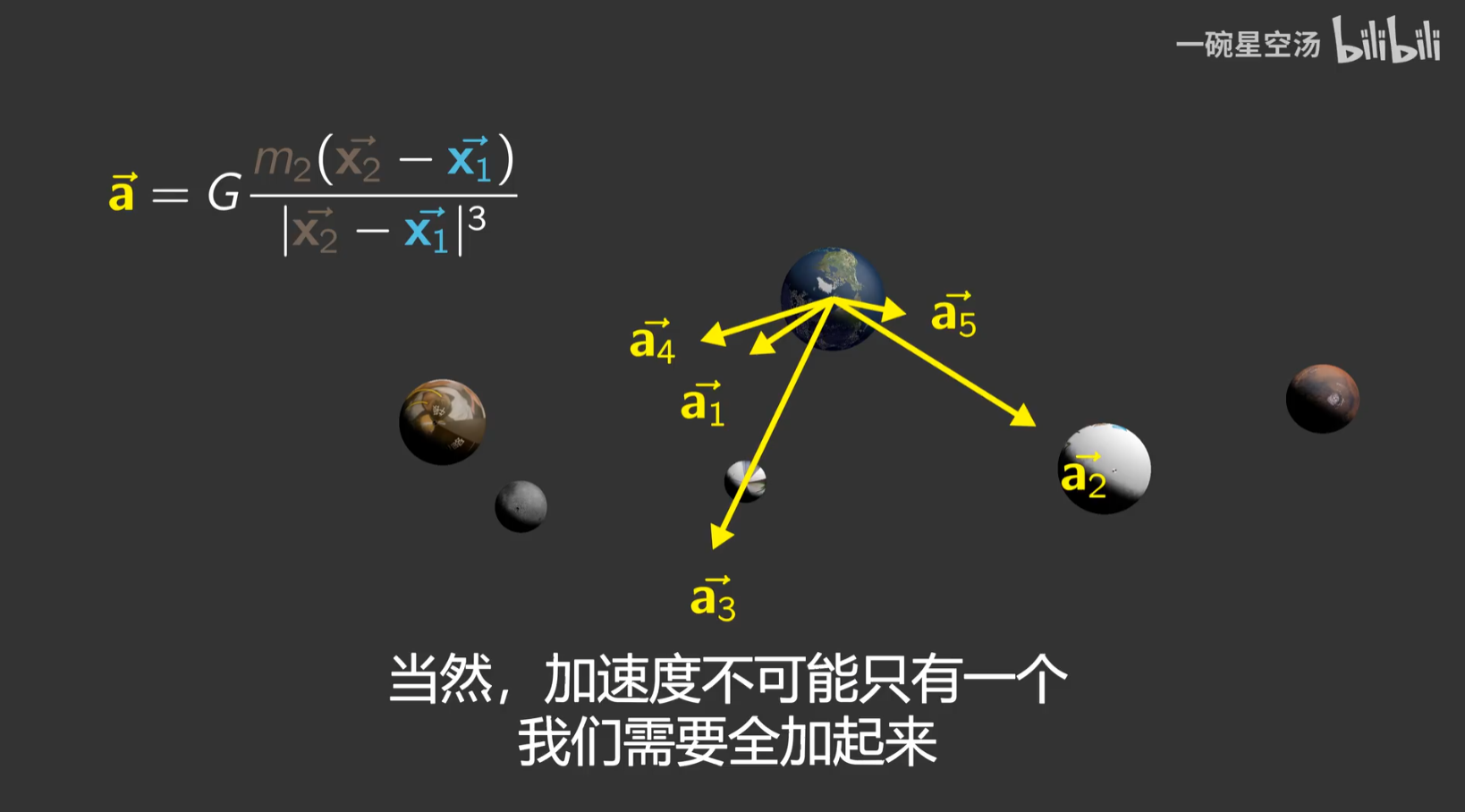
N体问题的解释。

数学原理

手把手教你模拟n体运动_哔哩哔哩_bilibili

上面那个视频里介绍了其中的数学原理，简单的说，就是这个：

相互作用，共同运动。

 具体实现（Taichi）

import taichi as ti

ti.init(ti.gpu)

# global control
paused = ti.field(ti.i32, ())

#一些常数的设置

# gravitational constant 6.67408e-11, using 1 for simplicity
#引力常数，是一个很小的值，这里设置为1，为了简化
#G=6.67408e-11
G = 1
PI = 3.141592653

# number of planets
#天体数量
N = 1000
# unit mass
#天体质量
m = 5
# galaxy size
galaxy_size = 0.4
# planet radius (for rendering)
planet_radius = 2#2pixel
# init vel
#初始化速度
init_vel = 120

# time-step size
#仿真时间间隔，10微秒
h = 1e-5
# substepping
#把每个10微秒再分成10步
substepping = 10

# pos, vel and force of the planets
# Nx2 vectors
#每个天体的位置、速度、力；场，域
#一个天体的位置，需要一个2维向量
#N个就需要N个，很合理
pos = ti.Vector.field(2, ti.f32, N)
vel = ti.Vector.field(2, ti.f32, N)
force = ti.Vector.field(2, ti.f32, N)


#####数据处理

@ti.kernel
def initialize():
    center=ti.Vector([0.5, 0.5])#屏幕范围1*1，左下角是0，0；右上角是1，1；中间是0.5，0.5
    for i in range(N):
        theta = ti.random() * 2 * PI
        r = (ti.sqrt(ti.random()) * 0.7 + 0.3) * galaxy_size#【0.3，1.0】，单纯的距离标量
        offset = r * ti.Vector([ti.cos(theta), ti.sin(theta)])#变成了矢量
        pos[i] = center+offset
        vel[i] = [-offset.y, offset.x]#圆周运动，速度和半径垂直
        vel[i] *= init_vel

@ti.kernel
#一个大kernel中的若干小for循环，编译的时候会被拆分成若干的小kernel
def compute_force():

    # clear force
    #首先，把每个物体受力清0
    for i in range(N):
        force[i] = ti.Vector([0.0, 0.0])

    # compute gravitational force
    for i in range(N):
        p = pos[i]

        #这下面的两个for循环，结果完全一样，但是效率不同

        #两两比赛的那种，换了个方向而已，原来是向后，现在是向前
        #用牛三的相互作用，省了一半
        for j in range(i): # bad memory footprint and load balance, but better CPU performance
            diff = p-pos[j]
            r = diff.norm(1e-5)

            #万有引力公式。**3表示3次方
            # gravitational force -(GMm / r^2) * (diff/r) for i
            f = -G * m * m * (1.0/r)**3 * diff

            #牛顿第三定律，力的作用是相互的
            # assign to each particle
            force[i] += f
            force[j] += -f

        # for j in range(N):# double the computation for a better memory footprint and load balance
        #     if i != j: 
        #         diff = p-pos[j]
        #         r = diff.norm(1e-5)

        #         # gravitational force -(GMm / r^2) * (diff/r) for i
        #         f = -G * m * m * (1.0/r)**3 * diff

        #         # assign to each particle
        #         force[i] += f

@ti.kernel
#有了力以后，就可以更新位置了
def update():
    dt = h/substepping#10/10=1
    for i in range(N):
        #symplectic euler
        vel[i] += dt*force[i]/m
        pos[i] += dt*vel[i]

gui = ti.GUI('N-body problem', (512, 512))

initialize()
while gui.running:#死循环

    for i in range(substepping):
        compute_force()
        update()
    #十六进制，2+2+2，对应8*8*8的RGB颜色值,clear,背景颜色
    gui.clear(0x112F41)
    #绘制圆球，代表行星。field得转成numpy才能传
    gui.circles(pos.to_numpy(), color=0xffffff, radius=planet_radius)
    gui.show()

两个for循环的比较

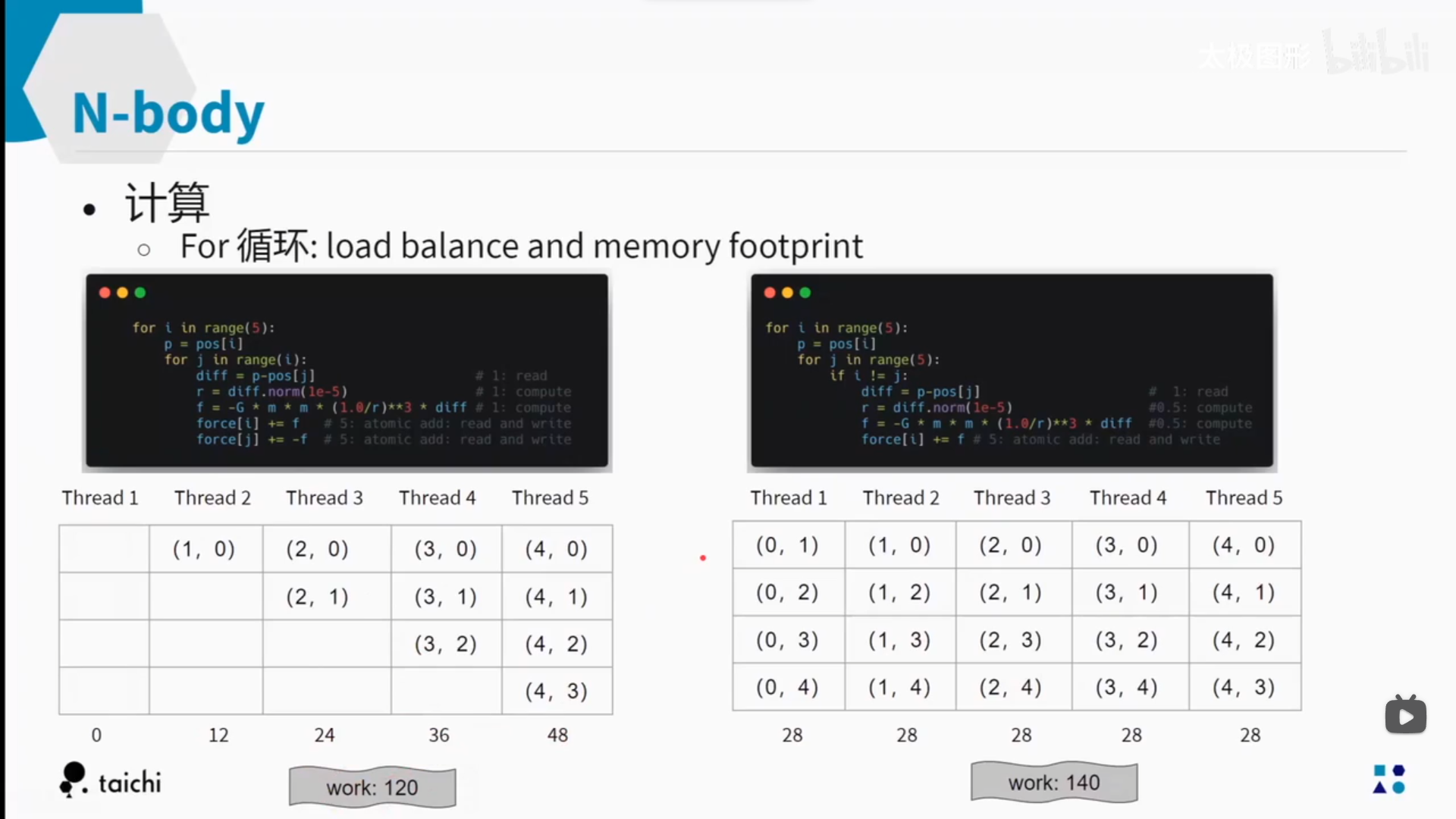
 右边的那个，在GPU上比较快，因为5个并行的线程，负担是平均的。

左边的那个，在CPU上比较快，因为work数稍微小一点。

具体问题具体分析呐……

这里面一个白点，表示一个行星……若干行星在万有引力的相互作用下进行运动……高中物理……我也只会高中物理里简单的一部分。