本文介绍了TaiChi编程语言，其特点包括友好的学习曲线、短小高效的代码、跨平台支持、针对带宽和性能优化。通过实例展示了如何使用简单算术创建虚拟世界，并讲解了数据类型、计算核、并行与原子操作等核心概念。
TaiChi编程语言
A DSL for Computer Graphics
- Productivity
Friendly learning curve
Shorter code, higher perf. - Portability
Multi-backend support - Performance
Optimized for bandwidth, locality and load balancing
只用最基本的加减乘除，每个人都可以通过编程创造一个虚拟世界 ----TaiChi
安装太极编程语言
Python3 -m pip install taichi
安装成功后，直接创建python文件，将其作为包导入即可
太极示例代码：
import taichi as ti
ti.init(arch=ti.gpu)
n = 320
pixels = ti.field(dtype=float, shape=(n * 2, n))
@ti.func
def complex_sqr(z):
return ti.Vector([z[0]**2 - z[1]**2, z[1] * z[0] * 2])
@ti.kernel
def paint(t: float):
for i, j in pixels: # Parallelized over all pixels
c = ti.Vector([-0.8, ti.cos(t) * 0.2])
z = ti.Vector([i / n - 1, j / n - 0.5]) * 2
iterations = 0
while z.norm() < 20 and iterations < 50:
z = complex_sqr(z) + c
iterations += 1
pixels[i, j] = 1 - iterations * 0.02
gui = ti.GUI("Hello World", res=(n * 2, n))
for i in range(1000000):
paint(i * 0.03)
gui.set_image(pixels)
gui.show()import taichi as ti
ti.init(arch=ti.gpu)
n = 320
pixels = ti.field(dtype=float, shape=(n * 2, n))
@ti.func
def complex_sqr(z):
return ti.Vector([z[0]**2 - z[1]**2, z[1] * z[0] * 2])
@ti.kernel
def paint(t: float):
for i, j in pixels: # Parallelized over all pixels
c = ti.Vector([-0.8, ti.cos(t) * 0.2])
z = ti.Vector([i / n - 1, j / n - 0.5]) * 2
iterations = 0
while z.norm() < 20 and iterations < 50:
z = complex_sqr(z) + c
iterations += 1
pixels[i, j] = 1 - iterations * 0.02
gui = ti.GUI("Hello World", res=(n * 2, n))
for i in range(1000000):
paint(i * 0.03)
gui.set_image(pixels)
gui.show()
实现效果：
实时在线运行程序： https://zoo.taichi.graphics/
太极的helloworld
import taichi as ti
ti.init(arch=ti.gpu)
# 以上两行是必须要写在程序前面的，其中init()是必须的
# arch=ti.gpu表示使用GPU运算，如果不指定arch，默认是使用CPU运算
具体支持的硬件接口有：
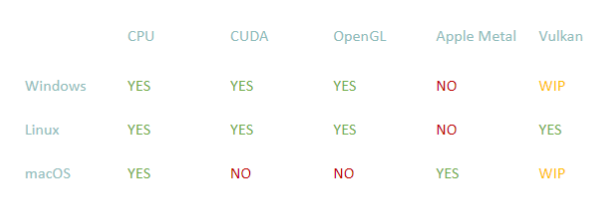
Taichi-scope v.s. Python-scope
就是指的代码的运行环境，代码的运行是否要经过taichi的高性能运算
例子如下：
-
仅仅在python环境下运行：
Everything in a normal Python script is in the Python-scope
import taichi as ti ti.init(arch=ti.cpu) def foo(): print('hello') foo()上方的代码就和基本的python代码并没有什么区别
-
使用TaiChi高性能计算环境
Everything decorated by @ti.kernel or @ti.func is in the Taichi-scope
import taichi as ti ti.init(arch=ti.gpu) @ti.kernel # 声明一个taichi的kernel函数 def foo(): print('hello') foo()当一个函数前面被@ti.kernel修饰时，这个函数就是一个taichi的kernel函数，这个函数就是一个高性能的计算函数.
太极的数据类型
分类
- signed integers: ti.i8, ti.i16, ti.i32, ti.i64 (整型8位，16位，32位，64位)
- unsigned integers: ti.u8, ti.u16, ti.u32, ti.u64 (无符号整型8位，16位，32位，64位)
- floating points: ti.f32, ti.f64 (浮点型32位，64位)
具体可以看如下表格:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hlHlnBBw-1651220151861)(https://cdn.jsdelivr.net/gh/NEUQer-xing/Markdown_images/images/20220429105853.png)]
默认的数据类型:
- ti.f32
- ti.i32
当然,默认的数据类型是支持在init函数中修改的,具体操作如下:
ti.init(default_fp=ti.f32) # float = ti.f32
ti.init(default_fp=ti.f64) # float = ti.f64
ti.init(default_ip=ti.i32) # int = ti.i32
ti.init(default_ip=ti.i64) # int = ti.i64
注意:太极的数据类型之间存在隐式转换
也就是说,当一个变量被定义了之后,它的类型就是固定的了
可以看以下示例:如果a被定义为1,则此时的a的类型就是int32位的,那么当a再次被赋值为2.8888时,太极将会自动将2.8888转换为int32位的整数,也就是2
import taichi as ti
ti.init(arch=ti.gpu)
@ti.kernel
def foo():
a = 1
print("此时的a为",a)
a = 2.8888
print("更改之后的a为",a)
a = 1
b = 1.7
c = a + b
print("f32+i32=",c)
foo()
结果如下:
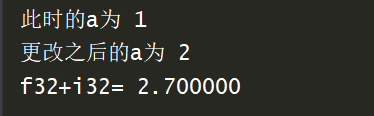
将不同的数据类型做转换: 利用ti.cast()函数
import taichi as ti
ti.init(arch=ti.cpu)
@ti.kernel
def foo():
a = 1.7
b = ti.cast(a, ti.i32)
c = ti.cast(b, ti.f32)
print("b =", b) # b = 1
print("c =", c) # c = 1.0
foo()
结果如下:
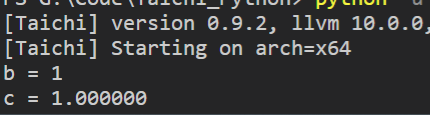
复合类型
复合类型是指一个数据类型包含了多个数据类型的组合,比如:在太极中主要有1.向量2.矩阵3.结构体
- 向量: ti.Vector(n)
- 矩阵: ti.Matrix(n, m)
- 结构体: ti.Struct(...)
方法一:
import taichi as ti
ti.init(arch=ti.cpu)
vec3f = ti.types.vector(3, ti.f32)
# 定义一个3维向量类型,其中每个元素类型是float32位
mat2f = ti.types.matrix(2, 2, ti.f32)
# 定义一个2×2矩阵类型,其中每个元素类型是float32位
ray = ti.types.struct(ro=vec3f, rd=vec3f, l=ti.f32)
# 定义一个结构体类型来表示光线,其中包含2个三维向量来分别表示光线的起始点和光线射出的方向然后和一个浮点数来表示光线的长度
@ti.kernel
def foo():
a = vec3f(0.0)
print(a) # [0.0, 0.0, 0.0]
d = vec3f(0.0, 1.0, 0.0)
# 使用三维向量类型来创建一个三维向量对象
print(d) # [0.0, 1.0, 0.0]
B = mat2f([[1.5, 1.4], [1.3, 1.2]])
# 使用二维矩阵类型来创建一个二维矩阵对象
print("B =", B) # B = [[1.5, 1.4], [1.3, 1.2]]
r = ray(ro=a, rd=d, l=1)
# 使用结构体类型来创建一个结构体对象
print("r.ro =", r.ro) # r.ro = [0.0, 0.0, 0.0]
print("r.rd =", r.rd) # r.rd = [0.0, 1.0, 0.0]
foo()
方式二:
mport taichi as ti
ti.init(arch=ti.cpu)
@ti.kernel
def foo():
a = ti.Vector([0.0, 0.0, 0.0])
# 直接使用ti.Vector()来创建一个三维向量对象
print(a) # [0.0, 0.0, 0.0]
d = ti.Vector([0.0, 1.0, 0.0])
print(d) # [0.0, 1.0, 0.0]
B = ti.Matrix([[1.5, 1.4], [1.3, 1.2]])
# 直接使用ti.Matrix()来创建一个二维矩阵对象
print("B =", B) # B = [[1.5, 1.4], [1.3, 1.2]]
r = ti.Struct(v1=a, v2=d, l=1)
print("r.v1 =", r.v1) # r.v1 = [0.0, 0.0, 0.0]
print("r.v2 =", r.v2) # r.v2 = [0.0, 1.0, 0.0]
foo()
可以直接利用ti.Vector和ti.Matrix来定义向量和矩阵,而ti.Struct则是用来定义结构体
ti.field ---- a global N-d array of elements
• global: can be read/written from both the Taichi-scope and the Python-scope
• N-d: (Scalar: N=0), (Vector: N=1), (Matrix: N=2), (N = 3, 4, 5, …)
• elements: scalar, vector, matrix, struct
结合具体的代码来理解吧:
import taichi as ti
ti.init(arch=ti.cpu)
pixels = ti.field(dtype=float, shape=(16, 8))
pixels[1, 2] = 42.0
print(pixels[1, 2]) # 42.0
这里定义的是一个16×8的field,也就是说这个field中包含了16×8个元素,每个元素的类型一个float元素
我的理解是这个样的:
import taichi as ti
ti.init(arch=ti.cpu)
vf = ti.Vector.field(3, ti.f32, shape=4)
@ti.kernel
def foo():
v = ti.Vector([1, 2, 3])
vf[0] = v
print(vf[0]) # [1.0, 2.0, 3.0]
foo()
这个是定义的一个4×1大小的field,也就是说这个field中包含了4个元素,每个元素都是一个3维向量,每个三维向量中的元素类型是float32
我的理解是这样:
特别的:access a zero-d field using [None]
例如:
zero_d_scalar = ti.field(ti.f32, shape=())
zero_d_scalar[None] = 1.5
zero_d_vec = ti.Vector.field(2, ti.f32, shape=())
zero_d_vec[None] = ti.Vector([2.5, 2.6])
可以再试着理解一下这几个例子,应该就可以理解field了
•“3D gravitational field in a 256x256x128 room”
gravitational_field = ti.Vector.field(n = 3,dtype=ti.f32,shape=(256,256,128))
•“2D strain-tensor field in a 64x64 grid”
strain_tensor_field = ti.Matrix.field(n = 2,m = 2,dtype=ti.f32, shape=(64,64))
•“a global scalar that I want to access in a Taichi kernel”
global_scalar = ti.field(dtype=ti.f32, shape=())
太极的计算核
串行与并行
首先,假想一个问题:
可以明显的看到,虽然CPU的单个核心的能力比较强,但是,在人多力量大面前,也是自愧不如的,因为图形学大部分计算都是相同的,所以可以去让每个点对应的计算去并行进行,从而提高计算速度
kernel == cuda _global_
我现在理解到的kernel就是整个太极优化的核心部分,在这个kernel下面的函数中,如果存在for循环的话,而且该for循环是位于第一层,Taichi会将其在编译时,将其分给多个并行的核心去执行该循环,从而提高计算速度,但是如果该循环不是在第一层,那么,它将仍然会以串行的方式去执行,比如下面的示例代码:
@ti.kernel
def fill():
for i in range(10):
# 在第一层,所以该层的所有操作均会被并行执行
# 可以理解为,本次总共有10个重复的大操作
# 所以,taichi将会把这10个分成10份,分别交给1个gpu核心去运算
x[i] += i
s = 0
for j in range(5):
# 在第二层,因为这是已经被分配到核心的具体任务了
# 所以,这里的操作只会被一个核心去执行
# 因此,这里的操作只能是串行执行的,而不是并行的
s += j
y[i] = s
同时,应该注意,如果在一个kernel下的函数有多个第一层for循环,那么每个第一层for循环都是会被并行执行的
但是,在每个第一层for循环之间,它们是串行执行的,可以看一下代码:
import taichi as ti
ti.init(arch=ti.gpu)
a = ti.field(ti.f32, shape=())
@ti.kernel
def foo():
for i in range(10):
# 第一层,分配10个核心去执行
a[None] += 1
# 等结束之后,回收10个核心
print("第一个for循环后结果:",a[None])
for i in range(10):
# 第一层,再分配这10个核心去执行
a[None] += 2
# 等结束之后,回收10个核心
print("第二个for循环后结果:",a[None])
for i in range(10):
# 第一层,再再分配这10个核心去执行
print(a[None])
# 等结束之后,回收10个核心
print("第三个for循环后结果:",a[None])
foo()
输出结果如图:
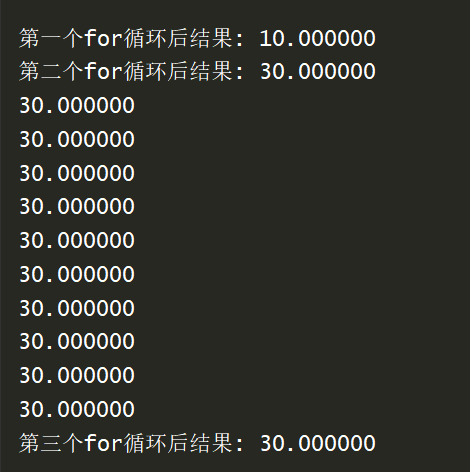
可以很清楚的看到同是第一层的for之间是串行执行的
我们将上述代码做如下修改:
import taichi as ti
ti.init(arch=ti.gpu)
a = ti.field(ti.f32, shape=())
@ti.kernel
def foo():
for i in range(100):
# 第一层,分配10个核心分别去执行10个任务,每完成一次,就输出一次
# 可以看到,这10个任务是并行的,
# 也就是说,输出的结果将会是无序的
a[None] += 1
print("第一次for的第",i,"次加法,结果为:",a[None])
print("第一个for循环后结果:",a[None])
for i in range(10):
a[None] += 2
print("第二个for循环后结果:",a[None])
for i in range(10):
print(a[None])
print("第三个for循环后结果:",a[None])
# 但最后输出的结果肯定会是正确的
foo()
执行结果如图:
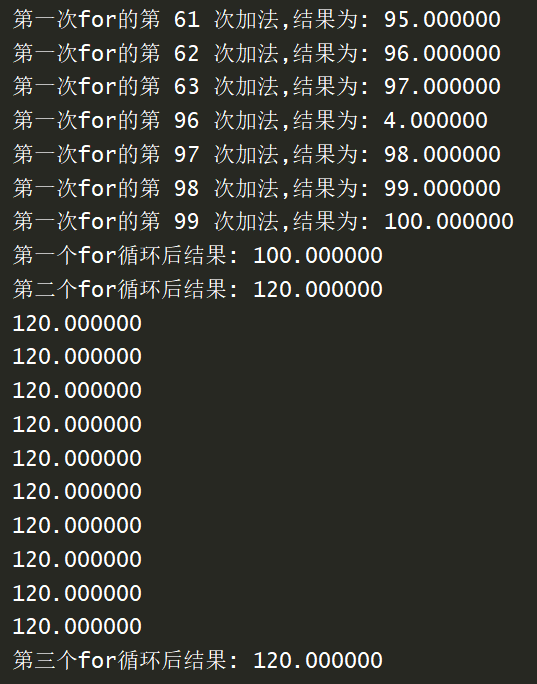
理解这个之后,如果我们想把第二层的for进行并行执行,那我们可以进行如下操作:
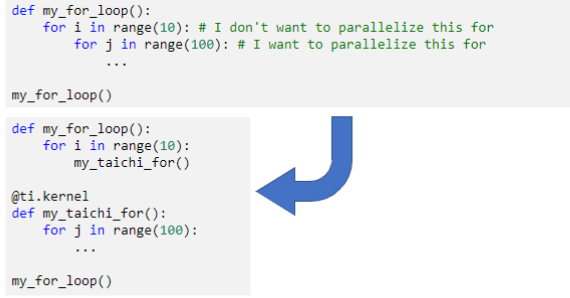
将想要并行的for写进kernel函数中,然后在kernel函数中进行并行执行,把第一层的for留在外面
注意,由于第一层for是并行的,所以,我们无法在某个核心中将其break掉
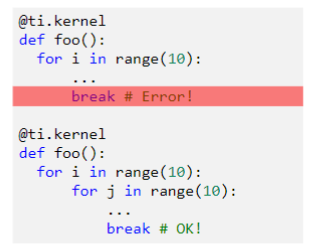
这里还有一个问题,就是并行虽然可以提高速度,但是,对于数据我们无法保证它们是同步的,也就是说,可能每个核心在将要做任务时,现在已经有核心在做了,这明显就会引起重复的任务,导致最后结果不正确(其实,这个和操作系统的进程之间的关系有点类似)
拿下面举例:
加法操作为: a[None] = a[None] + 1
这个可以看成3部分:
第一,取得这个原始值
第二,对其进行加一操作
第三,写回对应的地址
比如:
import taichi as ti
ti.init(arch=ti.gpu)
a = ti.field(ti.f32, shape=())
@ti.kernel
def foo():
for i in range(10):
a[None] = a[None] + 1
print("这是第",i,"次的结果:",a[None])
print("这是最终的结果:",a[None])
foo()
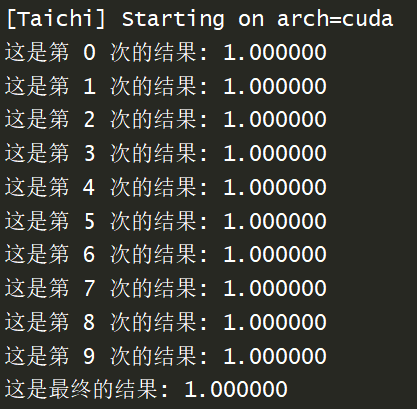
可以看到每个核心都只做了一次最初始数的操作,也就是说,每个核心并没有意识到其实已经有人在做了,他自己又拿最初的数做一遍,所以结果肯定是不正确的
但,如何解决呢,我们可以定义原子操作,也就是将其三步变成一步,这样,当一个核心已经开始进入原来逻辑的第一步时,其它核心就不可以操作,这样就保证了原子操作的正确性
import taichi as ti
ti.init(arch=ti.gpu)
a = ti.field(ti.f32, shape=())
@ti.kernel
def foo():
for i in range(100):
a[None] += 1
print("这是第",i,"次的结果:",a[None])
print("这是最终的结果:",a[None])
foo()
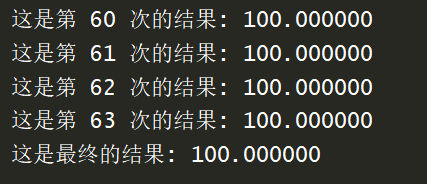
可以看到,结果是正确的,同时,输出也是无序的,说明,原子操作之外的操作,仍是并行执行的
比如最后一行可以解释为:当第63号核心做完它的第一个原子操作时,再想回头输出看看结果时,发现其它核心已经在它想看的这个间隙中,将结果做完了,所以会输出100
以上就是串行并行原子操作等的解释了
然后就是,kernel还要注意几点:
第一,传入的参数要指定类型
import taichi as ti
ti.init(arch=ti.cpu)
@ti.kernel
def my_kernel(x: ti.i32, y: ti.f32):
print(x + y)
my_kernel(2, 3.3) # 5.3
第二,向量要分解成单个再传入
import taichi as ti
ti.init(arch=ti.cpu)
@ti.kernel
def bad_kernel(v: ti.Vector):# 错误
...
@ti.kernel
def good_kernel(vx: ti.f32, vy: ti.f32):#正确
v = ti.Vector([vx, vy])
...
第三,与c++类似,它不会对传入的参数做值的变化
import taichi as ti
ti.init(arch=ti.cpu)
@ti.kernel
def foo(x: ti.i32):
x = x + 1
print("x in foo:", x) # 101
x = 100
foo(x)
print("x outside foo:", x) # 100
如果想要可以变化,就和c++一样,使用全局变量:在这里是ti.field()
func
可以基本理解为宏定义,就是将重复的代码部分写进一个函数,当调用函数时,相当于把代码再还原回去
所以,该函数也就不能支持递归操作了
import taichi as ti
ti.init(arch=ti.cpu)
@ti.func
def my_func(x):
x = x + 1
print("x in my func:", x) # 234
@ti.kernel
def my_kernel():
x = 233
my_func(x)
print("x outside my func:", x) # 233
my_kernel()
kernel func python 之间调用关系
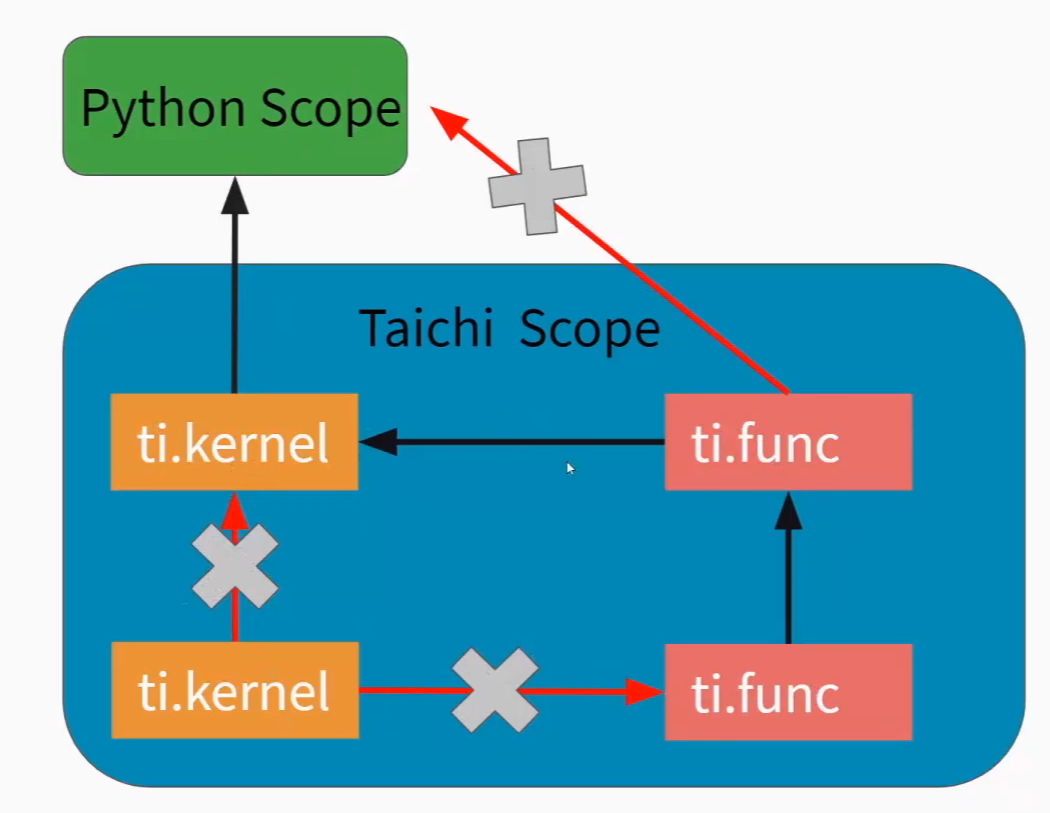
ops
可视化 gui
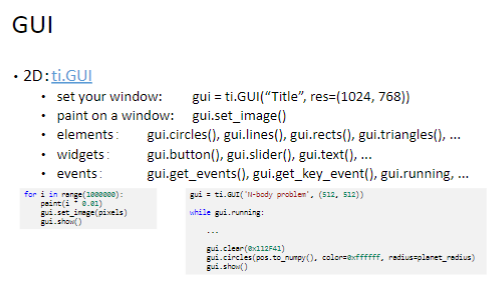
先来看一下效果吧
GPU下运行:
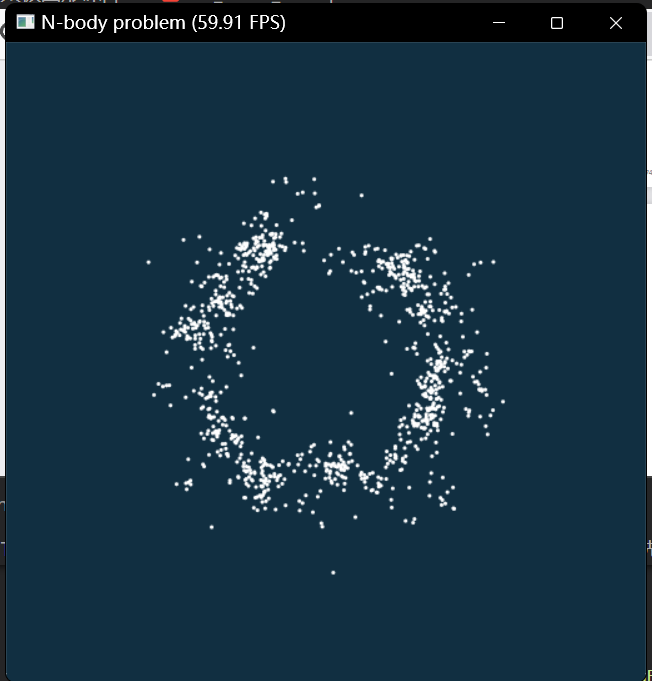
CPU下运行:
上面的FPS说明了一切
扫一扫
852
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
