Mathematica的学习打卡day 11

Mathematica的学习打卡day 11

————太原理工大学机器人团队

今天的学习内容为级数（学习来源为哔哩哔哩）

Series级数

可以将函数按照泰勒级数的定义进行展开，同时也可以应用于多元函数的泰勒展开，如同先前提到的微积分一样，多元函数的级数展开，也是先要展开后面未知数的，用法Series[函数，{x（变量），某点，最高展开的幂}]。。

还可以处理未知的某点的函数展开式。。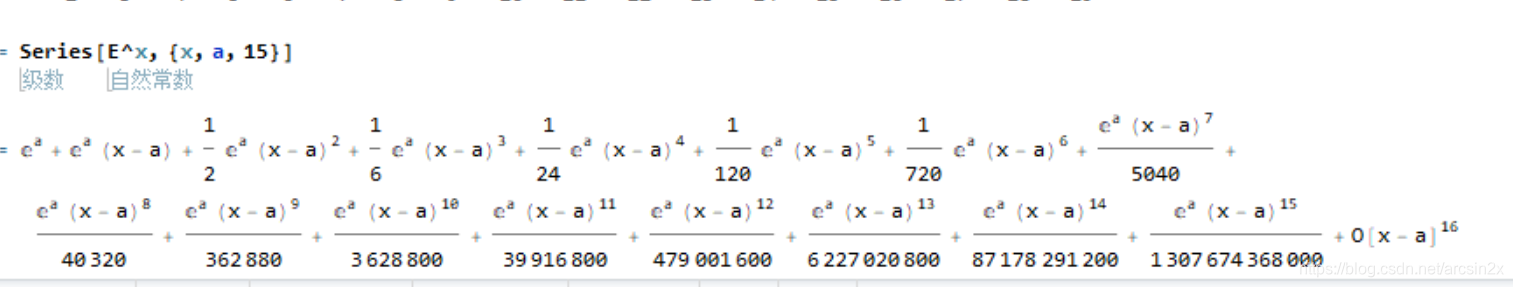

这个是多元函数的展开。。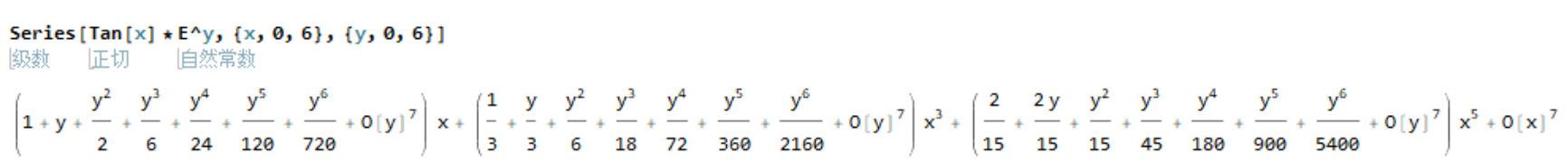

这里需要说明一下，函数的变量的指数或者一些初等函数的一些形式，会使Mathematica判定这一项本身就是展开式的一部分，只会将所要的最高次幂按照告诫无穷小的形式输出（这可能软件仍有一些瑕疵吧）。。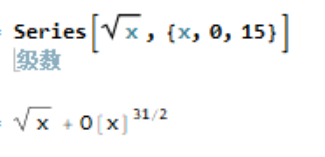

幂级数的求和

Sum[函数，{i，min，max，步长（省略时为1）}]，当级数收敛时我们可以得到函数的最终表达式或者具体的数字，若函数发散，我们只能得到函数的一个传统的和式.。。

幂级数的系数

我们有时更为关注函数的系数，那么我们用SeriseCoeffient[函数，{变量，展开点，幂}]。。

傅里叶级数

傅里叶级数是另一种的级数展开形式。。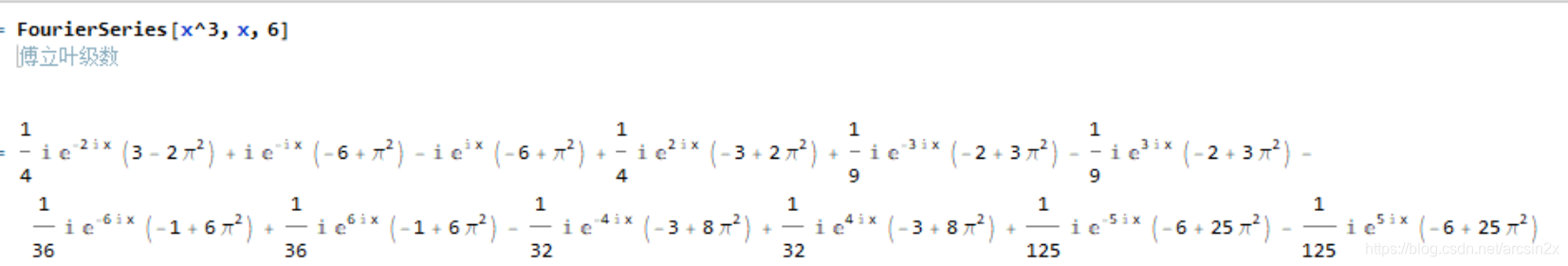

今天的内容就到这里，如有错误欢迎斧正