【2-SAT】【树链剖分】【线段树】【前缀和优化建图】CF1007D Ants

最新推荐文章于 2023-09-25 23:08:33 发布

原创

最新推荐文章于 2023-09-25 23:08:33 发布 · 451 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #2-SAT #树链剖分 #线段树 #前缀和优化建图

该博客介绍了如何利用树链剖分和线段树优化解决二选一的2-SAT问题。在给定一棵树和多次染色操作的情况下，通过建图和Tarjan算法判断是否存在不重复染色的方案。文章详细阐述了建图过程、树的遍历方法以及线段树的更新策略，最后给出了完整的C++代码实现。

题意

给定一棵树，开始每条边都没有颜色
有m次操作，每次给定两个点对 $(a, b)$ $(c, d)$ ，选择一个给两者的路径上的边染色
问是否存在一种选择方式，使得不存在被重复染色的边

分析

考虑这种二选一的需要2-SAT解决
重点在于降低建图的复杂度

利用树链剖分和线段树实现路径染色
那么我们要求就是线段树上存在儿子祖先关系的点不能同时选择

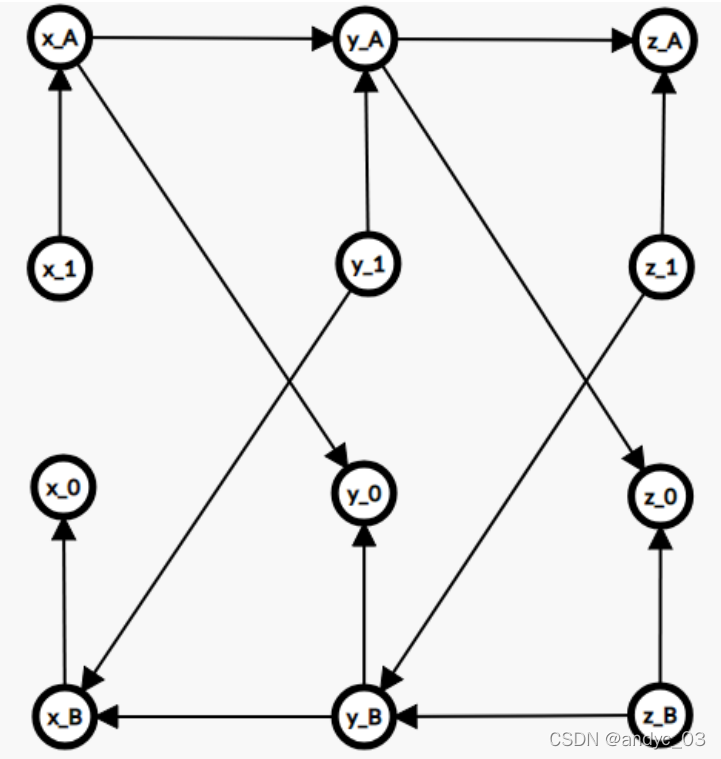
这里用到了前缀和优化建图
最上方一行和最下方一行为辅助节点，这样保证了点数是 $O(nlog^2n)$ 级别的，降低了复杂度

在这里插入图片描述

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e5+5;
int n,top[maxn],siz[maxn],son[maxn];
vector <int> G[maxn];
int m,seg[maxn];
int f[maxn],dep[maxn];
void dfs(int u,int fa)
{
   
   
    siz[u]=1; dep[u]=dep[fa]+1; f[u]=fa;
    for(auto to:G[u])
    {
   
   
        if(to==fa) continue;
        dfs(to,u);
        siz[u]+=siz[to];
        if(siz[to]>siz[son[u]]) son[u]=to;
    }
}
void ddfs(int u,int fa)
{
   
   
    top[u]=fa; seg[u]=++seg[0];
    if(son[u])
    {
   
   
        ddfs(son[u],fa)