【莫比乌斯反演】【整除分块】【期望】随机添数-优快云博客

本文链接：https://blog.youkuaiyun.com/andyc_03/article/details/122973544

本文探讨了在一系列随机生成的1到m（m≤1e5）之间整数的序列中，其GCD（最大公约数）为1的平均序列长度。通过数学分析和代码实现，提供了求解这个问题的方法，并讨论了其计算策略。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题意

给定一个初始为空的序列，每次随机添加一个1-m之间的数，求整个序列的 gcd 为 1 的期望长度

T次询问 T,m<=1e5

分析

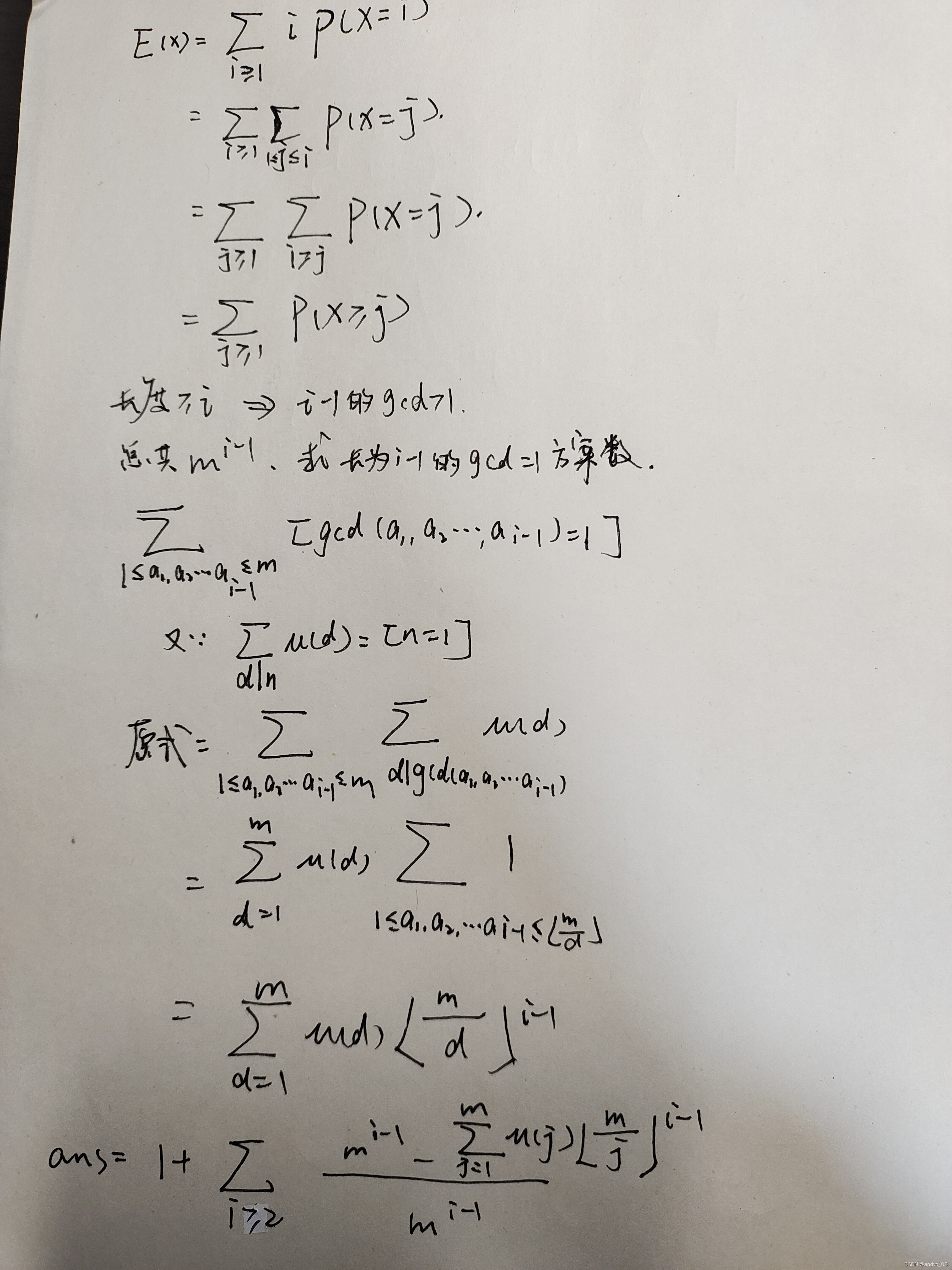
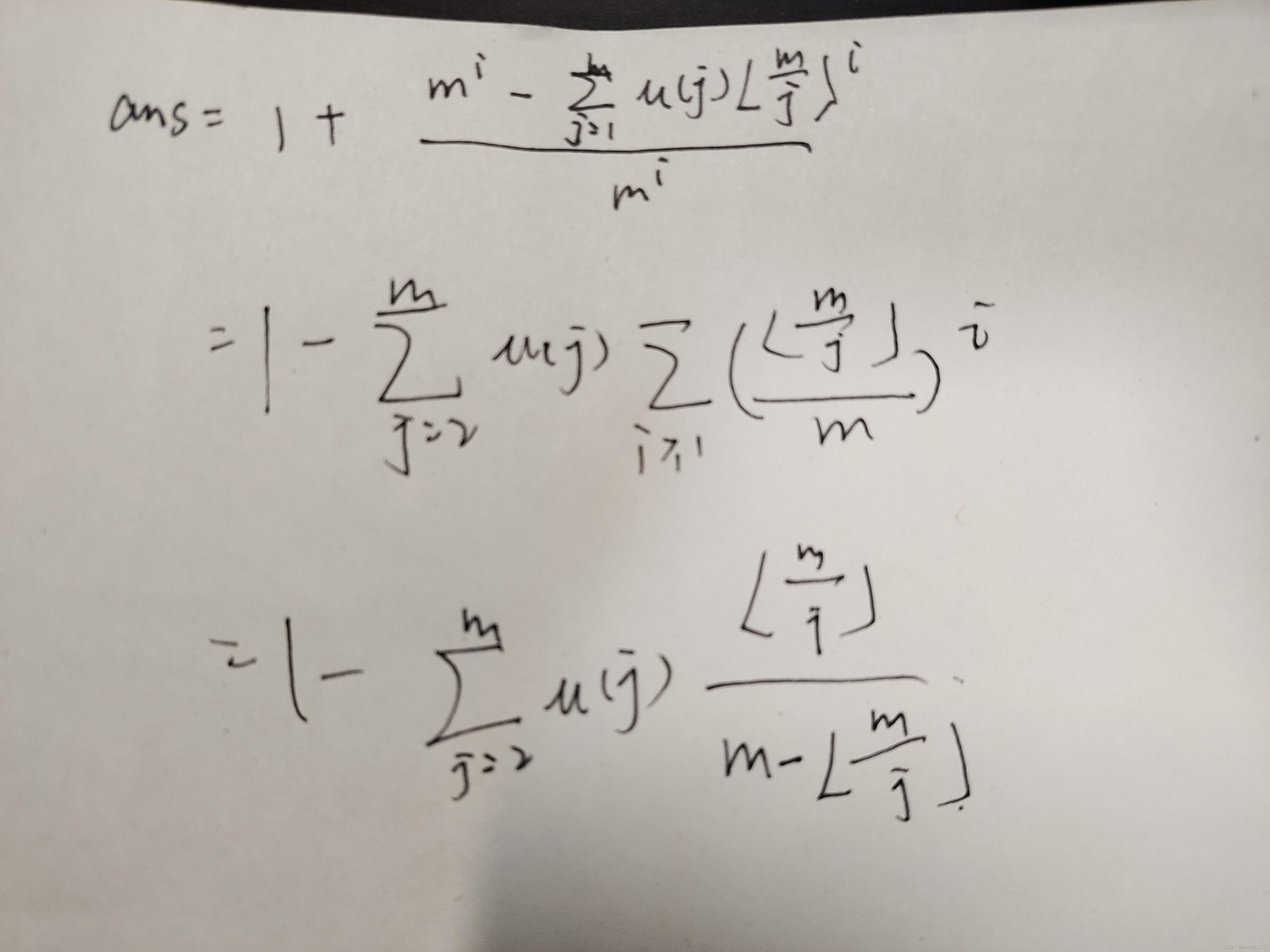
代码

轻微卡常

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e5+5;
const int mod=1e9+7;
bool vis[maxn];
int m,cnt,p[maxn];
ll inv[maxn],f[maxn],mu[maxn];
char buf[1<<23],*p1=buf,*p2=buf;
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
inline int read()
{
	int s=0;
	char ch=getchar(),last;
	while(ch<'0'||ch>'9') last=ch,ch=getchar();
	while(ch>='0'&&ch<='9') s=(s<<1)+(s<<3)+(ch^48),ch=getchar();
	return last=='-'?-s:s;
}
void init()
{
    mu[1]=inv[0]=inv[1]=1;
    for(int i=2;i<maxn;i++)
    {
        if(!vis[i])
        {
            p[++cnt]=i;
            mu[i]=-1;
        }
        for(int j=1;j<=cnt && i*p[j]<maxn;j++)
        {
            vis[i*p[j]]=1;
            if(i%p[j]==0) break;
            mu[i*p[j]]=-mu[i];
        }
    }
    for(int i=2;i<maxn;i++)
        inv[i]=(mod-mod/i)*inv[mod%i]%mod,mu[i]=(mu[i-1]+mu[i]%mod+mod)%mod;
}
inline void write(ll X)
{
	if(X<0) {X=~(X-1); putchar('-');}
	if(X>9) write(X/10);
	putchar(X%10+'0');
}
int main()
{
    freopen("random.in","r",stdin);
    freopen("random.out","w",stdout);
    init();
    int T;
    scanf("%d",&T);
    ll ans,val;
    while(T--)
    {
        m=read();
        ans=1;
        for(int l=2,r;l<=m;l=r+1)
        {
            val=m/l;
            r=m/val;
            ans=(ans+mod-(mu[r]-mu[l-1])*val%mod*inv[m-val]%mod)%mod;
        }
        write(ans);  putchar('\n');
    } 
    return 0;
}