模运算的基本性质

模运算（Modular Arithmetic）是数论中的一个重要概念，在密码学、计算机科学和工程领域有广泛应用。以下是模运算的主要性质：

基本定义

对于整数a、b和正整数m，我们说a与b模m同余，记作：

a≡b(modm)

当且仅当m整除(a - b)，即存在整数k使得：

a−b=km

基本性质

算术运算性质

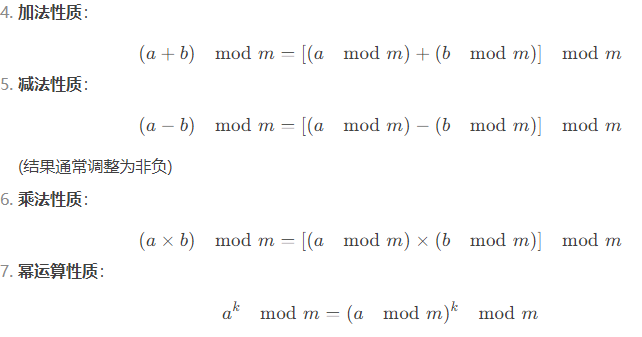
重要定理

模逆元

模逆元定义：

应用实例

模指数运算（快速幂算法）：

def mod_exp(base, exp, mod):
    result = 1
    base = base % mod
    while exp > 0:
        if exp % 2 == 1:
            result = (result * base) % mod
        exp = exp >> 1
        base = (base * base) % mod
    return result

模逆元计算（扩展欧几里得算法）：

def mod_inverse(a, m):
    g, x, y = extended_gcd(a, m)
    if g != 1:
        return None  # 逆元不存在
    else:
        return x % m

模运算的这些性质在密码学（如RSA、Diffie-Hellman）、哈希算法、随机数生成和错误检测编码（如CRC）等领域都有重要应用。