快速幂算法
将模幂运算转换为模乘运算的主要依据是快速幂算法(Exponentiation by Squaring),结合模运算的性质。以下是详细的数学依据和步骤:
1. 模运算的基本性质
- 乘法性质:

这意味着在模运算中,乘法可以分步取模,避免中间结果溢出。 - 幂的展开:
任何指数 e可以表示为二进制形式,例如
从而将幂运算分解为多次平方和乘法。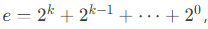
2. 快速幂算法的核心思想
计算 a mod m 时,通过将指数 e 表示为二进制,将问题转化为一系列平方和乘法操作:
- 从最低位到最高位逐位处理指数 e。
- 每次迭代时:
-
- 平方当前基数:
(对应指数位的权重翻倍)。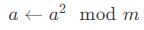
- 如果当前二进制位为1,则乘到结果中:
。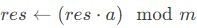
- 平方当前基数:
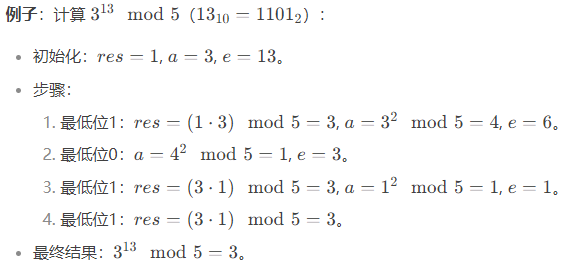
3. 为什么能转为模乘?
- 快速幂算法将幂运算拆解为多个模平方和模乘步骤,每一步的中间结果都通过模运算保持较小规模,避免直接计算大数幂。
- 依赖的数学定理:
-
- 模运算的分配律(如上所述)。
- 二进制分解的合法性(任何整数可唯一表示为二进制)。
模幂转模乘的依据是快速幂算法和模运算的乘法分配律,通过二进制分解指数,将幂运算转化为一系列可模的平方和乘法操作,显著降低计算复杂度(从 O(e)降到 O(loge)





 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 7947
7947

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








