leetcode基础算法教程 #Datawhale

神迹小卒

已于 2024-10-01 17:36:24 修改

阅读量1.2k

点赞数 23

文章标签：算法 leetcode 职场和发展

于 2024-09-17 12:41:50 首次发布

本文链接：https://blog.youkuaiyun.com/aiqq136/article/details/142311415

版权

0917 - TASK1：枚举算法 Enumeration-Algorithm

学习链接

https://github.com/datawhalechina/leetcode-notes/blob/main/docs/ch04/04.01/04.01.01-Enumeration-Algorithm.md

刷题链接

https://github.com/datawhalechina/leetcode-notes/blob/main/docs/ch04/index.md

1. 枚举算法简介

Enumeration Algorithm

穷举：列举所有解，比较，得到满足条件解

优势：编程简单，算法正确容易证明

劣势：大数据情况下，效率低下

2. 枚举算法的解题思路

2.1 枚举算法的解题思路

最基本，最简单，解题优先考虑，再优化

确定枚举对象、枚举范围和判断条件

缩小问题状态空间，加强约束
2.2 枚举算法的简单应用

百钱买百鸡问题：鸡翁一，值钱五；鸡母一，值钱三；鸡雏三，值钱一；百钱买百鸡，则鸡翁、鸡母、鸡雏各几何？

公鸡一只五块钱，母鸡一只三块钱，小鸡三只一块钱。现在我们用 100 块钱买了 100 只鸡，问公鸡、母鸡、小鸡各买了多少只？

公鸡x、母鸡y、小鸡z

5x+3y+z/3=100

x+y+z=0

z%3==0

x,y,z属于[0，100]


class Solution:
    def buyChicken(self):
        for x in range(101):
            for y in range(101):
                for z in range(101):
                    if z % 3 == 0 and 5 * x + 3 * y + z // 3 == 100 and x + y + z == 100:
                        print("公鸡 %s 只，母鸡 %s 只，小鸡 %s 只" % (x, y, z))

提高枚举算法的效率

z=100-x-y：不用再枚举z
但其实如果所有钱用来买公鸡，最多只能买 20只，
同理，全用来买母鸡，最多只能买 33 只。

class Solution:
    def buyChicken(self):
        for x in range(21):
            for y in range(34):
                z = 100 - x - y
                if z % 3 == 0 and 5 * x + 3 * y + z // 3 == 100:
                    print("公鸡 %s 只，母鸡 %s 只，小鸡 %s 只" % (x, y, z))

3. 枚举算法的应用

3.1 两数之和 Two Sum

https://leetcode.cn/problems/two-sum/

Given an array of integers nums and an integer target, return indices of the two numbers such that they add up to target.

You may assume that each input would have exactly one solution, and you may not use the same element twice.

You can return the answer in any order.

Example 1:

Input: nums = [2,7,11,15], target = 9
Output: [0,1]
Explanation: Because nums[0] + nums[1] == 9, we return [0, 1].

Example 2:

Input: nums = [3,2,4], target = 6
Output: [1,2]

Example 3:

Input: nums = [3,3], target = 6
Output: [0,1]
Constraints:

2 <= nums.length <= 104
-109 <= nums[i] <= 109
-109 <= target <= 109
Only one valid answer exists.

Follow-up: Can you come up with an algorithm that is less than O(n2) time complexity?

我的代码1：JAVA

class Solution {
    public int[] twoSum(int[] nums, int target) {
        for(int i = 0; i< nums.length-1; i++){
            for(int j = i+1;j< nums.length;j++){
                if(nums[i]+nums[j]==target){
                    int[] output={i,j};
                    return output;
                }
            }
        }
        return null;
    }
}

参考答案Python

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        for i in range(len(nums)):
            for j in range(i + 1, len(nums)):
                if i != j and nums[i] + nums[j] == target:
                    return [i, j]
        return []

我的代码2：JAVA

class Solution {
    public int[] twoSum(int[] nums, int target) {
        for(int i = 0; i< nums.length-1; i++){
            for(int j = i+1;j< nums.length;j++){
                if(nums[i]+nums[j]==target){
                    int[] output={i,j};
                    return output;
                }
            }
        }
			return new int[0];//改进:应该返回空数组
    }
}

3.2 计数质数

https://leetcode.cn/problems/count-primes/description/
204. Count Primes
Given an integer n, return the number of prime numbers that are strictly less than n.

Example 1:

Input: n = 10
Output: 4
Explanation: There are 4 prime numbers less than 10, they are 2, 3, 5, 7.

Example 2:

Input: n = 0
Output: 0

Example 3:

Input: n = 1
Output: 0

Constraints:

0 <= n <= 5 * 106

素数，质数(只能被1和其自身整除);

我的第一次代码：JAVA

class Solution {
    public int countPrimes(int n) {
        if (n<=2){
            return 0;
        }
        int primeNumsCount = 0;
        for (int i = 2; i < n; i++) {
            boolean isPrime = true;
            for (int j = 2; j <= Math.sqrt(i); j++) { //每个合成数（非质数）的因数总是成对出现的，3.16
                if (i % j == 0) {
                    isPrime = false;
                    break;
                } 
            }
            if (isPrime) {
                primeNumsCount++;
            }
        }
        return primeNumsCount;
    }
}

超出时间限制，n=1500000

参考答案Python：超时

class Solution:
    def isPrime(self, x):
        for i in range(2, int(pow(x, 0.5)) + 1):
            if x % i == 0:
                return False
        return True

    def countPrimes(self, n: int) -> int:
        cnt = 0
        for x in range(2, n):
            if self.isPrime(x):
                cnt += 1
        return cnt

Improve：我的代码JAVA
当 n 很大时，当前算法在每个数上都进行了一次质数检查，
而这个检查的时间复杂度是 O(sqrt(i))，对于大输入来说不够高效。
埃拉托色尼筛法（Sieve of Eratosthenes）
算法的时间复杂度是
在这里插入图片描述
核心思想是，通过标记非质数来筛选出质数
创建一个大小为 n 的布尔数组 isPrime，初始化为全 true，其中 isPrime[i] 表示 i 是否为质数。
从 2 开始，如果 i 是质数，那么将 i 的所有倍数标记为非质数。
遍历整个数组，剩下未被标记为非质数的数就是质数。

class Solution {
    public int countPrimes(int n) {
        if (n <= 2) {
            return 0;
        }

        // 创建一个布尔数组，表示从0到n-1每个数是否是质数
        boolean[] isPrime = new boolean[n];
        for (int i = 2; i < n; i++) {
            isPrime[i] = true;
        }

        // 使用埃拉托色尼筛法标记所有非质数
        for (int i = 2; i * i < n; i++) {
            if (isPrime[i]) {
                for (int j = i * i; j < n; j += i) {
                    isPrime[j] = false;
                }
            }
        }

        // 统计质数的数量
        int primeNumsCount = 0;
        for (int i = 2; i < n; i++) {
            if (isPrime[i]) {
                primeNumsCount++;
            }
        }

        return primeNumsCount;
    }
}

3.3 统计平方和三元组的数目 Count Square Sum Triples

A square triple (a,b,c) is a triple where a, b, and c are integers and a^2 + b^2 = c^2.

Given an integer n, return the number of square triples such that 1 <= a, b, c <= n.

Example 1:

Input: n = 5
Output: 2
Explanation: The square triples are (3,4,5) and (4,3,5).

Example 2:

Input: n = 10
Output: 4
Explanation: The square triples are (3,4,5), (4,3,5), (6,8,10), and (8,6,10).

Constraints:

1 <= n <= 250

我的第一次代码：JAVA

class Solution {
    public int countTriples(int n) {
        int count = 0;
        for (int c = n; c >= 1; c--) {
            for (int a = 1; a < c; a++){
                for(int b =1 ; b < c; b++){
                    if(a*a+b*b==c*c){
                        count++;
                    }
                }
            }
        }
        return count;
    }
}

参考代码python

class Solution:
    def countTriples(self, n: int) -> int:
        cnt = 0
        for a in range(1, n + 1):
            for b in range(1, n + 1):
                c = int(sqrt(a * a + b * b + 1))
                if c <= n and a * a + b * b == c * c:
                    cnt += 1
        return cnt

优化：可以减少复杂度，改为两个循环
cnt = 0
for a in range(1, n + 1): # 遍历 a 从 1 到 n
for b in range(1, n + 1): # 遍历 b 从 1 到 n
c = int(sqrt(a^2 + b^2)) # 计算 c 的平方根并取整
if c <= n and c^2 == a^2 + b^2: # 检查 c 是否符合条件
cnt += 1 # 如果符合条件，计数加 1

class Solution {
    public static int countTriples(int n) {
        int count = 0;
        // 遍历 a 从 1 到 n
        for (int a = 1; a <= n; a++) {
            // 遍历 b 从 1 到 n
            for (int b = 1; b <= n; b++) {
                // 计算 c^2 = a^2 + b^2
                int cSquare = a * a + b * b;
                // 取 c 的平方根并取整
                int c = (int) Math.sqrt(cSquare);
                
                // 检查是否是整数平方且 c 在 [1, n] 范围内
                if (c <= n && c * c == cSquare) {
                    count++;
                }
            }
        }
        return count;
    }
}

0919 - TASK1：Exercises：Write the three questions

0.Links

相关学习链接：https://github.com/datawhalechina/leetcode-notes/blob/main/docs/ch04/04.02/04.02.01-Recursive-Algorithm.md

网址链接：
https://github.com/datawhalechina/leetcode-notes/blob/main/docs/ch04/index.md

1. 2427. Number of Common Factors公因子的数目

LINK: https://leetcode.cn/problems/number-of-common-factors/description/

Given two positive integers a and b, return the number of common factors of a and b.

An integer x is a common factor of a and b if x divides both a and b.

Example 1:

Input: a = 12, b = 6
Output: 4
Explanation: The common factors of 12 and 6 are 1, 2, 3, 6.

Example 2:

Input: a = 25, b = 30
Output: 2
Explanation: The common factors of 25 and 30 are 1, 5.

Constraints:

1 <= a, b <= 1000

Solution

think about the Enumeration Algorithm
start with the example: from input to output, write it down in ipad

在这里插入图片描述

java

class Solution {
    public int commonFactors(int a, int b) {
        int count = 0;
        for(int i = 1; i <=(a>b?b:a);i++){
            if((a%i==0) && (b%i==0)){
                count++;
            }
        }
        return count;
    }
}

在这里插入图片描述

Datawhale python

最直接的思路就是枚举所有 [ 1 , m i n ( a , b ) ] 之间的数，并检查是否能同时整除 a 和 b 。

当然，因为 a 与 b 的公因子肯定不会超过 a 与 b 的最大公因数，则我们可以直接枚举 [ 1 , g c d ( a , b ) ] 之间的数即可，其中 g c d ( a , b ) 是 a 与 b 的最大公约数。

class Solution:
    def commonFactors(self, a: int, b: int) -> int:
        ans = 0
        for i in range(1, math.gcd(a, b) + 1):
            if a % i == 0 and b % i == 0:
                ans += 1
        return ans

Improve

1.Greatest Common Divisor

    // 递归计算 a 和 b 的最大公约数
    public static int gcd(int a, int b) {
        if (b == 0) {
            return a;
        }
        return gcd(b, a % b);
    }

2.以 gcd(48, 18) 为例，来看看递归过程是如何工作的。

第一次调用：gcd(48, 18)
    b != 0，所以继续调用 gcd(18, 48 % 18)，即 gcd(18, 12)。

第二次调用：gcd(18, 12)
    b != 0，继续调用 gcd(12, 18 % 12)，即 gcd(12, 6)。

第三次调用：gcd(12, 6)
    b != 0，继续调用 gcd(6, 12 % 6)，即 gcd(6, 0)。

第四次调用：gcd(6, 0)
    b == 0，终止递归，返回 6，即 gcd(48, 18) 的结果是 6。

Why gcd(a, b) == gcd(b, a % b)
欧几里得算法（Euclidean algorithm）
通过 gcd(a, b) 转化为 gcd(b, a % b)，即用较小的余数代替较大的数，直到其中一个数为 0。
### java-version2

class Solution {
    public static int gcd(int a, int b) {
        if (b == 0) {
            return a;
        }
        return gcd(b, a % b);
    }

    public int commonFactors(int a, int b) {
        int count = 0;
        for(int i = 1; i <=gcd(a,b);i++){
            if((a%i==0) && (b%i==0)){
                count++;
            }
        }
        return count;
    }


}

在这里插入图片描述

2. LCR 180. 文件组合

剑指 Offer 57 - II. 和为s的连续正数序列
https://leetcode.cn/problems/he-wei-sde-lian-xu-zheng-shu-xu-lie-lcof/description/

LCR 180. 文件组合

待传输文件被切分成多个部分，按照原排列顺序，每部分文件编号均为一个 正整数（至少含有两个文件）。传输要求为：连续文件编号总和为接收方指定数字 target 的所有文件。请返回所有符合该要求的文件传输组合列表。

注意，返回时需遵循以下规则：

每种组合按照文件编号 升序 排列；
不同组合按照第一个文件编号 升序 排列。

示例 1：

输入：target = 12
输出：[[3, 4, 5]]
解释：在上述示例中，存在一个连续正整数序列的和为 12，为 [3, 4, 5]。

示例 2：

输入：target = 18
输出：[[3,4,5,6],[5,6,7]]
解释：在上述示例中，存在两个连续正整数序列的和分别为 18，分别为 [3, 4, 5, 6] 和 [5, 6, 7]。

提示：

1 <= target <= 10^5

Solution

think about the Enumeration Algorithm
start with the example: from input to output, write it down in ipad

在这里插入图片描述

java

class Solution {
    public int[][] fileCombination(int target) {

        List<int[]> res = new ArrayList<>();

        for (int i = 1; i <= target / 2; i++) {
            int curSum = 0;
            for (int j = i; j < target; j++) {
                curSum += j;
                if (curSum > target) {
                    break;
                }
                if (curSum == target) {
                    int[] combination = new int[j - i + 1];
                    for (int k = i; k <= j; k++) {
                        combination[k - i] = k;
                    }
                    res.add(combination);
                    break;
                }
            }
        }
        return res.toArray(new int[res.size()][]);
    }
}

在这里插入图片描述

Datawhale

1.Enumeration Algorithm

class Solution:
    def findContinuousSequence(self, target: int) -> List[List[int]]:
        res = []
        for i in range(1, target // 2 + 1):
            cur_sum = 0
            for j in range(i, target):
                cur_sum += j
                if cur_sum > target:
                    break
                if cur_sum == target:
                    cur_res = []
                    for k in range(i, j + 1):
                        cur_res.append(k)
                    res.append(cur_res)
                    break
        return res

2.sliding window

class Solution:
    def findContinuousSequence(self, target: int) -> List[List[int]]:
        left, right = 1, 2
        res = []
        while left < right:
            sum = (left + right) * (right - left + 1) // 2
            if sum == target:
                arr = []
                for i in range(0, right - left + 1):
                    arr.append(i + left)
                res.append(arr)
                left += 1
            elif sum < target:
                right += 1
            else:
                left += 1
        return res

Improve：what is sliding window

1.概念
解决数组或字符串中与子数组或子序列相关的问题

可变大小的窗口在数据结构上滑动，以高效地解决问题

2.适合场景
需要在数组或字符串中找到满足特定条件的子数组或子序列。
问题涉及连续的元素。
通过窗口的移动可以减少不必要的计算，提升算法效率。

3.两种常见类型

固定大小的滑动窗口：
通常用于计算一个数组或字符串的连续子数组或子串的最大/最小/总和等。

示例问题：给定一个整数数组 arr 和一个整数 k，找到所有长度为 k 的子数组的最大和。

public int maxSumSubArray(int[] arr, int k) {
    int n = arr.length;
    if (n < k) {
        return -1;
    }

    int maxSum = 0;
    int windowSum = 0;
    
    // 计算第一个窗口的和
    for (int i = 0; i < k; i++) {
        windowSum += arr[i];
    }

    maxSum = windowSum;

    // 滑动窗口：窗口右移，每次增加一个元素，减少一个元素
    for (int i = k; i < n; i++) {
        windowSum += arr[i] - arr[i - k];
        maxSum = Math.max(maxSum, windowSum);
    }

    return maxSum;
}

在这里插入图片描述
可变大小的滑动窗口
窗口的大小不固定，通常用于找到符合某种条件的最小或最大子数组。
窗口会根据情况动态调整大小。
示例问题：给定一个正整数数组 arr 和一个整数 s，找到最短的子数组，使得该子数组的和大于或等于 s。

实现示例：

public int minSubArrayLen(int s, int[] arr) {
    int n = arr.length;
    int left = 0;
    int sum = 0;
    int minLength = Integer.MAX_VALUE;

    for (int right = 0; right < n; right++) {
        sum += arr[right];

        // 当窗口内的和大于等于目标值时，缩小窗口
        while (sum >= s) {
            minLength = Math.min(minLength, right - left + 1);
            sum -= arr[left];
            left++;
        }
    }

    return minLength == Integer.MAX_VALUE ? 0 : minLength;
}

在这里插入图片描述

滑动窗口常见的应用场景
1.字符串问题：查找字符串中满足某些条件的最小或最大子串。例如，查找没有重复字符的最长子串。
2.子数组问题：查找数组中和为某个值的子数组，或者找到和大于某个值的最小子数组。
3.双指针问题：滑动窗口与双指针密切相关，通常也可以认为它是双指针技巧的一种形式

Improve Java

初始化窗口，令 left = 1，right = 2。
计算 sum = (left + right) * (right - left + 1) // 2。
如果 sum == target，时，将其加入答案数组中。
如果 sum < target 时，说明需要扩大窗口，则 right += 1。
如果 sum > target 时，说明需要缩小窗口，则 left += 1。
直到 left >= right 时停止，返回答案数组。

class Solution {
    public int[][] fileCombination(int target) {
        int left = 1;
        int right = 2;
        int sum = left + right;
        List<int[]> res = new ArrayList<>();
        while (left < right) {
            if (sum == target) {
                int[] combination = new int[right - left + 1];
                for (int i = left; i <= right; i++) {
                    combination[i - left] = i;
                }
                res.add(combination);
            }

            if (sum < target) {
                right++;
                sum += right;
            }else{
                sum -= left;
                left++;
            }
        }
        return res.toArray(new int[res.size()][]);
    }
}

在这里插入图片描述

3.2249. Count Lattice Points Inside a Circle 统计圆内格点数目

Given a 2D integer array circles where circles[i] = [xi, yi, ri] represents the center (xi, yi) and radius ri of the ith circle drawn on a grid, return the number of lattice points that are present inside at least one circle.

Note:
A lattice point is a point with integer coordinates.
Points that lie on the circumference of a circle are also considered to be inside it.

Example 1:
在这里插入图片描述

Input: circles = [[2,2,1]]
Output: 5
Explanation:
The figure above shows the given circle.
The lattice points present inside the circle are (1, 2), (2, 1), (2, 2), (2, 3), and (3, 2) and are shown in green.
Other points such as (1, 1) and (1, 3), which are shown in red, are not considered inside the circle.
Hence, the number of lattice points present inside at least one circle is 5.

Example 2:
在这里插入图片描述

Input: circles = [[2,2,2],[3,4,1]]
Output: 16
Explanation:
The figure above shows the given circles.
There are exactly 16 lattice points which are present inside at least one circle.
Some of them are (0, 2), (2, 0), (2, 4), (3, 2), and (4, 4).

Constraints:

1 <= circles.length <= 200
circles[i].length == 3
1 <= xi, yi <= 100
1 <= ri <= min(xi, yi)

Solution

find the rectangle of all circle
using enumeration algorithm to calculate all distance

class Solution {
    public int countLatticePoints(int[][] circles) {
        int min_x = Integer.MAX_VALUE;
        int min_y = Integer.MAX_VALUE;
        int max_x = Integer.MIN_VALUE;
        int max_y = Integer.MIN_VALUE;
        
        // 确定所有圆的边界矩形
        for (int[] circle : circles) {
            int xi = circle[0], yi = circle[1], ri = circle[2];
            min_x = Math.min(min_x, xi - ri);
            max_x = Math.max(max_x, xi + ri);
            min_y = Math.min(min_y, yi - ri);
            max_y = Math.max(max_y, yi + ri);
        }
        
        int ans = 0;
        // 遍历边界矩形内的所有整点
        for (int x = min_x; x <= max_x; x++) {
            for (int y = min_y; y <= max_y; y++) {
                for (int[] circle : circles) {
                    int xi = circle[0], yi = circle[1], ri = circle[2];
                    int dx = xi - x;
                    int dy = yi - y;
                    // 判断点 (x, y) 是否在圆内
                    if (dx * dx + dy * dy <= ri * ri) {
                        ans++;
                        break;
                    }
                }
            }
        }
        
        return ans;
    }
}

在这里插入图片描述

datawhale

class Solution:
    def countLatticePoints(self, circles: List[List[int]]) -> int:
        min_x, min_y = 200, 200
        max_x, max_y = 0, 0
        for circle in circles:
            if circle[0] + circle[2] > max_x:
                max_x = circle[0] + circle[2]
            if circle[0] - circle[2] < min_x:
                min_x = circle[0] - circle[2]
            if circle[1] + circle[2] > max_y:
                max_y = circle[1] + circle[2]
            if circle[1] - circle[2] < min_y:
                min_y = circle[1] - circle[2]
        
        ans = 0
        for x in range(min_x, max_x + 1):
            for y in range(min_y, max_y + 1):
                for xi, yi, ri in circles:
                    if (xi - x) * (xi - x) + (yi - y) * (yi - y) <= ri * ri:
                        ans += 1
                        break
        
        return ans

4. 更多枚举算法题目

https://datawhalechina.github.io/leetcode-notes/#/ch04/04.01/04.01.04-Enumeration-Algorithm-List

在这里插入图片描述

0920 - TASK2：递归算法 Recursion

1.Links

https://github.com/datawhalechina/leetcode-notes/blob/main/docs/ch04/04.02/04.02.01-Recursive-Algorithm.md

2.递归简介

将原问题分解为同类的子问题

函数中再次调用函数自身的方式

「递推过程」和「回归过程」

e.g.阶乘

def fact(n):
    if n == 0:
        return 1
    return n * fact(n - 1)

n=6

fact(6)
= 6 * fact(5)
= 6 * (5 * fact(4))
= 6 * (5 * (4 * fact(3)))
= 6 * (5 * (4 * (3 * fact(2))))
= 6 * (5 * (4 * (3 * (2 * fact(1)))))
= 6 * (5 * (4 * (3 * (2 * (1 * fact(0))))))
= 6 * (5 * (4 * (3 * (2 * (1 * 1)))))
= 6 * (5 * (4 * (3 * (2 * 1))))
= 6 * (5 * (4 * (3 * 2)))
= 6 * (5 * (4 * 6))
= 6 * (5 * 24)
= 6 * 120
= 720

2.递归和数学归纳法

递归的数学模型其实就是「数学归纳法」

从「数学归纳法」的角度来解释递归：

1.递归终止条件：数学归纳法第一步中的 n = b ，可以直接得出结果。
2.递推过程：数学归纳法第二步中的假设部分（假设 n = k 时命题成立），也就是假设我们当前已经知道了 n = k 时的计算结果。
3.回归过程：数学归纳法第二步中的推论部分（根据 n = k 推论出 n = k + 1 ），也就是根据下一层的结果，计算出上一层的结果。

事实上，数学归纳法的思考过程也正是在解决某些数列问题时，可以使用递归算法的原因。比如阶乘、数组前 n 项和、斐波那契数列等等。

e.g.
设想计算阶乘 n! 的递归算法。
1.递归的终止条件是 n = 0 时，返回 1。这是阶乘的基础事实：0! = 1。
对应数学归纳法中的基础情况：我们验证当 n = 0 时命题 n! 成立。
假设当 n = k 时，阶乘公式 k! 已经成立。
通过 k! 推导出 k + 1!，从而证明整个命题对于所有 n 成立。

3. 递归三步走

1.写出递推公式：找到将原问题分解为子问题的规律，并且根据规律写出递推公式。
2.明确终止条件：推敲出递归的终止条件，以及递归终止时的处理方法。
3.将递推公式和终止条件翻译成代码：
定义递归函数（明确函数意义、传入参数、返回结果等）。
书写递归主体（提取重复的逻辑，缩小问题规模）。
明确递归终止条件（给出递归终止条件，以及递归终止时的处理方法）。

e.g. calculate n!
formula：（k+1）！=（k+1）* k！
End：0！=1
阶乘函数 fact ( n ) ，这个函数的传入参数是问题的规模 n ，最终返回的结果是 n 的阶乘值

def recursion(大规模问题):
if 递归终止条件:
递归终止时的处理方法
return recursion(小规模问题)

4. 递归的注意点

4.1 避免栈溢出

1.可以在代码中限制递归调用的最大深度来解决问题。当递归调用超过一定深度时（比如 100）之后，不再进行递归，而是直接返回报错。
2.考虑将递归算法变为**非递归算法（即递推算法）**来解决栈溢出的问题。

4.2 避免重复运算

斐波那契数列
在这里插入图片描述使用一个缓存（哈希表、集合或数组）来保存已经求解过的 f ( k ) 的结果，这也是动态规划算法中的做法

5. 递归的应用

6.斐波那契数 509. Fibonacci Number

The Fibonacci numbers, commonly denoted F(n) form a sequence, called the Fibonacci sequence, such that each number is the sum of the two preceding ones, starting from 0 and 1. That is,

F(0) = 0, F(1) = 1
F(n) = F(n - 1) + F(n - 2), for n > 1.

Given n, calculate F(n).

Example 1:
Input: n = 2
Output: 1
Explanation: F(2) = F(1) + F(0) = 1 + 0 = 1.

Example 2:

Input: n = 3
Output: 2
Explanation: F(3) = F(2) + F(1) = 1 + 1 = 2.

Example 3:

Input: n = 4
Output: 3
Explanation: F(4) = F(3) + F(2) = 2 + 1 = 3.

Constraints:
0 <= n <= 30

Solution

1.find the formula
F(n) = F(n - 1) + F(n - 2), for n > 1.
2.find the end condition
F(0) = 0, F(1) = 1
3.definite the input output and end condition

java-version1

class Solution {
    
    public int fib(int n) {
        if(n < 0){
            return -1;
        }else if(n == 0){
            return 0;
        }else if(n == 1){
            return 1;
        }
        return fib(n-1)+fib(n-2);
    }
}

在这里插入图片描述

java-version2-avoid recalculate problem: no Recursion

class Solution {

    public int fib(int n) {
        if (n == 0) {
            return 0;
        } else if (n == 1) {
            return 1;
        } else {
            int a = 0; // F(0)
            int b = 1; // F(1)
            int c = 0;
            for (int i = 2; i <= n; i++) {
                c = a + b; // Next Fibonacci number
                a = b;
                b = c;
            }
            return b;
        }
    }
}

在这里插入图片描述

java-version2.2-avoid recalculate problem: store Fibonacci number

class Solution {
    public int fib(int n) {
        if (n <= 1) {
            return n;
        }

        int[] dp = new int[n + 1]; // Array to store Fibonacci numbers
        dp[0] = 0;
        dp[1] = 1;

        for (int i = 2; i <= n; i++) {
            dp[i] = dp[i - 2] + dp[i - 1];
        }

        return dp[n];
    }
}

在这里插入图片描述

DATAWHALE

class Solution:
    def fib(self, n: int) -> int:
        if n == 0:
            return 0
        if n == 1:
            return 1
        return self.fib(n - 1) + self.fib(n - 2)

class Solution:
    def fib(self, n: int) -> int:
        if n <= 1:
            return n

        dp = [0 for _ in range(n + 1)]
        dp[0] = 0
        dp[1] = 1
        for i in range(2, n + 1):
            dp[i] = dp[i - 2] + dp[i - 1]

        return dp[n]

7.二叉树的最大深度 104. Maximum Depth of Binary Tree

https://leetcode.cn/problems/maximum-depth-of-binary-tree/description/

Given the root of a binary tree, return its maximum depth.

A binary tree’s maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Example 1:
在这里插入图片描述

Input: root = [3,9,20,null,null,15,7]
Output: 3

Example 2:

Input: root = [1,null,2]
Output: 2

Constraints:
The number of nodes in the tree is in the range [0, 104].
-100 <= Node.val <= 100

Solution

在这里插入图片描述

Java-version1

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 * int val;
 * TreeNode left;
 * TreeNode right;
 * TreeNode() {}
 * TreeNode(int val) { this.val = val; }
 * TreeNode(int val, TreeNode left, TreeNode right) {
 * this.val = val;
 * this.left = left;
 * this.right = right;
 * }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null){
            return 0;
        }
        if (root.left == null && root.right == null) {
            return 1;
        } else if (root.left != null && root.right != null) {
            return Math.max(maxDepth(root.left) + 1, maxDepth(root.right) + 1);
        } else if (root.left != null && root.right == null) {
            return Math.max(maxDepth(root.left) + 1, 1);
        } else {
            return Math.max(1, maxDepth(root.right) + 1);
        }
    }
}

在这里插入图片描述

Datawhale

class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0
        
        return max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1

java-version2:

改进，不用判断null，如果为空，直接返回0，不会影响算法

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 * int val;
 * TreeNode left;
 * TreeNode right;
 * TreeNode() {}
 * TreeNode(int val) { this.val = val; }
 * TreeNode(int val, TreeNode left, TreeNode right) {
 * this.val = val;
 * this.left = left;
 * this.right = right;
 * }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null){
            return 0;
        }
        //改进，不用判断null，如果为空，直接返回0，不会影响算法
        return Math.max(maxDepth(root.left), maxDepth(root.right))+1;
    }
}

在这里插入图片描述

0921- TASK2-Exercises

1.Links

目录
https://github.com/datawhalechina/leetcode-notes/blob/main/docs/ch04/index.md
题目
https://datawhalechina.github.io/leetcode-notes/#/ch04/04.02/04.02.02-Exercises

2.爬楼梯 70. Climbing Stairs

You are climbing a staircase. It takes n steps to reach the top.

Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

Example 1:
Input: n = 2
Output: 2
Explanation: There are two ways to climb to the top.

1 step + 1 step
2 steps

Example 2:
Input: n = 3
Output: 3
Explanation: There are three ways to climb to the top.

1 step + 1 step + 1 step
1 step + 2 steps
2 steps + 1 step

Constraints:
1 <= n <= 45

Solution

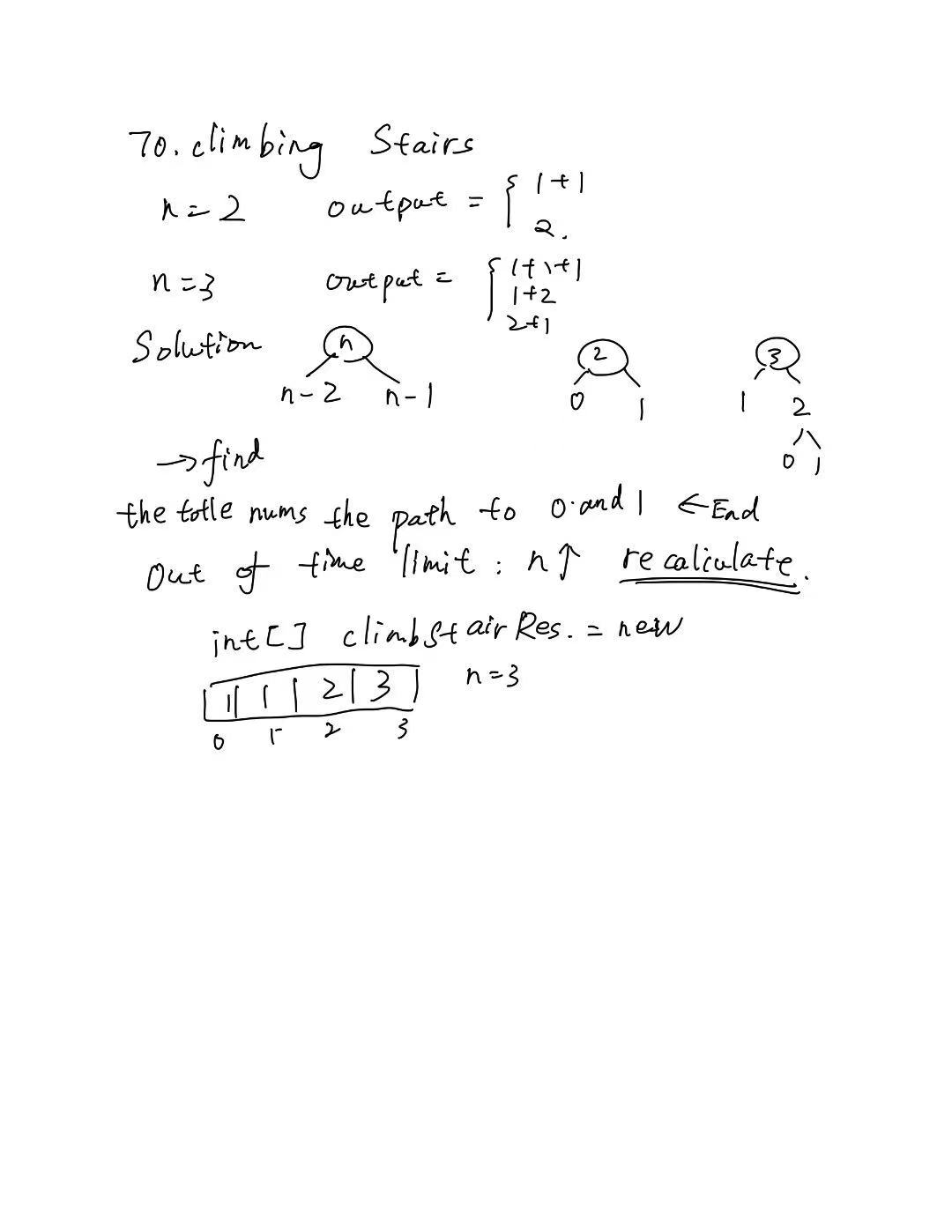
在这里插入图片描述

Java-version1

超出时间限制：需要存储之前计算后的结果，来改进

class Solution {
    public int climbStairs(int n) {
        if(n==1 || n==0){
            return 1;
        }
        return climbStairs(n-2) + climbStairs(n-1);
    }
}

Java-version2

class Solution {
    public int climbStairs(int n) {
        if(n==1 || n==0){
            return 1;
        }
        
        int[] climbingStairsResult = new int[n+1];
        climbingStairsResult[0] = 1;
        climbingStairsResult[1] = 1;

        for (int i = 2; i <= n; i++) {
            climbingStairsResult[i] = climbingStairsResult[i - 2] + climbingStairsResult[i - 1];
        }

        return climbingStairsResult[n];
    }
}

在这里插入图片描述

Datawhale

https://github.com/datawhalechina/leetcode-notes/blob/main/docs/solutions/0070.md

class Solution:
    def climbStairs(self, n: int) -> int:
        if n == 1:
            return 1
        if n == 2:
            return 2
        return self.climbStairs(n - 1) + self.climbStairs(n - 2)

class Solution:
    def climbStairs(self, n: int) -> int:
        dp = [0 for _ in range(n + 1)]
        dp[0] = 1
        dp[1] = 1
        for i in range(2, n + 1):
            dp[i] = dp[i - 1] + dp[i - 2]
        
        return dp[n]

3.翻转二叉树 226. Invert Binary Tree

https://leetcode.cn/problems/invert-binary-tree/description/

Given the root of a binary tree, invert the tree, and return its root.

Example 1:
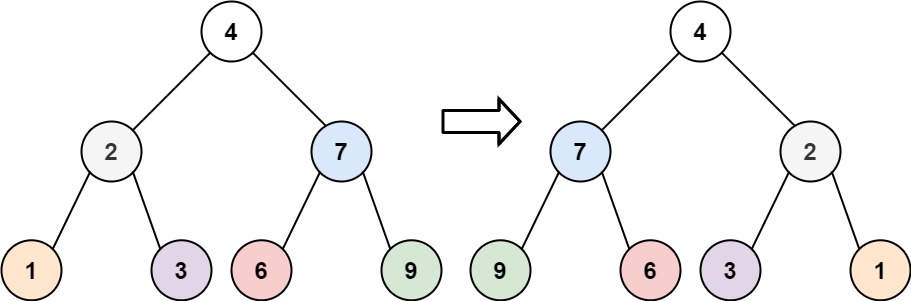
在这里插入图片描述

Input: root = [4,2,7,1,3,6,9]
Output: [4,7,2,9,6,3,1]

Example 2:
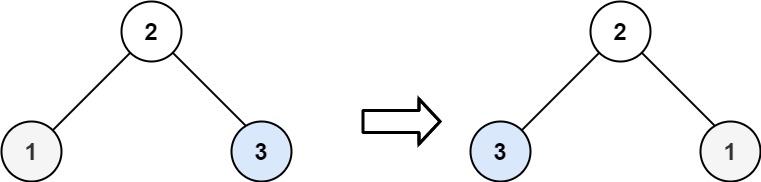
在这里插入图片描述

Input: root = [2,1,3]
Output: [2,3,1]

Example 3:

Input: root = []
Output: []

Constraints:

The number of nodes in the tree is in the range [0, 100].
-100 <= Node.val <= 100

Solution

Java-version1

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null){
            return null;
        }

        TreeNode left = invertTree(root.left);
        TreeNode right = invertTree(root.right);
        

        root.left = right;
        root.right = left;
        
        return root;
    }
}

在这里插入图片描述

Datawhale

https://github.com/datawhalechina/leetcode-notes/blob/main/docs/solutions/0226.md

class Solution:
    def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        if not root:
            return None
        left = self.invertTree(root.left)
        right = self.invertTree(root.right)
        root.left = right
        root.right = left
        return root

0924-Task3 - 回溯算法 Backtracking

1.Links

1.目录
https://github.com/datawhalechina/leetcode-notes/blob/main/docs/ch04/index.md
2.回溯算法介绍
https://github.com/datawhalechina/leetcode-notes/blob/main/docs/ch04/04.03/04.03.01-Backtracking-Algorithm.md

2.回溯算法

2.1回溯算法（Backtracking）介绍

回溯算法（Backtracking）：一种能避免不必要搜索的穷举式的搜索算法。采用试错的思想，在搜索尝试过程中寻找问题的解，当探索到某一步时，发现原先的选择并不满足求解条件，或者还需要满足更多求解条件时，就退回一步（回溯）重新选择，这种走不通就退回再走的技术称为「回溯法」，而满足回溯条件的某个状态的点称为「回溯点」。

简单来说，回溯算法采用了一种「走不通就回退」的算法思想。

回溯算法通常用简单的递归方法来实现，在进行回溯过程中更可能会出现两种情况：

找到一个可能存在的正确答案；
在尝试了所有可能的分布方法之后宣布该问题没有答案。

2.2 从全排列问题开始理解回溯算法

在这里插入图片描述

Example：回溯法生成一个整数列表的所有排列

通过递归构建排列并使用撤销操作来探索所有可能的排列。
每当发现一个完整的排列时，就将其加入结果集中。

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        res = []    # 存放所有符合条件结果的集合
        path = []   # 存放当前符合条件的结果
        def backtracking(nums):             # nums 为选择元素列表
            if len(path) == len(nums):      # 说明找到了一组符合条件的结果
                res.append(path[:])         # 将当前符合条件的结果放入集合中
                return

            for i in range(len(nums)):      # 枚举可选元素列表
                if nums[i] not in path:     # 从当前路径中没有出现的数字中选择
                    path.append(nums[i])    # 选择元素
                    backtracking(nums)      # 递归搜索
                    path.pop()              # 撤销选择

        backtracking(nums)
        return res

举个例子：

假设 nums = [1, 2, 3]，执行过程如下：
初始状态：

res = []
path = []
nums = [1, 2, 3]

第一次递归：

选择 1，path = [1]。
递归进入下一层，选择 2，path = [1, 2]。
递归进入下一层，选择 3，path = [1, 2, 3]，此时 path 长度与 nums 长度相同，将其加入 res，即 res = [[1, 2, 3]]。
撤销选择，path = [1, 2]，返回上一步，尝试其他选择。

第二次递归：

从 path = [1, 2] 状态下撤销 2，返回 path = [1]。
选择 3，path = [1, 3]。
递归进入下一层，选择 2，path = [1, 3, 2]，此时 path 长度与 nums 长度相同，将其加入 res，即 res = [[1, 2, 3], [1, 3, 2]]。
撤销选择，path = [1, 3]，再撤销选择 3，回到 path = [1]。

重复这个过程，继续进行递归，直到所有可能的排列都被找到。最终，res 将包含所有排列结果，即：
[[1, 2, 3],
[1, 3, 2],
[2, 1, 3],
[2, 3, 1],
[3, 1, 2],
[3, 2, 1]]

2.3. 回溯算法的通用模板

res = []    # 存放所欲符合条件结果的集合
path = []   # 存放当前符合条件的结果
def backtracking(nums):             # nums 为选择元素列表
    if 遇到边界条件:                  # 说明找到了一组符合条件的结果
        res.append(path[:])         # 将当前符合条件的结果放入集合中
        return

    for i in range(len(nums)):      # 枚举可选元素列表
        path.append(nums[i])        # 选择元素
        backtracking(nums)          # 递归搜索
        path.pop()                  # 撤销选择

backtracking(nums)

2.4. 回溯算法三步走

以深度优先搜索的方式，根据产生子节点的条件约束，搜索问题的解。当发现当前节点已不满足求解条件时，就「回溯」返回，尝试其他的路径。

1.明确所有选择：画出搜索过程的决策树，根据决策树来确定搜索路径。
2.明确终止条件：推敲出递归的终止条件，以及递归终止时的要执行的处理方法。
3.将决策树和终止条件翻译成代码：
定义回溯函数（明确函数意义、传入参数、返回结果等）。
书写回溯函数主体（给出约束条件、选择元素、递归搜索、撤销选择部分）。
明确递归终止条件（给出递归终止条件，以及递归终止时的处理方法）。

3.回溯算法的应用

子集
N 皇后

4.子集 78. Subsets

https://leetcode.cn/problems/subsets/description/

Given an integer array nums of unique elements, return all possible
subsets
(the power set).

The solution set must not contain duplicate subsets. Return the solution in any order.

Example 1:

Input: nums = [1,2,3]
Output: [[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

Example 2:

Input: nums = [0]
Output: [[],[0]]

Constraints:

1 <= nums.length <= 10
-10 <= nums[i] <= 10
All the numbers of nums are unique.

Solution

假设 nums = [1, 2, 3]，递归的流程如下：

开始时 t = []，表示空集。
选择 1，此时 t = [1]。
    选择 2，此时 t = [1, 2]。
        选择 3，此时 t = [1, 2, 3]，达到末尾，保存 [1, 2, 3]。
        回溯，移除 3，此时 t = [1, 2]，保存 [1, 2]。
    回溯，移除 2，此时 t = [1]。
        选择 3，此时 t = [1, 3]，保存 [1, 3]。
    回溯，移除 3，此时 t = [1]，保存 [1]。
回溯，移除 1，此时 t = []。
    选择 2，此时 t = [2]。
        选择 3，此时 t = [2, 3]，保存 [2, 3]。
        回溯，移除 3，此时 t = [2]，保存 [2]。
    回溯，移除 2，此时 t = []。
        选择 3，此时 t = [3]，保存 [3]。
    回溯，移除 3，此时 t = []，保存 []。

在 Java 中，当我们将一个对象（例如 List）添加到另一个数据结构（如 ans）时，添加的是对象的引用，而不是对象的副本。也就是说，ans.add(t) 实际上将 t 的引用添加到了 ans 中。如果之后 t 被修改，那么存储在 ans 中的引用指向的对象也会发生变化，导致 ans 中的子集不正确。
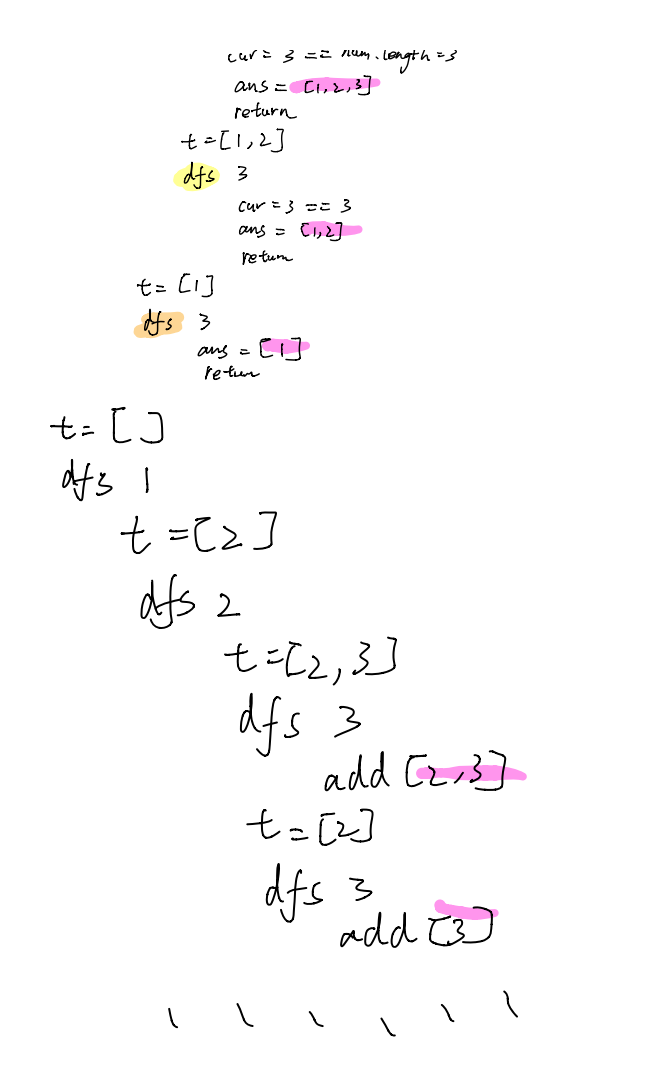
在这里插入图片描述

Java-version1

class Solution {
  
    List<Integer> t = new ArrayList<Integer>();
    //存储所有子集的结果列表
    List<List<Integer>> ans = new ArrayList<List<Integer>>();

    public List<List<Integer>> subsets(int[] nums) {
        //深度优先搜索
        dfs(0, nums);
        return ans;
    }
    //当前递归的数组下标，表示正在处理第 cur 个元素。
    public void dfs(int cur, int[] nums) {
        //当 cur 到达数组的末尾时，表示已经处理完了数组中的所有元素。
        if (cur == nums.length) {
            //此时，将当前构建的子集 t加入到结果列表 ans 中
            //注意，这里需要创建一个新的列表，因为 t 会在后续递归中被修改。
            ans.add(new ArrayList<Integer>(t));
            //结束递归
            return;
        }
        t.add(nums[cur]) ;
        dfs(cur + 1, nums);
        t.remove(t.size() - 1);
        dfs(cur + 1, nums);
    }
}

在这里插入图片描述

1001-优秀学习者-发表感言

各位力扣大佬晚上好，非常荣幸，被选为优秀学习者来给大家分享一下学习经验与想法。今晚我想要分享三点内容。
1.光说不练假把式
Just do it. 最令人遗憾优秀学习者的不是目标没有达成，而是甚至还没来得及追求梦想[1]。从我最近读过的《我在100天内自学
英文翻转人生》[2]中也提到过类似的思想，英语如果不说出口，看美剧不重复跟读，背诵再多的单词，都说不出完整的话。言归正传，代码如果不是自己手动上手敲的话，只看官方题解或者Datawhale题解，永远也学不会代码。题解的意义不是让我们看完，就当这题做过了，而是在自己写完以后，辅助自己寻找自己代码不足，并且向优秀的代码学习，促使自己代码迭代，我想，这些才是题解的意义。
但是有时确实发现自己确实由于相关知识的缺乏，没有相关思路，例如我在回溯算法的时候所遇到的一样，可以参考leetcode和datawhale的官方题解先进行理解，但是不能只停留在理解完就完了，而是要自己关闭题解，自己上手写过，并对照迭代，才能算为掌握了这个题。并且，由于对于算法陌生，应该多练几题，争取打到不看题解，至少能把代码跑过，才能保证自己在秋春招的真实环境，将算法用出来。
2.Example
我们总会在理解算法和解题过程中陷入困顿，不知道如何下手。我们应该从最简单的例子开始，设计自己的程序，保证可以跑过题目要求的最简单的示例，这就是为啥leetcode要设置Example。设计程序时，不仅只是头脑风暴后就开始直接编程（大佬除外，对求解流程十分熟悉除外）。写下来，是理解算法和帮助自己解题的一大利器，他不是要求写出抽象的步骤，而是用过例子，具体的数字，来写出解题例子的流程。这个我也是从书中LS100的step3感悟的[2]。
3.English
程序员应该具备英语素质，leetcode提供英文题目，建立于代码的编写要求对变量进行命名，如果没有合适的英语素养，或者对于题目的英文要求不熟悉。就难以命名出信达雅的名字，所以我推荐阅读英文leetcode，锻炼自己在编程方面英语的阅读能力。如果可以，我推荐英文注释，这样可以保证跨国协作的顺利进行，也可以防止中文注释变乱码。

Reference
[1]【TED经典：今晚DDL的你还在刷b站？【TED演讲】】 https://www.bilibili.com/video/BV1jT411X7Dz/?share_source=copy_web&vd_source=9346d1baa752b5ddda5636787cd547f4
[2]《我在100天内自学英文翻转人生》https://weread.qq.com/web/bookDetail/c4132f0071ed8d4cc418130