【AI深究】层次聚类（Hierarchical Clustering）四大链接法全网最详细全流程详解与案例（附Python代码演示） | 单链法、全链法、平均法、中心法 | 例子案例及数据

大家好，我是爱酱。本期我们将用详细案例和流程，分别演示单链法、全链法、平均法和中心法四种主流链接方式的层次聚类。每种方法都配有具体合并步骤、距离计算和结果解读，帮助新手和进阶读者彻底理解层次聚类的核心思想和实际操作。

注：本文章含大量数学算式、详细例子说明及代码演示，大量干货，建议先收藏再慢慢观看理解。新频道发展不易，你们的每个赞、收藏跟转发都是我继续分享的动力！

---

一、层次聚类的基本流程

我们先要知道聚类的种类：

• 凝聚型（Agglomerative）：每个点单独为一类，逐步合并最近的两类，直到只剩一个大类或达到预设簇数。

• 分裂型（Divisive）：所有点先是一类，逐步分裂成更小的簇，直到每个点单独成类或达到预设簇数。

实际应用中，凝聚型更常用。在这篇文章，我们也会预设使用凝聚型。相信大家在搞明白凝聚型后，也能举一反三，知道分裂型是怎么运作的！

---

二、距离度量与四大链接法

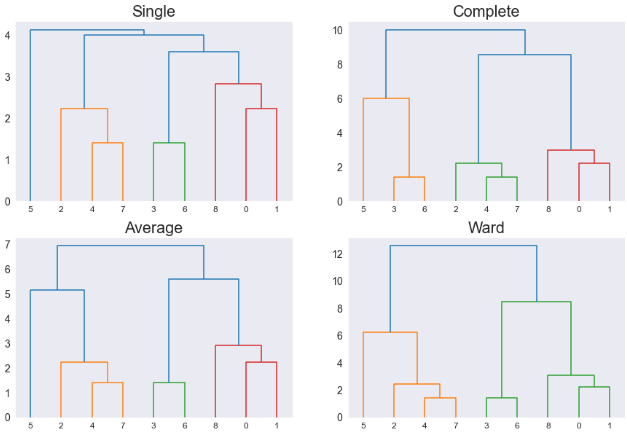
1. 单链法（Single Linkage）

2. 全链法（Complete Linkage）

3. 平均法（Average Linkage）

4. 中心法（Centroid Linkage）

其中 、 分别为簇 和 的均值。

---

三、案例数据

假设有5个样本点：A、B、C、D、E，欧氏距离矩阵（Euclidean Distance Matrix）如下：
基本上，表格的数字就是代表该点于目标点的绝对距离差异（标量）。

	A	B	C	D	E
A	0	2	6	10	9
B	2	0	5	9	8
C	6	5	0	4	5
D	10	9	4	0	3
E	9	8	5	3	0

---

四、四大链接法的完整流程

1. 单链法（Single Linkage）流程

Step 1：初始化

每个点为一类：