LC785.判断二分图(BFS/DFS/并查集)

LC785.判断二分图

785. 判断二分图

难度中等329

存在一个 无向图 ，图中有 n 个节点。其中每个节点都有一个介于 0 到 n - 1 之间的唯一编号。给你一个二维数组 graph ，其中 graph[u] 是一个节点数组，由节点 u 的邻接节点组成。形式上，对于 graph[u] 中的每个 v ，都存在一条位于节点 u 和节点 v 之间的无向边。该无向图同时具有以下属性：

• 不存在自环（graph[u] 不包含 u）。
• 不存在平行边（graph[u] 不包含重复值）。
• 如果 v 在 graph[u] 内，那么 u 也应该在 graph[v] 内（该图是无向图）
• 这个图可能不是连通图，也就是说两个节点 u 和 v 之间可能不存在一条连通彼此的路径。

二分图 定义：如果能将一个图的节点集合分割成两个独立的子集 A 和 B ，并使图中的每一条边的两个节点一个来自 A 集合，一个来自 B 集合，就将这个图称为 二分图 。

如果图是二分图，返回 true ；否则，返回 false 。

示例 1：

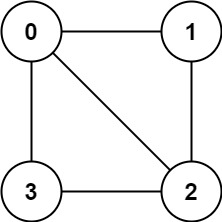
输入：graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
输出：false
解释：不能将节点分割成两个独立的子集，以使每条边都连通一个子集中的一个节点与另一个子集中的一个节点。

示例 2：

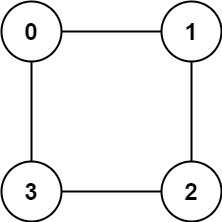
输入：graph = [[1,3],[0,2],[1,3],[0,2]]
输出：true
解释：可以将节点分成两组: {0, 2} 和 {1, 3} 。

分析

首先，无论什么题目拿到手里面第一步都是把题目的意思弄清楚。

题目要求我们判断一个无向图是否为一个二分图

什么是二分图，就是在一条边两侧的节点属于不同的集合

这时候能想到的方法是

搜索

将一个节点的周边节点归为一个集合，如果遇到重复的集合，那么就说明不是二分图

并查集

也就是将与一个节点相连的其他节点归并起来成为一个集合，如果当前节点在集合内就不是二值图。

题解

BFS

class Solution {
public:

    bool isBipartite(vector<vector<int>>& graph) {

        return BFS(graph);
    }

    /* 
        如果是二分图，那么有
        能够对所有的点进行访问染色
        每一条边上的两个顶点颜色不一样

        二分图： 其实就是每一个连通区域里面的节点颜色两两相邻不一样的图
     */
    bool BFS(vector<vector<int>>& graph) {
        // 表示访问过的点
        vector<int> visited(graph.size());
        // 开始搜索每一个连通区域
        queue<int> que;
        for(int i=0;i<graph.size();i++) { // 开始搜索每一个连通区域
            if(visited[i]!=0) {
                continue;
            }

            que.push(i);
            visited[i]=1;
            // 开始进行染色
            while(!que.empty()) {
                int size = que.size();
                for(int k=0;k<size;k++) {
                    int val = que.front();
                    que.pop();
                    // 将两边染色
                    for(auto v : graph[val]) {
                        if(visited[v]==visited[val]) {
                            return false;
                        } else if(visited[v]==0) { // 没访问过的才染色
                            visited[v]=-visited[val];
                            que.push(v);
                        }

                    }
                }
            }

        }
        return true;
        

    }

};

DFS

class Solution {
public:
    bool isBipartite(vector<vector<int>>& graph) {

        return DFS(graph);
    }

    bool DFS(vector<vector<int>>& graph) {
        vector<int> visited(graph.size(),0);
        for(int i=0;i<graph.size();i++) {
            if(visited[i]!=0) {
                continue;
            }
            // 开始染色
            if(!dfs(graph,visited,i,1)){
                return false;
            }
        }
        return true;

    }
   // now_color表示当前需要染的颜色，用1代表集合A -1代表集合B
    bool dfs(vector<vector<int>>& graph, vector<int>& visited, int index, int now_color) { // 访问时候直接染色
            if(visited[index]!=0) { // 如果访问过
                return visited[index]==now_color;  // 当前颜色与需要颜色不一致就返回false
            }

            visited[index]=now_color; // 染色
            bool ans = true;
            for(auto v : graph[index]) {
                ans = ans & dfs(graph,visited,v,-now_color);
            }
            return ans;

    }


};

并查集

class UFind {
    public:

    UFind(int size) {
        weight_.resize(size,1);
        father_.resize(size,-1);  // 一开始爸爸都是自己
        for(int i=0;i<father_.size();i++) {
            father_[i]=i;
        }
    }


    // 开始Find
    int Find(int x) { // 找到x的带头大哥
        while(father_[x]!=x) {
            
            father_[x]=father_[father_[x]];
            x=father_[x];
        }
        return x;
    }

    void Union(int x, int y) {
        int father_x = Find(x);
        int father_y = Find(y);
        if(father_x==father_y) {
            return;
        }

        if(weight_[father_x]>weight_[father_y]) {
            father_[father_y]=father_x;
            weight_[father_x]+=weight_[father_y];
        } else {
            father_[father_x]=father_y;
            weight_[father_y]+=weight_[father_x];
        }
    }



    private:
    vector<int> weight_;
    vector<int> father_;
};

class Solution {
public:
    
    /* 
        也可以用并查集去解决
        也就是，一条边中对立的顶点在一个集合，且自身不在这个集合之内
    
     */

    bool isBipartite(vector<vector<int>>& graph) {
        // 生成一个并查集
        UFind u(graph.size());
        for(int i=0;i<graph.size();i++) {
            if(graph[i].size()>1) {
                for(int j=1;j<graph[i].size();j++) {
                    u.Union(graph[i][j-1],graph[i][j]);
                }
            }
            // 自己不在这个集合中
            if(graph[i].size()>0) {
                if(u.Find(i)==u.Find(graph[i][0])) {
                    return false;
                }
            }
        }
        return true;

    }
};