1609. 奇偶树(广度优先搜索)

最新推荐文章于 2025-12-26 09:17:23 发布

原创最新推荐文章于 2025-12-26 09:17:23 发布 · 150 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #leetcode

leetcode刷题之旅专栏收录该内容

39 篇文章

订阅专栏

该博客讨论了一种特殊的二叉树——奇偶树，其中偶数层级的节点值是奇数且递增，奇数层级的节点值是偶数且递减。文章提供了一个C++解决方案，通过广度优先搜索遍历树的每一层，验证每层节点值是否符合奇偶树的条件。在每个遍历层级中，分别检查偶数层和奇数层的节点值是否满足递增或递减且奇偶性正确，从而判断树是否为奇偶树。

1609. 奇偶树

难度中等44

如果一棵二叉树满足下述几个条件，则可以称为 奇偶树 ：

二叉树根节点所在层下标为 0 ，根的子节点所在层下标为 1 ，根的孙节点所在层下标为 2 ，依此类推。
偶数下标 层上的所有节点的值都是奇整数，从左到右按顺序 严格递增
奇数下标 层上的所有节点的值都是偶整数，从左到右按顺序 严格递减

给你二叉树的根节点，如果二叉树为 奇偶树 ，则返回 true ，否则返回 false 。

示例 1：

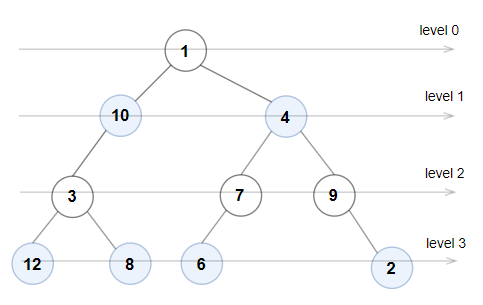
输入：root = [1,10,4,3,null,7,9,12,8,6,null,null,2]
输出：true
解释：每一层的节点值分别是：
0 层：[1]
1 层：[10,4]
2 层：[3,7,9]
3 层：[12,8,6,2]
由于 0 层和 2 层上的节点值都是奇数且严格递增，而 1 层和 3 层上的节点值都是偶数且严格递减，因此这是一棵奇偶树。

示例 2：

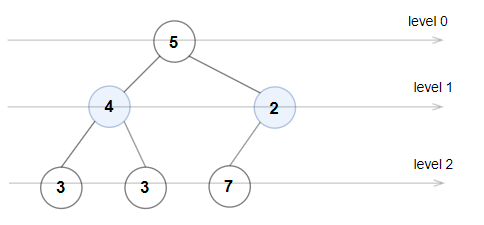
输入：root = [5,4,2,3,3,7]
输出：false
解释：每一层的节点值分别是：
0 层：[5]
1 层：[4,2]
2 层：[3,3,7]
2 层上的节点值不满足严格递增的条件，所以这不是一棵奇偶树。

示例 3：

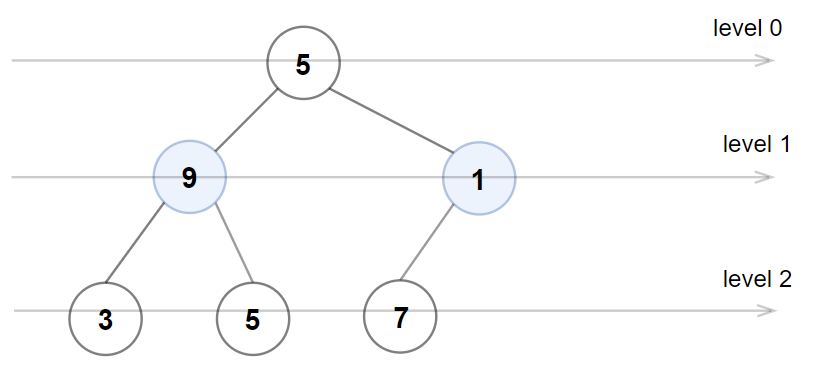
输入：root = [5,9,1,3,5,7]
输出：false
解释：1 层上的节点值应为偶数。

示例 4：

输入：root = [1]
输出：true

示例 5：

输入：root = [11,8,6,1,3,9,11,30,20,18,16,12,10,4,2,17]
输出：true

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

/* 
    其实就是验证每一行的数据

 */

class Solution {
public:
    bool isEvenOddTree(TreeNode* root) {
        // 开始遍历
        int cen = 0;
        if(root==nullptr) {
            return false;
        }
        queue<TreeNode* > que;
        que.push(root);
        while(!que.empty()) {
            int size = que.size();
            vector<int> ve;

            for(int i=0;i<size;i++) {
                auto p = que.front();
                que.pop();
                ve.push_back(p->val);
                if(p->left) {
                    que.push(p->left);
                }
                
                if(p->right) {
                    que.push(p->right);
                }
            }
            if(cen%2==0) {
                if(!Ji(ve)) {
                    return false;
                }
            } else {
                if(!Ou(ve)) {
                    return false;
                }
            }
            cen++;

        }
        return true;
        

    }

    bool Ji(vector<int>& data) {
        // 满足都是奇数而且严格递增
        if(data.empty()) {
            return false;
        }
        if(data[0]%2==0) {
            return false;
        }

        for(int i=1;i<data.size();i++) {
            if(data[i]-data[i-1]<=0 || data[i]%2==0) {
                return false;
            }
        }
        return true;

    }


    bool Ou(vector<int>& data) {
        // 满足都是奇数而且严格递增
        if(data.empty()) {
            return false;
        }
        if(data[0]%2!=0) {
            return false;
        }

        for(int i=1;i<data.size();i++) {
            if(data[i]-data[i-1]>=0 || data[i]%2!=0) {
                return false;
            }
        }
        return true;

    }

};