leetcode之递归详解

递归

其实递归和二叉树遍历很像,要理解递归,就要理解二叉树遍历.

可以看看这个理解一下

首先说明一个问题，简单阐述一下递归，分治算法，动态规划，贪心算法这几个东西的区别和联系，心里有个印象就好。

递归这种尽量能不用就不用,有时候会造成过大的额外开销以及栈溢出,可以根据这个思想选用贪心算法,动态规划,bfs,dfs等

递归是一种编程技巧，一种解决问题的思维方式；分治算法和动态规划很大程度上是递归思想基础上的（虽然动态规划的最终版本大都不是递归了，但解题思想离不开递归），解决更具体问题的两类算法思想；贪心算法是动态规划算法的一个子集，可以更高效解决一部分更特殊的问题。以最经典的归并排序为例，它把待排序数组不断二分为规模更小的子问题处理，这就是 “分而治之” 这个词的由来。显然，排序问题分解出的子问题是不重复的，如果有的问题分解后的子问题有重复的（重叠子问题性质），那么就交给动态规划算法去解决！

使用递归的关键是要明白：递归函数的作用是什么，从宏观的角度去理解递归，不用太在意递归是如何进行调用的。
如果想具体的进一步了解，可以使用小的数据量进行手动的推导，深度的理解递归中的具体调用。

递归有两个重要的组成部分：

递归终止条件： 用来跳出递归，写好递归先从简单的入手，弄清楚最简单的情况，就可以写出终止条件
具体实现：实现递归函数的功能

明白一个函数的作用并相信它能完成这个任务，千万不要试图跳进细节

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

    3
   / \
  9  20
    /  \
   15   7

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int recall(TreeNode* root,int depth)
    {
        if(root==NULL)
        return depth;
        int a=recall(root->left,depth+1);//左边子树的最大深度
        int b=recall(root->right,depth+1);//右边子树的最大深度
        return max(a,b);
    }
    int maxDepth(TreeNode* root) {
        int depth=0;//这里为什么初始值是0呢?
        return recall(root,depth);//确定这个函数的作用就是给定root返回左右子树的最大深度;
        
    }
};
/* 为什么初始值为0 因为为NULL的终止条件相当于加了1正好是root第一层 */

---

递归递归先递后归

比如阶乘

f(6)=> 6 * f(5)=> 6 * (5 * f(4))=> 6 * (5 * (4 * f(3)))=> 6 * (5 * (4 * (3 * f(2))))=> 6 * (5 * (4 * (3 * (2 * f(1)))))=> 6 * (5 * (4 * (3 * (2 * 1))))=> 6 * (5 * (4 * (3 * 2)))=> 6 * (5 * (4 * 6))=> 6 * (5 * 24)=> 6 * 120=> 720

先进去然后再逐层返回

重点来了

递归的套路

套路一：不要纠结递归的整个过程。

既然递归是一个反复调用自身的过程，这就说明它每一级的功能都是一样的，因此我们只需要关注一级递归的解决过程即可。

套路二：这个主函数是做什么的。

套路三：找到整个递归的终止条件,也就是说终止条件是什么,在满足终止条件情况下里面又做了什么。

套路四：找返回值：应该给上一级返回什么信息。

套路五：我们精简后的一级递归是用来做什么的。

总之就是:这个问题怎么分成子问题,这个函数干了什么,进去前干啥,出来后干啥,以及我要返回上一层内容是啥;
相信各位可以发现这个和动态规划很像,有[备忘录]的递归效率就差不多和动态规划一样;不一样的思路.动态规划的自底向上.

(1)判断是否有最优子结构(没有就转化)

(2)确定状态变量

(3)确定dp数组含义以及大小

(4)选择择优,数学归纳找出转移方程

(4)找到base case

(5)选择遍历dp方向

(6)看看能不能优化,也就是状态压缩

可以看出,递归是由目标点一直到终止条件再逐层返回,而动态规划是由终止条件一直迭代到目标点

eg.

给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。

说明: 叶子节点是指没有子节点的节点。

给定如下二叉树，以及目标和 sum = 22，

          5
         / \
        4   8
       /   / \
      11  13  4
     /  \      \
    7    2      1

思路: 函数:给定节点,判定是否达到目标

终止条件:子节点,判定是否符合结果

下一层是一左一右节点有没有满足;返回上一层的结果只要有一个为true就可以;

所以列出函数

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool a(TreeNode* root,int target,int sum)
    {
         if(root==NULL) return false;
        target+=root->val;
        if(root->left==NULL&&root->right==NULL&&target==sum) return true;
        if(root->left==NULL&&root->right==NULL&&target!=sum) return false;
       
        cout<<target;
        // if(target==sum) return true;
       return a(root->left,target,sum)||a(root->right,target,sum);

    }
    bool hasPathSum(TreeNode* root, int sum) {
        if(root==NULL)
        return false;
        int target=0;
        return a(root,target,sum);
        
    }
};

---

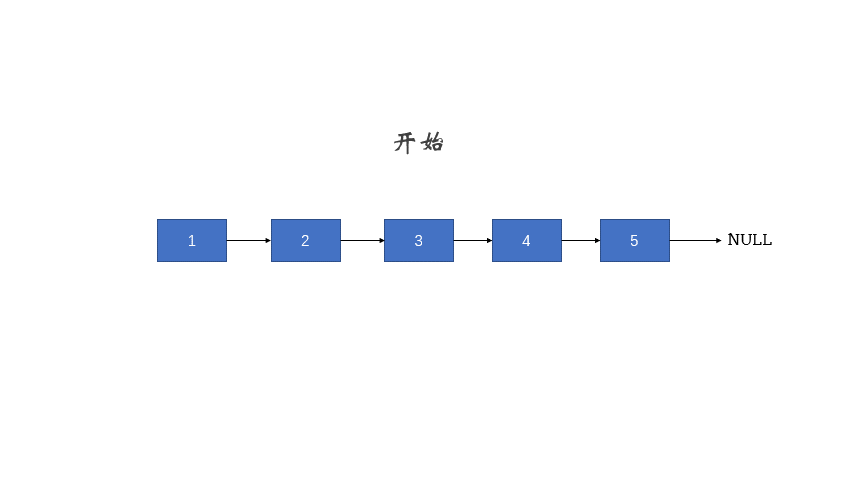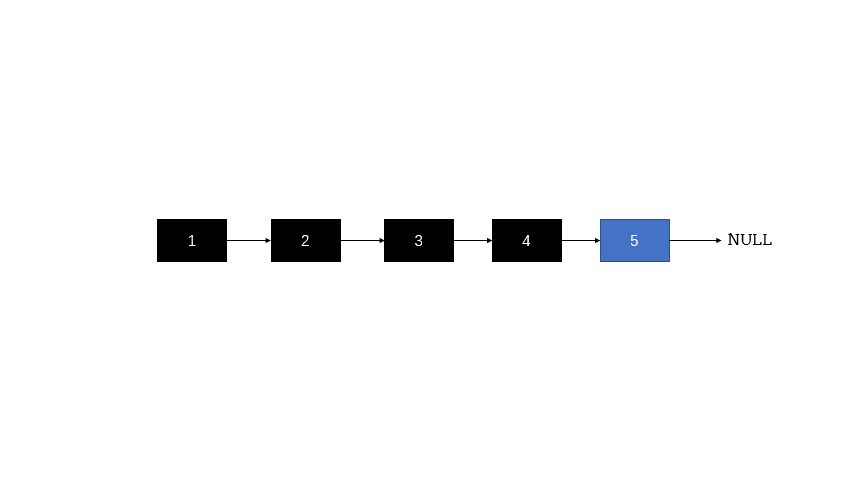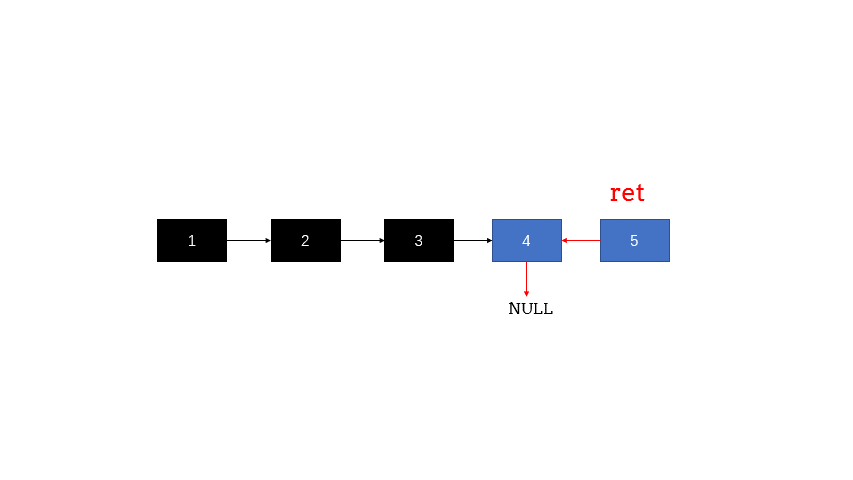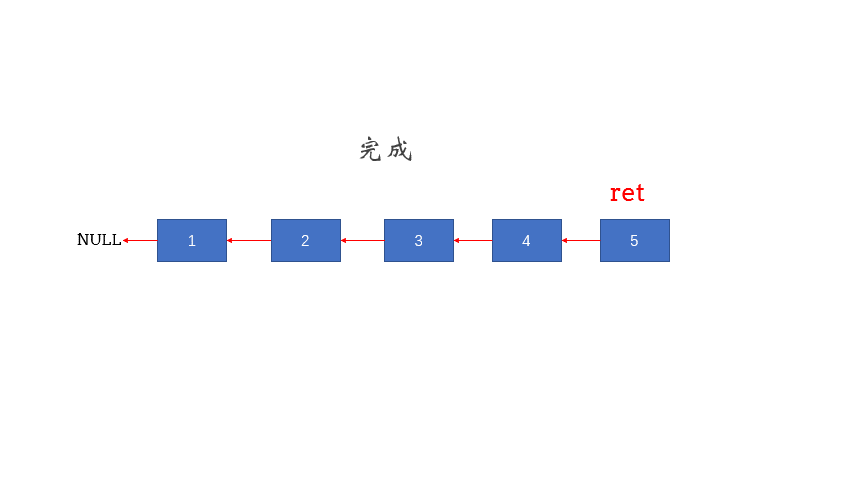
定义一个函数，输入一个链表的头节点，反转该链表并输出反转后链表的头节点。

输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL

这个题目有点意思,因为每一层返回的都是一样的东西,终止条件赋予了返回值

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:

    ListNode* reverseList(ListNode* head) {
        {
         //最后都是返回头指针
         if(head==NULL||head->next==NULL)
        {
            return head;//这里就是给定了头指针

        }
        ListNode* res=reverseList(head->next);//函数的左右每一层都把后面节点的next指向自己,然后自己指向next
        head->next->next=head;
        head->next=NULL;
        return res;//每一层都要返回的是结果的头指针;

        }
    }
    };

图解