Leetcode 递归题目总结

最新推荐文章于 2024-09-20 23:23:51 发布
原创 最新推荐文章于 2024-09-20 23:23:51 发布 · 1.8k 阅读 · 12 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#C++ #总结 #递归

本文总结了递归算法的本质、特点及适用题型，特别关注于二叉树和链表问题。提供了递归解题的模板，并列举了多个LeetCode上的递归题目，包括平衡二叉树、链表操作及其他类型问题。强调递归虽然简洁但效率较低，且易导致栈溢出，建议在某些情况下使用迭代解法。 
    Leetcode上的递归一共有45道，现在刷了一半了，花一天半时间复盘，之后进入下一类题型。

实质

把问题转化为规模缩小了的同类问题的子问题，是一种直接或者间接调用自身的算法。

特点

  • 必须有一个明确的递归结束条件，称为递归出口
  • 递归算法解题通常显得很简洁，但递归算法解题的运行效率较低。所以一般不提倡用递归算法设计程序。（比如在leetcode上用递归求斐波那契数列就溢出）
  • 在递归调用的过程当中系统为每一层的返回点、局部量等开辟了栈来存储。递归次数过多容易造成栈溢出等。所以一般不提倡用递归算法设计程序
  • 原理就是一个栈
  • 好处是：写代码迅速，代码简洁，坏处是：效率低

适合题型

树、二叉树（二叉平衡树、二叉搜索树、满二叉树、普通二叉树）、链表、斐波那契、阶乘

答题模板

思考以下三个问题：

（1） 找终止条件

（2） 找返回值

（3） 本级递归应该做什么。不要考虑过多，只关心本级干什么

这个答题模板参考自三道题套路解决递归问题， 在leetcode的评论区上发现的宝藏，起初我做递归题思路是一团乱麻，看了这个博主的文章受益良多。

可能会用到的技巧

  • 高度平衡二叉树定义为：一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1 。
  • 一颗平衡二叉树的左右子树为平衡二叉树’
  • 二叉搜索树的中序遍历刚好是升序

Leetcode按照类型分组

注意，这些题有些出自深度优先遍历的分组里，要牢记DFS和递归的关系：

​ DFS可以用递归实现，也可以不用递归实现。

1.二叉树
110. 平衡二叉树

​

题目描述
给定一个二叉树，判断它是否是高度平衡的二叉树。本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1 。

​

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
 //深度优先遍历求树高，再根据平衡二叉树的定义判断是否平衡
 /*
 递归停止条件：节点为空；树不平衡
 返回什么：真假
 本级干什么：判左右子树高度相差值<=1 ，判左右子树是否是平衡树
 */
 class Solution {
public:
    bool isBalanced(TreeNode* root) {
        //左右子树均是平衡二叉树
        if(root==nullptr)
            return true;
        if(abs(depth(root->left)-depth(root->right))>1){
            return false;
        }
        return isBalanced(root->left)  &&  isBalanced(root->right);
    }
    int depth(TreeNode* root)
     {
        if(root==nullptr){
            return  0;
        }
        return max(depth(root->left),depth(root->right))+1;
    }
};
111. 二叉树的最小深度
题目描述
给定一个二叉树，找出其最小深度。最小深度是从根节点到最近叶子节点的最短路径上的节点数量。说明：叶子节点是指没有子节点的节点。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
 /*思路：
 终止条件：走到空节点
 返回什么：返回左右子树上的最小深度+1
 本级递归应该做什么：求左右子树上的最小深度
 */
class Solution {
public:

    int minDepth(TreeNode* root) {
        if(root==nullptr)  return  0;
         int left=minDepth(root->left);
         int right=minDepth(root->right);
         if(left==0){     //应对只有右子树的情况
             return right+1;
         }
         if(right==0){  //应对只有左子树的情况
             return left+1;
         }
         return min(right,left)+1;
    }
    
};
226. 翻转二叉树
翻转一棵二叉树。

示例：

输入：

     4
   /   \
  2     7
 / \   / \
1   3 6   9

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
/*
递归终止条件：root为空
返回什么：已经翻转完左右子树的根节点
本级递归做什么： 进行左右子树的翻转，左右子树的根节点的交换
*/
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if(root==nullptr) return  root;
        
        root->left=invertTree(root->left);
        root->right=invertTree(root->right);

        TreeNode* temp=root->right;
        root->right=root->left;
        root->left=temp;

        return root;

        
    }
};
617. 合并二叉树
给定两个二叉树，想象当你将它们中的一个覆盖到另一个上时，两个二叉树的一些节点便会重叠。

你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠，那么将他们的值相加作为节点合并后的新值，否则不为 NULL 的节点将直接作为新二叉树的节点。

示例 1:

输入: 
	Tree 1                     Tree 2                  
          1                         2                             
         / \                       / \                            
        3   2                     1   3                        
       /                           \   \                      
      5                             4   7                  
输出: 
合并后的树:
	     3
	    / \
	   4   5
	  / \   \ 
	 5   4   7
注意: 合并必须从两个树的根节点开始。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
 /*
 递归停止条件：root1和root2有一个为空
 返回什么：返回合并后的树的根节点
 本级递归应该做什么： 合并两个二叉树:
 */
class Solution {
public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        if(!root1)   return root2;
        if(!root2)   return root1;
        
        root1->left=mergeTrees(root1->left,root2->left);
        root1->right=mergeTrees(root1->right,root2->right);
        root1->val=root1->val+root2->val;
        

        return root1;
        

    }   
};
654. 最大二叉树
给定一个不含重复元素的整数数组 nums 。一个以此数组直接递归构建的 最大二叉树 定义如下：

二叉树的根是数组 nums 中的最大元素。
左子树是通过数组中 最大值左边部分 递归构造出的最大二叉树。
右子树是通过数组中 最大值右边部分 递归构造出的最大二叉树。
返回有给定数组 nums 构建的 最大二叉树 。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
 /*
 思路：
 递归停止条件：构树数组为空
 返回什么： 构造的二叉树的根节点：
 本级递归干什么： 求最大值，分别构造左右子树
 */
class Solution {
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        if(nums.size()==0) return NULL;
        return buildtree(nums,0,nums.size()-1);
    }
    TreeNode* buildtree(vector<int>& nums,int l, int r ){
         if(l>r)  return NULL;
         
         int index=l;
         int max=nums[l];
         for(int i=l+1;i<=r;i++){
             if(nums[i]>=max){
                 index=i;
                 max=nums[i];
             }
         }
        TreeNode* root1=new TreeNode();
        root1->left=buildtree(nums,l,index-1);
        root1->right=buildtree(nums,index+1,r);
        root1->val=max;    
        return  root1;

    }
};
199.二叉树的右视图
题目描述
给定一棵二叉树，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。


class Solution {
//根结点 -> 右子树 -> 左子树」 的顺序访问， 就可以保证每层都是最先访问最右边的节点的。
//（与先序遍历 「根结点 -> 左子树 -> 右子树」 正好相反，先序遍历每层最先访问的是最左边的节点）
/*
递归停止条件：节点为空
返回什么：  只是遍历，不用返回
本级干什么：根节点-》右子树-》左子树这样访问二叉树


*/
    List<Integer> res = new ArrayList<>();

    public List<Integer> rightSideView(TreeNode root) {
        dfs(root, 0); // 从根节点开始访问，根节点深度是0
        return res;
    }

    private void dfs(TreeNode root, int depth) {
        if (root == null) {
            return;
        }
        // 先访问 当前节点，再递归地访问 右子树 和 左子树。
        if (depth == res.size()) {   // 如果当前节点所在深度还没有出现在res里，说明在该深度下当前节点是第一个被访问的节点，因此将当前节点加入res中。
            res.add(root.val);
        }
        depth++;
        dfs(root.right, depth);
        dfs(root.left, depth);
    }
}
783. 二叉搜索树节点最小距离
题目描述
给定一个二叉搜索树的根节点 root，返回树中任意两节点的差的最小值。

在这里插入图片描述

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
 /*
 BST的中序遍历结果为节点值升序结果，所以最小距离为升序结果相邻两数的差，所以可以在递归生成中序遍历时求最小差值，从结果集中有两个节点结果时开始计算，求出最小值
 递归：
 停止条件：节点为空
 返回什么：  只是遍历，什么也不返回
 本级递归干什么：中序遍历，并且求相邻节点得差值，记录最小差值，
 */
class Solution {
public:
    int this_min=INT_MAX;
    int  pre=INT_MAX;  //记录升序求差值得前一个值
    int minDiffInBST(TreeNode* root) {
        if(!root)  return INT_MAX;
        dfs(root);
        return this_min;
    }
    void dfs(TreeNode* root){
        if(!root)  return;
        dfs(root->left);
        this_min=min(this_min,abs(root->val-pre));
        pre=root->val;
        dfs(root->right);
    }
};
1379. 找出克隆二叉树中的相同节点
题目描述
给你两棵二叉树，原始树 original 和克隆树 cloned，以及一个位于原始树 original 中的目标节点 target。

其中，克隆树 cloned 是原始树 original 的一个 副本 。

请找出在树 cloned 中，与 target 相同 的节点，并返回对该节点的引用（在 C/C++ 等有指针的语言中返回 节点指针，其他语言返回节点本身）。

在这里插入图片描述

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
//思路：在两颗树中搜索目标节点
/*
递归停止条件：节点为空；找到所求节点
返回什么： 所求节点
本级递归干什么：比较是否找到了，没找到就左右子树递归进行找
*/
class Solution {
public:
    TreeNode* getTargetCopy(TreeNode* original, TreeNode* cloned, TreeNode* target) {
            if(!original || !cloned || !target)  return NULL;

            //判断当前节点是否为所求
            if(original==target){
                return cloned;
            }
            TreeNode* res;
            //在左子树中找
            res=getTargetCopy(original->left,cloned->left,target);
            if(res)  return res;
            //左子树没找到，接着在右子树找
            res=getTargetCopy(original->right,cloned->right,target);
            return res;
    }
};
07. 重建二叉树
题目描述：输入某二叉树的前序遍历和中序遍历的结果，请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

在这里插入图片描述

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
 /*
 递归停止条件：输入列表空了
 返回什么：  树的根节点
 本级递归干什么： 申请当前节点，建立左子树，建立右子树
 */
class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if(!preorder.size())  return NULL;
        return dfs(preorder,inorder,0,preorder.size()-1,0,inorder.size()-1);
       
    }
     TreeNode* dfs(vector<int>& preorder, vector<int>& inorder,int pl, int pr,int il,int ir) {
        if(il>ir)  return NULL;
        //找到根在中序遍历中的索引
        int index=0; 
        for(int i=il;i<=ir;i++){
            if(inorder[i]==preorder[pl]){
                index=i;
                break;
            }
                
        }
        
        //建树
        TreeNode* root=new TreeNode(preorder[pl]); //根节点
        int k=index-il;  //左子树个数
        root->left=dfs(preorder,inorder,pl+1,pl+k,il,index-1);
        root->right=dfs(preorder,inorder,pl+1+k,pr,1+index,ir);
        return root;

     }
};
1038. 把二叉搜索树转换为累加树
题目描述
给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下，二叉搜索树满足下列约束条件：
节点的左子树仅包含键 小于 节点键的节点。
节点的右子树仅包含键 大于 节点键的节点。
左右子树也必须是二叉搜索树。

在这里插入图片描述

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
 /*
 遍历顺序  右节点->根->左节点，对于每一个节点要改的值   当前节点=遍历的前一个节点+当前节点
 递归停止条件：节点为空
 返回什么： 计算好当前累加值的根节点
 本级递归干什么：   求当前节点的累加值，递归左右子树
 */
class Solution {
public:
     TreeNode* pre; //当作游标，遍历时的前一个节点。
    TreeNode* bstToGst(TreeNode* root) {
        if(!root) return NULL;
        root->right=bstToGst(root->right);
        if(pre) root->val=root->val+pre->val;
        pre=root;
        root->left=bstToGst(root->left);
        return root;
    }
};
669. 修剪二叉搜索树
题目描述
给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树不应该改变保留在树中的元素的相对结构（即，如果没有被移除，原有的父代子代关系都应当保留）。 可以证明，存在唯一的答案。
所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

在这里插入图片描述

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
 /*
 递归停止条件：节点为空
 返回什么：修剪好的树的根节点
 本级递归干什么：比较是否在边界区间，当前节点和边界区间的关系只有三种：val在区间内；val小于左区间；val>右区间；
 */
 //当前节点
 
class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if(!root)  return NULL;
        if(root->val < low)  return  trimBST(root->right,low,high);  //val小于左区间
        if(root->val > high) return  trimBST(root->left,low,high);  //val大于右区间

        //val在区间内
        root->left=trimBST(root->left,low,high);
        root->right=trimBST(root->right,low,high);
        return  root;

    }
};
938. 二叉搜索树的范围和
题目描述
给定二叉搜索树的根结点 root，返回值位于范围 [low, high] 之间的所有结点的值的和。

在这里插入图片描述

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
/*
 递归停止条件：节点为空
 返回什么： 范围内节点值和
 本级递归干什么：比较是否在边界区间，当前节点和边界区间的关系只有三种：val在区间内；val小于左区间；val>右区间；
 */

class Solution {
public:
    int rangeSumBST(TreeNode* root, int low, int high) {
   
        if(!root)  return 0;
        if(root->val<low)  return rangeSumBST(root->right,low,high);
        if(root->val>high)  return rangeSumBST(root->left,low,high);
        return   root->val+rangeSumBST(root->left,low,high)+rangeSumBST(root->right,low,high);
        
    }
};
865. 具有所有最深节点的最小子树
题目描述
定一个根为 root 的二叉树，每个节点的深度是 该节点到根的最短距离 。

如果一个节点在 整个树 的任意节点之间具有最大的深度，则该节点是 最深的 。

一个节点的 子树 是该节点加上它的所有后代的集合。

返回能满足 以该节点为根的子树中包含所有最深的节点 这一条件的具有最大深度的节点。

在这里插入图片描述

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
 /*
 返回距离所有最深节点最近的祖父节点（如果仅包含一个最深节点，那就是返回它本身）

递归停止条件：节点为空
返回什么：  含所有最深节点的最近祖父节点
本级递归干什么： 求左右子树高度； 对于一个节点，如果左子树高度==右子树高度，这个节点就是答案，如果左子树高度<右子树高度，查找右子树，否则查找左子树
 */
class Solution {
public:
    TreeNode* subtreeWithAllDeepest(TreeNode* root) {
        if(!root)   return NULL;
        int l_depth=maxdepth(root->left)+1;  //左子树深度
        int  r_depth=maxdepth(root->right)+1;  //右子树深度
        //深度相同，当前节点就是所求
        if(l_depth>r_depth)  root=subtreeWithAllDeepest(root->left); //左子树高，所求一定在左子树
        if(l_depth<r_depth)  root=subtreeWithAllDeepest(root->right);  //右子树高，所求一定在右子树
        return root;
    }
    //求树高
    int maxdepth(TreeNode* root){
        if(!root)  return 0;
        return max(maxdepth(root->left),maxdepth(root->right))+1;
    }
};
894. 所有可能的满二叉树
题目描述
满二叉树是一类二叉树，其中每个结点恰好有 0 或 2 个子结点。

返回包含 N 个结点的所有可能满二叉树的列表。 答案的每个元素都是一个可能树的根结点。

答案中每个树的每个结点都必须有 node.val=0。

你可以按任何顺序返回树的最终列表。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
    /*技巧：偶数个节点构不成满二叉树，因此输入都是奇数，并且把奇数按照1+奇数+奇数的形式分别划分，看有多少个划分方式*/
/*
/*

*/
递归停止条件：构树节点为0
返回什么： 由这些节点可构成的满二叉树的根节点的列表
本级干什么：构造根节点，构造左右子树，拼接
*/
        
public:
    vector<TreeNode*> allPossibleFBT(int N) {
        vector<TreeNode*> res;
        if(N==0)  return res;
        if(N==1){
            TreeNode* root=new TreeNode(0);
            res.push_back(root);
            return res;
        }
        for(int i=1;i<N;i+=2){
            
                vector<TreeNode*> left=allPossibleFBT(i);
                vector<TreeNode*> right=allPossibleFBT(N-1-i);
                for(TreeNode* l:left)
                    for(TreeNode* r:right){
                        TreeNode* thisroot=new TreeNode(0);
                        thisroot->left=l;
                        thisroot->right=r;
                        res.push_back(thisroot);
                    }
        
        }
        return res;
    }
  
};
2.链表
83. 删除排序链表中的重复元素
给定一个排序链表，删除所有重复的元素，使得每个元素只出现一次。

示例 1:

输入: 1->1->2
输出: 1->2
示例 2:

输入: 1->1->2->3->3
输出: 1->2->3

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
 /*
 思路：
 递归停止条件：走到连表尾部
 返回信息： 链表的头节点
 本级递归做什么： 递归删除重复元素，
 */
class Solution {
public:
    ListNode* deleteDuplicates(ListNode* head) {
            if(head==nullptr || head->next==nullptr)  return head;
             if(head->val==head->next->val)  {
                 head=deleteDuplicates(head->next);  //如果有重复元素，删除前边的元素
             }else{
                 head->next=deleteDuplicates(head->next);
             }
             return head;
            
   
    }
};
2. 两数相加
题目描述
给你两个非空的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，并且每个节点只能存储 一位 数字。
请你将两个数相加，并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外，这两个数都不会以 0 开头。
示例
输入：l1 = [2,4,3], l2 = [5,6,4]
输出：[7,0,8]
解释：342 + 465 = 807.
示例 2：

输入：l1 = [0], l2 = [0]
输出：[0]
示例 3：

输入：l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出：[8,9,9,9,0,0,0,1]

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
 /*
 递归结束条件：节点为空
 返回什么：链表头节点
 本级递归干什么：相加当前节点，并且可能进位，进行递归  ：所以需要另外开一个函数
 */
class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
                return recu(l1,l2,0);
    }
    ListNode*  recu(ListNode* l1, ListNode* l2, int a){  //a是进位
        if(!l1 && !l2) {
            if(a==1){
                return new ListNode(a);
            }
            return NULL;
        }
        if(!l1){
            l1=new ListNode(0);
        }
        if(!l2){
            l2=new ListNode(0) ;  //是为了让递归进行下去
        }
        int v=l1->val+l2->val+a;
        l1->val=v%10;
        if(v>=10){
            l1->next=recu(l1->next,l2->next,1);
        }else{
            l1->next=recu(l1->next,l2->next,0);
        }

        return l1;

    }
};
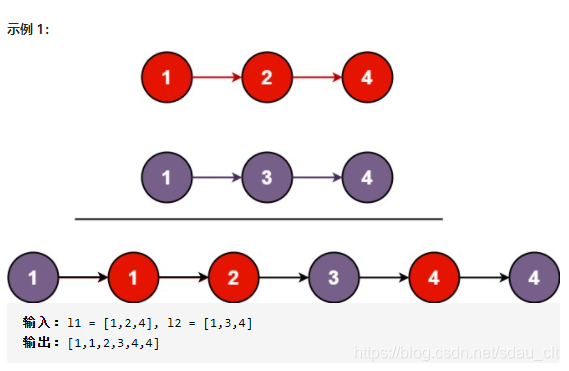
21. 合并两个有序链表
题目描述
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。


/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
 /*
 递归停止条件:至少一个节点为空
 返回什么信息：已经合并后的链表的头节点
 本级递归干什么: 当前较小的节点和下一步递归返回的节点连接
 */
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
            if(!l1)  return l2;
            if(!l2)   return  l1;
            if(l1->val<l2->val){
                l1->next=mergeTwoLists(l1->next,l2);
                return l1;
            }
            l2->next=mergeTwoLists(l1,l2->next);
            return l2;
    }
};
3.其他
17. 电话号码的字母组合
给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。


class Solution {
        unordered_map<string,string> dic{{"2","abc"},{"3","def"},{"4","ghi"},{"5","jkl"},{"6","mno"},{"7","pqrs"},{"8","tuv"},{"9","wxyz"}};
public:
//就好比树的深度优先遍历，将输入转化为字母树，再进行深搜
/*
递归停止条件：  字符串为空；
递归返回什么：  字符串 列表
本级递归干什么： 下一个递归返回的列表和当前字符串进行拼接，返回字符串列表
*/
    vector<string> letterCombinations(string digits) {
            vector<string> res;
            if(digits.size()==0)   //应对初始字符串就是空的情况
                return res;
            string v=string(1,digits[0]);  //digits第一个元素
            if(digits.size()==1){
                for(int j=0;j<dic[v].size();j++){
                        res.push_back(string(1,dic[v][j]));
            }
            return  res;
            }    
            digits.erase(0,1);//删除digits第一个元素
            vector <string> res1=letterCombinations(digits);
            for(int j=0;j<dic[v].size();j++)
                for(int i=0;i<res1.size();i++){
                        res.push_back(string(1,dic[v][j])+res1[i]);
            }
            return  res;
            
    }  
};
面试题 08.05. 递归乘法
题目描述
递归乘法。 写一个递归函数，不使用 * 运算符， 实现两个正整数的相乘。可以使用加号、减号、位移，但要吝啬一些。
示例1:
输入：A = 1, B = 10
输出：10

保证乘法范围不会溢出

class Solution {
public:
    int multiply(int A, int B) {
        if(!A||!B) return 0;
        if(A==1)  return B;
        if(B==1)   return  A;
        return multiply(1,1)+multiply(1,B-1)+multiply(A-1,1)+multiply(A-1,B-1);
    }
};
剑指 Offer 10- I. 斐波那契数列
题目描述
写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项（即 F(N)）。斐波那契数列的定义如下：

F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

示例 1：

输入：n = 2
输出：1

用如下递归会超时

class Solution {
public:
    int fib(int n) {
        if(!n)  return 0;
        if(n==1)  return 1;
        int a=1;
        int b=0;
        for(int i=2;i<=n;i++){  
            a=a+b; 
            b=a-b;
            a=a%1000000007;
        }
        return a;

    }
};

因此选择用迭代

class Solution {
public:
    int fib(int n) {
        if(!n)  return 0;
        if(n==1)  return 1;
        int a=1;
        int b=0;
        for(int i=1;i<n;i++){  //注意这里i<n 而不是 i<=n  举几个例子就明白了 比如f(2)=f(1)+f(0)
            a=a+b; 
            b=a-b;
            a=a%1000000007;
        }
        return a;

    }
};
剑指 Offer 10- II. 青蛙跳台阶问题
题目描述
一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

示例 1：

输入：n = 2
输出：2

和上一题斐波那契数列一个类型的题，同样的用递归会超时，所以选择迭代

class Solution {
    /*对于台阶n
     f(n)=f(n-1)+f(n-2)
         */
public:
    int numWays(int n) {
        if(!n) return 1;
        if(n==1)  return 1;
       
        int a=1;
        int b=1;
        for(int i=2;i<=n;i++){
            a=a+b;
            b=a-b;
            a=a%1000000007;
        }
        return a;
    }
};
1137 .第 N 个泰波那契数
题目描述
泰波那契序列 Tn 定义如下：

T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2

给你整数 n，请返回第 n 个泰波那契数 Tn 的值。

示例 1：

输入：n = 4
输出：4
解释：
T_3 = 0 + 1 + 1 = 2
T_4 = 1 + 1 + 2 = 4

和前边斐波那契和青蛙跳台阶的题类似，用的迭代

class Solution {
    //类比斐波那契数列，f(n)=f(n-1)+f(n-2)
    //这里泰波那契数列, t(n)=t(n-1)+t(n-2)+t(n-3)  
    //同样的道理，这个时间复杂度更大，用递归会超时
public:
    int tribonacci(int n) {
        if(!n)  return 0;
        if(n==1)  return 1;
        if(n==2)  return  1;

        int a=1;
        int b=1;
        int c=0;
        for(int i=3;i<=n;i++){
            int old_a=a;  //以前的a值后边会赋值给b
            a=a+b+c;
            c=b;  //以前的b赋值给c
            b=old_a;
        }
        return a;

    }
};
剑指 Offer 16. 数值的整数次方
题目描述
实现函数double Power(double base, int exponent)，求base的exponent次方。不得使用库函数，同时不需要考虑大数问题。

示例 1:

输入: 2.00000, 10
输出: 1024.00000
示例 2:
说明:

-100.0 < x < 100.0
n 是 32 位有符号整数，其数值范围是 [−231, 231 − 1] 。

class Solution {
public:
    double myPow(double x, int n) {
        if(n==0)  return 1;
        if(n==1)  return x;
        if(n==-1)  return 1/x;  //复数右移还是复数，但是x*x可能会改变最终结果值
        return  n&1? myPow(x*x,n>>1)*x:myPow(x*x,n>>1);
    }
};
//如果每次n-1  x*mypow(x,n-1)会超时，因此想着让X变为	x^2
leetcode之递归刷题总结1
nuist_NJUPT的博客
01-31 1580
leetcode之递归刷题总结1 1-递归乘法 题目链接： 思路：让B-1乘A并递归下去，递归的结果加上A，就是B乘A。 AC代码如下： class Solution { public int multiply(int A, int B) { if(B==0){ return 0 ; } return A + multiply(A,B-1) ; } } 2-预测赢家 题目链接：题目链接戳这里！！！ 思路：如果是偶数个
【LeetCode】递归精选8题——基础递归、链表递归
Qiuhan_909的博客
02-20 3940
LeetCode 递归精选8题（包含基础递归、链表递归） 详解
leetcode - 递归
mike_jun的博客
03-15 667
目录 98.验证搜索二叉树 22.括号生成 100.相同的树 101.对称二叉树 104.树的最大深度 108.将有序数组转换成搜索二叉树 110.平衡二叉树 111.二叉树的最小深度 112.路径总和 226.翻转二叉树 98.验证搜索二叉树 给定一个二叉树，判断其是否是一个有效的二叉搜索树。 假设一个二叉搜索树具有如下特征： 节点的左子树只包含小于当前节点的数。 ...
Leetcode-递归
qq_49723651的博客
02-07 689
文章目录q21 合并两个有序链表q101 对称二叉树q104 二叉树的最大深度q226 翻转二叉树q236 二叉树的最近公共祖先 q21 合并两个有序链表 题目传送门 题解 可以使用递归和迭代两种方法进行求解，两种方法都比较简单。 递归： func mergeTwoLists(l1 *ListNode, l2 *ListNode) *ListNode { if l1 == nil { return l2 } else if l2 == nil { return l1 } else if
LeetCode专题----递归
changetocs的博客
12-24 1001
1、111. Minimum Depth of Binary Tree Given a binary tree, find its minimum depth.The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node. 分析：在
LeetCode 中有关递归的题目
ForeverSen的博客
07-31 812
递归，其实就是在运行的过程中调用自己。 构成递归需具备的条件： 子问题须与原始问题为同样的事，且更为简单； 不能无限制地调用本身，须有个出口，化简为非递归状况处理。 112. 路径总和 题目描述： 给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。 说明: 叶子节点是指没有子节点的节点。 示例: 给定如下二叉树，以及目标和 sum = 2...
精选资源
leetcode分类-leetcode:Leetcode题目分类总结，附题解及思路
06-30
《LeetCode题目分类总结与解题思路探讨》 LeetCode，作为全球知名的技术学习平台，以其海量的编程挑战题目深受广大程序员喜爱。它涵盖了多种编程语言，如Java、Python、C++等，提供了丰富的算法和数据结构问题，...
精选资源
Leetcode所有题目和解答（多语言实现）.rar
06-24
本压缩包“Leetcode所有题目和解答（多语言实现）.rar”包含了LeetCode上的所有题目及其多种编程语言的解决方案，对于学习者来说，这是一个极其宝贵的资源库。 首先，让我们深入了解一下LeetCode中的主要知识点： ...
leetcode递归专题-leetcode:不定期发布leetcode解题思路和代码
06-30
leetcode递归专题 leetcode 我的LeetCode主页： 不定期发布leetcode解题思路和代码 一些好的题目 动态规划 一般dp 区间dp 位数dp 状压dp 树形DP 树 二叉树 前缀树 -- 其他树上问题 ---- ---- ---- ---- ---- ---- --...
LeetCode之递归算法
ZHOUJIAN_TANK的博客
07-23 431
递归三步曲 何为递归？程序反复调用自身即是递归。 我自己在刚开始解决递归问题的时候，总是去纠结这一层函数做了什么，它调用自身后的下一层函数又做了什么。。。。然后就会觉得实现一个递归解法十分复杂，根本就无法下手。 这是一个思维误区，一定要走出来，既然递归是一个反复调用自身的过程，这就是说它的每一及的功能都是一样的，因此我们只需要关注一级递归的解决过程即可 如上图所示，我们需要关心的主要是以下三点 整个递归的终止条件 一级递归需要做什么 应该返回给上一级的返回值是什么 因此，也就有了我们解递归题的三步
LeetCode刷题记录--递归
m0_67739923的博客
04-16 3005
数位dp，博弈，约瑟夫环
Leetcode 递归题
YenKoc的博客
02-04 323
24. 两两交换链表中的节点 题目描述： 给定一个链表，两两交换其中相邻的节点，并返回交换后的链表。 你不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。 示例: 给定 1->2->3->4, 你应该返回 2->1->4->3. 思路分析： 1.链表和树的结构很适合递归，可以往这方面去想。 2.递归首先先想着结束的条件是啥。 3.之...
leetcode之递归详解
ahelloyou的博客
06-24 479
递归 其实递归和二叉树遍历很像,要理解递归,就要理解二叉树遍历. 可以看看这个理解一下 首先说明一个问题，简单阐述一下递归，分治算法，动态规划，贪心算法这几个东西的区别和联系，心里有个印象就好。 递归这种尽量能不用就不用,有时候会造成过大的额外开销以及栈溢出,可以根据这个思想选用贪心算法,动态规划,bfs,dfs等 递归是一种编程技巧，一种解决问题的思维方式；分治算法和动态规划很大程度上是递归思想基础上的（虽然动态规划的最终版本大都不是递归了，但解题思想离不开递归），解决更具体问题的两类算法思想；贪心算法是
Leetcode算法基础篇-递归算法
最新发布
deardeer的博客
09-20 874
递归（Recursion）：指的是一种通过重复的方法。在绝大数编程语言中，可以通过在函数中再次调用函数自身的方式来实现递归。
LeetCode 刷题 -- 递归
qq_43325216的博客
09-28 1317
在上述代码的递归调用里，调用的是f(n-1)和f(n-2)，但是在f(n-1)的递归里面，f(n-2)其实已经计算过了，但是后面还会重复计算。如果最后一步走1个台阶，那么就是n=n-1时候的方法，如果最后一步走2个台阶，那么就是n=n-2的方法，因此 f(n)=f(n-1)+f(n-2)3、如果只有一个节点为null，这种是需要调换左右节点的，假设左节点不为null，右节点为null，那么调换之后，左节点为null，右节点不为null，因此可以不需要特殊处理。）同时，这个节点的子节点也要进行相同的操作。
LeetCode——有关递归的相关题目
Tiffany学习的博客
06-27 612
最近发现自己并没有真正理解递归，于是重新把递归的相关题目又重新做了一遍，参考了http://39.96.217.32/blog/4#comment-container讲解，很受用 111. 二叉树的最小深度 这道题有一个陷阱就是当根节点只有左子树或者只有右子树的时候，最小深度是2，而不是1，所以我决定单独判断这两种情况 /** * Definition for a binary tree...
leetcode——递归
weixin_40906441的博客
03-18 201
1.区别 1）程序结构不同 递归是重复调用 函数自身 实现循环。 迭代是函数内某段代码实现循环。 其中，迭代与普通循环的区别是：迭代时，循环代码中参与运算的变量同时是保存结果的变量，当前保存的结果作为下一次循环计算的初始值。 2）算法结束方式不同 递归循环中，遇到满足终止条件的情况时 逐层返回 来结束。 迭代则根据语句条件判断是否 直接结束循环。 2.递归 一个大问题是否可分解为子问题 子问题的解决方法是否和大问题相同 找到终止条件 ...
五个递归题总结
weixin_30832405的博客
03-20 248
递归 电影院 求阶乘 斐波那契数 数字反转 求台阶走法数 当然，很多递归都是可以优化的，比如f(n)=f(n-1)+f(n-2),这里f(n-2)就会计算两次，可以用散列表存储已经计算的数据，但是这里主要演示递归思想，不再进行优化。 电影院 周末你带着女朋友去电影院，女朋友问你，咱们现在坐在第几排啊，电影院太黑没法数怎么办，于是你问前一排的人他是第几排，你只需要在他的数字上加一就知道自己...
Leetcode——递归案例归纳总结
怡宝2号
05-07 581
1.汉诺塔 有三根杆子A，B，C。A杆上有N个(N>1)穿孔圆盘，盘的尺寸由下到上依次变小。要求按下列规则将所有圆盘移至C杆： 1.每次只能移动一个圆盘. 2.大盘不能叠在小盘上面. 思路 当有N个圆盘在A上, 我们已经找到办法将其移到C杠上了, 我们怎么移动N+1个圆盘到C杠上呢? 很简单, 我们首先用将N个圆盘移动到C上的方法将N个圆盘都移动到B上, 然后再把第N+1个圆盘(最后一个)...
每日LeetCode编程题目实践与总结仓库
- **难度**：LeetCode 题目通常会标明难度等级，从简单（Easy）、中等（Medium）到困难（Hard），这有助于解题者根据自身能力挑选合适的题目。本文件描述中所有题目难度均为「简单」，适合初学者逐步提升。 - **...
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值