线性回归 波士顿房价预测

目录

 

线性回归对波士顿房价进行预测

一、基础概念：

1. 线性回归

2. 平均绝对误差，均方误差的理解

         3. 决定系数

二、实验步骤与分析

1. 数据背景

2. 数据读入

3. 定义特征值、目标值

4. 区分训练集和测试集

5. 线性回归

6. 进行预测

7. 获取平均值

8. 获取均分绝对误差

---

线性回归对波士顿房价进行预测

一、基础概念：

1. 线性回归

回归分析，数理统计学中，回归分析着重在寻求变量之间近似的函数关系。

线性回归分析，就是寻求变量之间近似的线性函数关系。

线性回归就是回归函数为线性函数的情形。

2. 平均绝对误差，均方误差的理解

平均绝对误差（MAE）是一种线性分数，所有个体差异在平均值上的权重都相等。表示预测值和观测值之间绝对误差的平均值。

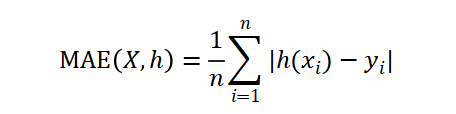
均方误差（MSE）即方差，MSE表示预测数据和原始数据对应点误差的平方和的均值。

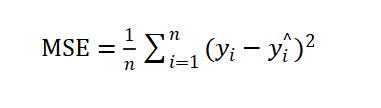，其中n为样本的个数。

线性回归中，MSE（L2损失）计算简便，但MAE（L1损失）对异常点有更好的鲁棒性。当预测值和真实值接近时，误差的方差较小；反之误差方差非常大，相比于MAE，使用MSE会导致异常点有更大的权重，因此数据有异常点时，使用MAE损失函数更好。

3. 决定系数

利用决定系数来量化本次实验中的线性回归模型的表现，表示的是目标变量的预测值和实际值之间的相关程度平方的百分比。决定系数为1的模型表示可以对目标变量进行完美的预测；为0时则很难预测，换用其他标准预测；在0到1之间则表示模型中目标变量有百分之多少可以由选定的特征值来预测。

 

二、实验步骤与分析

主要从以下八个方面来对本次内容进行实验。

序号	任务名称	任务具体要求
1	数据理解	理解数据集背景以及数据含义。
2	数据读入	使用pandas 读入数据并输出读入的数据
3