P7909 [CSP-J 2021] 分糖果

题目背景

红太阳幼儿园的小朋友们开始分糖果啦！

题目描述

红太阳幼儿园有 nn 个小朋友，你是其中之一。保证 n \ge 2n≥2。

有一天你在幼儿园的后花园里发现无穷多颗糖果，你打算拿一些糖果回去分给幼儿园的小朋友们。

由于你只是个平平无奇的幼儿园小朋友，所以你的体力有限，至多只能拿 RR 块糖回去。

但是拿的太少不够分的，所以你至少要拿 LL 块糖回去。保证 n \le L \le Rn≤L≤R。

也就是说，如果你拿了 kk 块糖，那么你需要保证 L \le k \le RL≤k≤R。

如果你拿了 kk 块糖，你将把这 kk 块糖放到篮子里，并要求大家按照如下方案分糖果：只要篮子里有不少于 nn 块糖果，幼儿园的所有 nn 个小朋友（包括你自己）都从篮子中拿走恰好一块糖，直到篮子里的糖数量少于 nn 块。此时篮子里剩余的糖果均归你所有——这些糖果是作为你搬糖果的奖励。

作为幼儿园高质量小朋友，你希望让作为你搬糖果的奖励的糖果数量（而不是你最后获得的总糖果数量！）尽可能多；因此你需要写一个程序，依次输入 n, L, Rn,L,R，并输出你最多能获得多少作为你搬糖果的奖励的糖果数量。

输入格式

输入一行，包含三个正整数 n, L, Rn,L,R，分别表示小朋友的个数、糖果数量的下界和上界。

输出格式

输出一行一个整数，表示你最多能获得的作为你搬糖果的奖励的糖果数量。

输入输出样例

输入 

7 16 23

输出 

6

输入 

10 14 18

输出 

8

输入 #3复制

见附件中的 candy/candy3.in。

输出 #3复制

见附件中的 candy/candy3.ans。

说明/提示

【样例解释 #1】

拿 k = 20k=20 块糖放入篮子里。

篮子里现在糖果数 20 \ge n = 720≥n=7，因此所有小朋友获得一块糖；

篮子里现在糖果数变成 13 \ge n = 713≥n=7，因此所有小朋友获得一块糖；

篮子里现在糖果数变成 6 < n = 76<n=7，因此这 66 块糖是作为你搬糖果的奖励。

容易发现，你获得的作为你搬糖果的奖励的糖果数量不可能超过 66 块（不然，篮子里的糖果数量最后仍然不少于 nn，需要继续每个小朋友拿一块），因此答案是 66。

【样例解释 #2】

容易发现，当你拿的糖数量 kk 满足 14 = L \le k \le R = 1814=L≤k≤R=18 时，所有小朋友获得一块糖后，剩下的 k - 10k−10 块糖总是作为你搬糖果的奖励的糖果数量，因此拿 k = 18k=18 块是最优解，答案是 88。

【数据范围】

测试点	n \len≤	R \leR≤	R - L \leR−L≤
11	22	55	55
22	55	1010	1010
33	{10}^3103	{10}^3103	{10}^3103
44	{10}^5105	{10}^5105	{10}^5105
55	{10}^3103	{10}^9109	00
66	{10}^3103	{10}^9109	{10}^3103
77	{10}^5105	{10}^9109	{10}^5105
88	{10}^9109	{10}^9109	{10}^9109
99	{10}^9109	{10}^9109	{10}^9109
1010	{10}^9109	{10}^9109	{10}^9109

对于所有数据，保证 2 \le n \le L \le R \le {10}^92≤n≤L≤R≤109（原题出自洛谷）

思路

这道题很多人可能看的有点不太懂

但实际上实在说给定一个范围L——R

从中找到一个数减去人数使其余数最多

这一看

？？？

这不就是典型的模拟吗

n  L  R

7 16 23

在L——R这个范围中

有

16 17 18 19 20 21 22 23

16%7=2

17%7=3

18%7=4

19%7=5

20%7=6

21%7=0

22%7=1

23%7=2

所以结果就是6

因此

我们只用一个for和maxn就可以解决了

代码

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int l,r,n,maxn=-1;//定义变量
    cin>>n>>l>>r;//输入人数和边界
    for(int i=l;i<=r;i++)//对边界进行遍历，寻找最大值
    {
        if(i%n>maxn)maxn=i%n;//如果新的值大于存储的，那么更新maxn
    }
    cout<<maxn;//输出
    return 0;
}

但是

csp的题可能这么简单吗

答案是NO

看看题目中最下面的提示

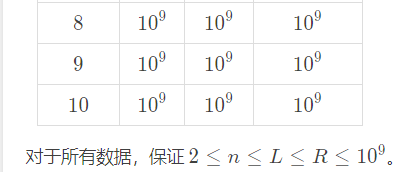
 10^9

记住它

因为它会让你拿90分

没错

它

超时了.....

原因

很简单

时间限制是10^8

所以暴力模拟肯定是行不通的

这个时候我们再看样例

n  L  R

7 16 23

有

16 17 18 19 20 21 22 23

16%7=2

17%7=3

18%7=4

19%7=5

20%7=6

21%7=0

22%7=1

23%7=2

发现没有

它是有巧算方式的

20%7=6  20/7=2(默认int)

22%7=1   22/7=3

他们是不同的两个”界“

16%7=2 20/7=2

17%7=3 20/7=2

18%7=4 20/7=2

19%7=5 20/7=2

20%7=6 20/7=2（只看这一部分）

21%7=0 22/7=3

22%7=1 22/7=3 

23%7=2 22/7=3

而且当他们在一个界中

最多的总是r%n

如果不在同一个界中

如样例所示

最大的总是n-1

可以直接试一下

所以就有了新的判断方式

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int l,r,n;//定义变量
    cin>>n>>l>>r;//输入人数和边界
    if(l/n==r/n)//直接判断
    {
        cout<<r%n;//如果是在同一范围那么输出余数
    } 
    else
    {
        cout<<n-1;//否则输出 人数-1
    }
    return 0;
}

 最后，喜提AC