洛谷P7909 [CSP-J 2021] 分糖果题解

最新推荐文章于 2024-08-19 17:33:48 发布
原创 最新推荐文章于 2024-08-19 17:33:48 发布 · 2.1k 阅读 · 0 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#算法 #c++

1.题目链接

P7909 [CSP-J 2021] 分糖果

2.题意简述

输入n,L,R，在[L,R]中找到一个值k，使得 k mod n 值最大，并将此值输出
注：mod为取模运算符

3.样例解读

样例解读

  • 样例1中，n=7,L=16,R=23，其意思为在16～23中找到一个数字k，使得 k mod n 的值最大，通过计算发现当k=20时，20 mod 7=6，则输出6，祥见下方图表
    样例一
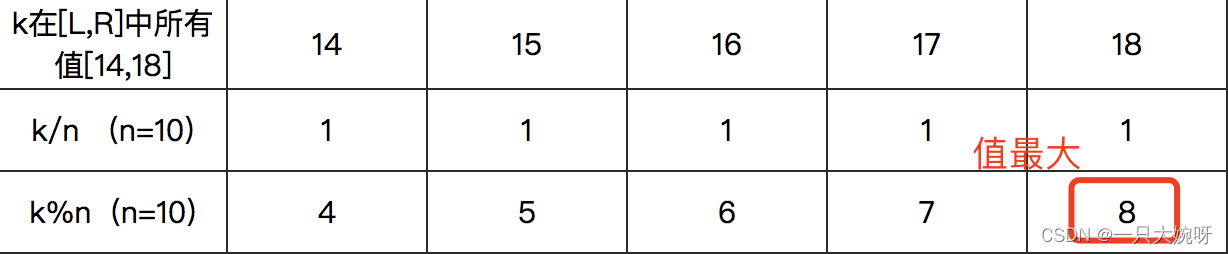
  • 样例2中，n=10,L=14,R=18，其意思为在14～18中找到一个数字课k，使得 k mod n 的值最大，通过计算发现当k=18时，18 mod 10=8，则输出8，详见下方图表
    样例二

4.解题思路

  • 读完此题并结合样例理解题意后，可能会优先考虑暴力枚举，枚举[L,R]中的所有值，找到符合题意的结果，但需注意的是题目中的数据范围： 2 ≤ n ≤ L ≤ R ≤ 1 0 9 2\leq n\leq{L} \leq R \leq10^9 2≤
最低0.47元/天 解锁文章
CSP-J2021普及组题解T1：分糖果
少儿编程乔老师
03-14 7458
CSP-J2021普及组题解T1：分糖果，余数性质。
2021 CCF CSP-J2
c++信息学奥赛
03-16 1274
CSP-J 2021
P7909 [CSP-J 2021] 分糖果
pi314159265a的博客
08-19 1523
）尽可能多；因此你需要写一个程序，依次输入n,L,R，并输出你最多能获得多少。
P7909 [CSP-J 2021] 分糖果（详细讲解）
yaozhiyuannb的博客
08-20 1589
不难发现，如果l与n的余数和r与n的余数相同（在同一个周期范围，同学们平均分拿到的糖果一样），搬糖果的奖励的糖果数量就是最大数与人数的余数，那如果范围比较大，选择范围就多了，搬糖果的奖励的糖果数量就会达到最大值：n-1，因为只要找到余数最多的情况就行了。
2021CSP-J普及组复赛-第一题：分糖果
m0_46183615的博客
05-29 999
2021CSP-J普及组复赛-第一题：分糖果
P7909 [CSP-J 2021] 分糖果 题解
yaosichengalpha的博客
06-27 1163
P7909 [CSP-J 2021] 分糖果 题解
【CSP-J 2021】 分糖果
weixin_60849605的博客
10-27 655
【CSP-J 2021】 分糖果 解题报告
CSP-J 2021 T1 分糖果
小 P 的博客
03-08 1018
CSP-J 2021 T1 题解，它来了 ！！！
CSP-j2021-T1 分糖果题解
cqr__的博客
10-26 2716
题目描述 红太阳幼儿园有n个小朋友，你是其中之一。保证n≥2。 有一天你在幼儿园的后花园里发现无穷多颗糖果，你打算拿一些糖果回去分给幼儿园的小朋友们。 由于你只是个平平无奇的幼儿园小朋友，所以你的体力有限，至多只能拿RR块糖回去。 但是拿的太少不够分的，所以你至少要拿LL块糖回去。保证n≤L≤R 也就是说，如果你拿了kk块糖，那么你需要保证L≤K≤R 如果你拿了kk块糖，你将把这kk块糖放到篮子里，并要求大家按照如下方案分糖果：只要篮子里有不少于nn块糖果，幼儿园的所...
CSP-J 2021真题——分糖果
PanDaoxi
10-31 1297
CSP-J 2021真题——分糖果！
CSP-J2021 A. 分糖果
一枚蒟蒻君的博客
11-24 1548
题目背景 红太阳幼儿园的小朋友们开始分糖果啦！ 题目描述 红太阳幼儿园有n个小朋友，你是其中之一。保证n≥2。 有一天你在幼儿园的后花园里发现无穷多颗糖果，你打算拿一些糖果回去分给幼儿园的小朋友们。 由于你只是个平平无奇的幼儿园小朋友，所以你的体力有限，至多只能拿R块糖回去。 但是拿的太少不够分的，所以你至少要拿L块糖回去。保证nL R n≤L≤R。也就是说，如果你拿了k块糖，那么你需要保证L≤k≤R。 如果你拿了k块糖，你将把这k块糖放到篮子里，并要求大家按照如下方案分糖果：只要篮子里有不.
2021年-分糖果
weixin_60869516的博客
08-27 782
第一题
【洛谷】分糖果
balbalbalabl的博客
12-22 519
数学，暴力。
P7909 [CSP-J 2021] 分糖果 洛谷——规定范围内求mod n 的最大值
m0_62331212的博客
01-16 372
题目——一个不错的积累经验方法 思路 求最后篮子里剩下最多的糖果，即mod n最大值，所以两种情况 1) 最优情况 剩下n-1个糖果 2）达不到n-1个时，r最大的时候剩下的糖果最多 min(r,l+n-1-l%n) #include<algorithm> #include<cstdio> #include<iostream> using namespace std; int main() { int n,l,r...
洛谷P7909 分糖果
Liu92400102的博客
08-09 483
洛谷P7909 分糖果
CSP-J P1 分糖果（洛谷P7909）
SSL_lwz的博客
10-25 2506
提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档 文章目录 前言 一、pandas是什么？ 二、使用步骤 1.引入库 2.读入数据 总结 提示：这里可以添加本文要记录的大概内容： 例如：随着人工智能的不断发展，机器学习这门技术也越来越重要，很多人都开启了学习机器学习，本文就介绍了机器学习的基础内容。 提示：以下是本篇文章正文内容，下面案例可供参考 一、题目： 题目背景 红太阳幼儿园的小朋友们开始分糖果啦！ 题目描述 红太阳幼儿园有nn个小朋友..
[CSP-J 2021] 分糖果c++
最新发布
07-20
### 问题解析 CSP-J 2021 中的“分糖果”问题要求找出在给定范围内，某个孩子能够获得的最多剩余糖果数。题目中，糖果总数为 $ n $，孩子可以选择的糖果数量范围为 $ l $ 到 $ r $。每次分配糖果时，孩子只能获得所选糖果数对 $ n $ 取模后的余数。因此，目标是找出在这个区间内，取模后余数最大的值。 ### 解题思路 1. **取模运算特性**： - 对于任意整数 $ i $，其对 $ n $ 取模的结果 $ i \% n $ 的范围是 $ 0 $ 到 $ n-1 $。 - 在区间 $ l $ 到 $ r $ 内，寻找最大余数时，可以利用取模运算的周期性特性。 2. **优化策略**： - 如果区间长度 $ r - l + 1 \geq n $，那么区间中一定包含一个完整的模 $ n $ 周期，因此最大余数为 $ n-1 $。 - 如果区间长度小于 $ n $，则需要遍历该区间，计算每个值的模 $ n $ 余数，并找出最大值。 ### C++ 实现 #### 方法一：暴力枚举 适用于较小数据范围的解法，直接遍历 $ l $ 到 $ r $ 的所有值，计算其模 $ n $ 的余数，并记录最大值。 ```cpp #include <bits/stdc++.h> using namespace std; int main() { int n, l, r; cin >> n >> l >> r; int max_remainder = 0; for (int i = l; i <= r; i++) { max_remainder = max(max_remainder, i % n); } cout << max_remainder << endl; return 0; } ``` #### 方法二：优化解法 根据模运算的特性，当区间长度 $ r - l + 1 \geq n $ 时，可以直接输出 $ n-1 $；否则，遍历区间并计算最大余数。 ```cpp #include <bits/stdc++.h> using namespace std; int main() { int n, l, r; cin >> n >> l >> r; if (r - l + 1 >= n) { cout << n - 1 << endl; } else { int max_remainder = 0; for (int i = l; i <= r; i++) { max_remainder = max(max_remainder, i % n); } cout << max_remainder << endl; } return 0; } ``` ### 时间复杂度分析 - **暴力枚举**：时间复杂度为 $ O(r-l+1) $，最坏情况下可能达到 $ O(n) $。 - **优化解法**：时间复杂度为 $ O(1) $，当区间长度 $ r - l + 1 \geq n $ 时直接输出结果，否则遍历区间，时间复杂度为 $ O(r-l+1) $。 ### 空间复杂度分析 - 两种方法的空间复杂度均为 $ O(1) $，仅使用了常量级别的额外空间。 ### 总结 通过分析模运算的特性，可以高效地解决“分糖果”问题。对于大规模数据，优化解法显著减少了计算时间，避免了不必要的遍历操作。
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值