~量子编程~固定代码如何输出不确定结果但逻辑一致？？？绕口啊^_^

最新推荐文章于 2023-12-27 17:52:20 发布

原创最新推荐文章于 2023-12-27 17:52:20 发布 · 1.4k 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#量子编程

本文介绍了量子编程的基础概念，并通过中国科学技术大学的'九章'量子计算机实例展示了量子计算的高效性。文章提供了多个量子编程案例，包括简单的量子门操作、量子隐形传态、量子傅立叶变换等，旨在引导读者入门量子计算，并预览未来量子互联网时代的信息动态传输特点。

量子编程公开课现在越来越多了，之前博文（从2050回顾2020，职业规划与技术路径）提及一句：

量子计算机是实现智联网的关键，量子机器人是实现移动智联网的关键。现有技术网络上传输的信息是不变的，智联网时代网络上传输的信息是动态的，端端之间是活的信息。

更多内容参考九章量子计算机：

中国科学技术大学的潘建伟、陆朝阳等人构建了一台76个光子100个模式的量子计算机“九章”，它处理“高斯玻色取样”的速度比目前最快的超级计算机“富岳”快一百万亿倍。也就是说，超级计算机需要一亿年完成的任务，“九章”只需一分钟。同时，“九章”也等效地比谷歌去年发布的53个超导比特量子计算机原型机“悬铃木”快一百亿倍。

博文中关于量子相关博客如下：

量子编程3个最高赞的案例分享:https://blog.youkuaiyun.com/zhangrelay/article/details/103050985

但是并未作任何解释，本文写一点相关内容，抛砖引玉^_^

全部操作视频录像如下：

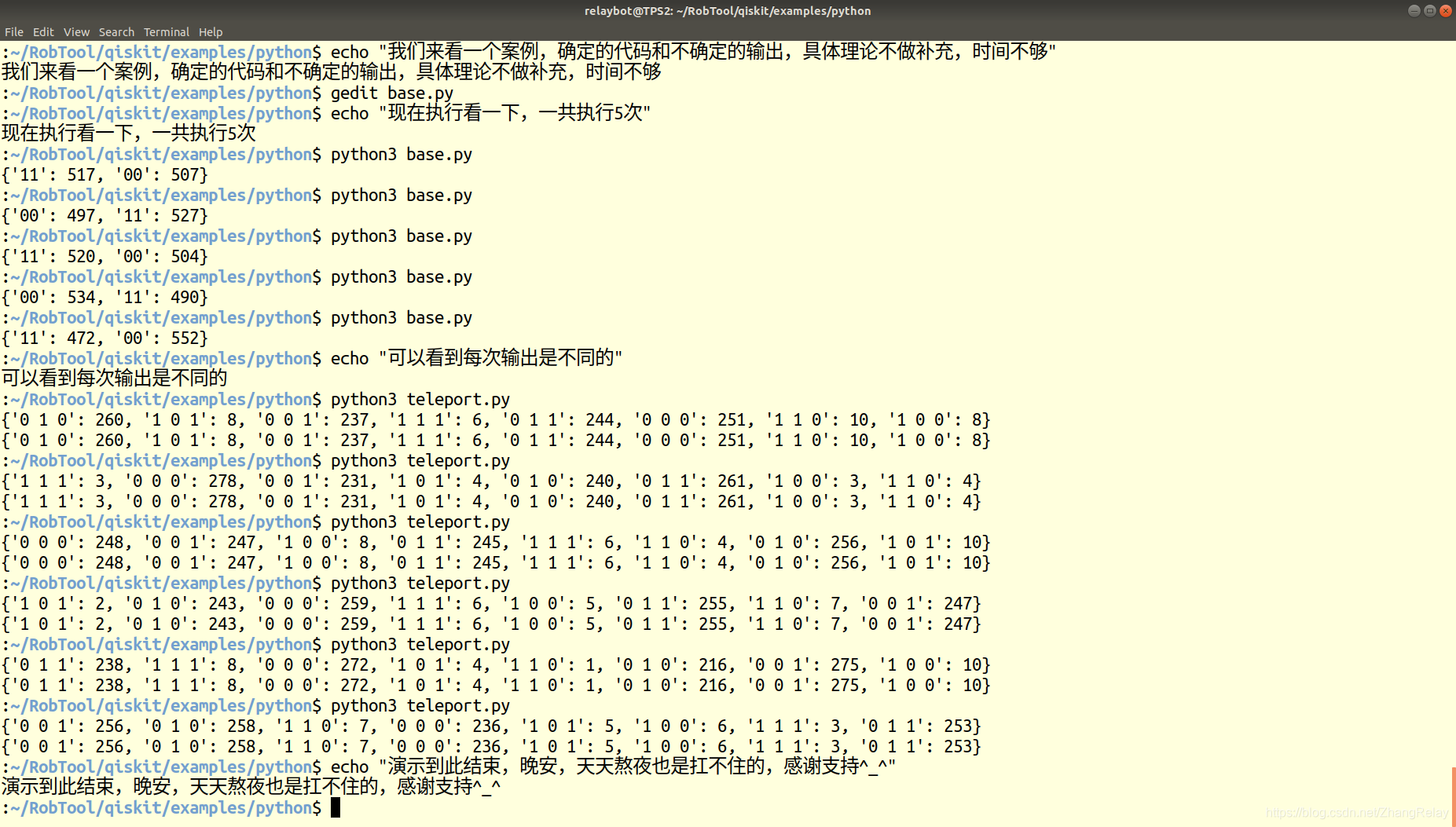
通过量子编程输出演示确定程序对应不确定结果（活的信息）

先是一个简单案例，base.py：

from qiskit import *
qc = QuantumCircuit(2, 2)
qc.h(0)
qc.cx(0, 1)
qc.measure([0,1], [0,1])
backend_sim = BasicAer.get_backend('qasm_simulator')
result = execute(qc, backend_sim).result()
print(result.get_counts(qc))

然后是一个复杂一些的案例，teleport.py：

# -*- coding: utf-8 -*-

# This code is part of Qiskit.
#
# (C) Copyright IBM 2017.
#
# This code is licensed under the Apache License, Version 2.0. You may
# obtain a copy of this license in the LICENSE.txt file in the root directory
# of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
#
# Any modifications or derivative works of this code must retain this
# copyright notice, and modified files need to carry a notice indicating
# that they have been altered from the originals.

"""
Quantum teleportation example.

Note: if you have only cloned the Qiskit repository but not
used `pip install`, the examples only work from the root directory.
"""

from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit
from qiskit import BasicAer
from qiskit import execute

###############################################################
# Set the backend name and coupling map.
###############################################################
coupling_map = [[0, 1], [0, 2], [1, 2], [3, 2], [3, 4], [4, 2]]
backend = BasicAer.get_backend("qasm_simulator")

###############################################################
# Make a quantum program for quantum teleportation.
###############################################################
q = QuantumRegister(3, "q")
c0 = ClassicalRegister(1, "c0")
c1 = ClassicalRegister(1, "c1")
c2 = ClassicalRegister(1, "c2")
qc = QuantumCircuit(q, c0, c1, c2, name="teleport")

# Prepare an initial state
qc.u3(0.3, 0.2, 0.1, q[0])

# Prepare a Bell pair
qc.h(q[1])
qc.cx(q[1], q[2])

# Barrier following state preparation
qc.barrier(q)

# Measure in the Bell basis
qc.cx(q[0], q[1])
qc.h(q[0])
qc.measure(q[0], c0[0])
qc.measure(q[1], c1[0])

# Apply a correction
qc.barrier(q)
qc.z(q[2]).c_if(c0, 1)
qc.x(q[2]).c_if(c1, 1)
qc.measure(q[2], c2[0])

###############################################################
# Execute.
# Experiment does not support feedback, so we use the simulator
###############################################################

# First version: not mapped
initial_layout = {q[0]: 0,
                  q[1]: 1,
                  q[2]: 2}
job = execute(qc, backend=backend, coupling_map=None, shots=1024,
              initial_layout=initial_layout)

result = job.result()
print(result.get_counts(qc))

# Second version: mapped to 2x8 array coupling graph
job = execute(qc, backend=backend, coupling_map=coupling_map, shots=1024,
              initial_layout=initial_layout)
result = job.result()
print(result.get_counts(qc))
# Both versions should give the same distribution

当然，官方教程里还有很多示例，分别如下，有兴趣推荐自学哦，10年以后的量子计算机都会用类似模式编程算法的^_^

circuit_draw.py

# -*- coding: utf-8 -*-

# This code is part of Qiskit.
#
# (C) Copyright IBM 2017, 2018.
#
# This code is licensed under the Apache License, Version 2.0. You may
# obtain a copy of this license in the LICENSE.txt file in the root directory
# of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
#
# Any modifications or derivative works of this code must retain this
# copyright notice, and modified files need to carry a notice indicating
# that they have been altered from the originals.

"""
Example showing how to draw a quantum circuit using Qiskit.
"""

from qiskit import QuantumCircuit


def build_bell_circuit():
    """Returns a circuit putting 2 qubits in the Bell state."""
    qc = QuantumCircuit(2, 2)
    qc.h(0)
    qc.cx(0, 1)
    qc.measure([0, 1], [0, 1])
    return qc

# Create the circuit
bell_circuit = build_bell_circuit()

# Use the internal .draw() to print the circuit
print(bell_circuit)

commutation_relation.py

# -*- coding: utf-8 -*-

# This code is part of Qiskit.
#
# (C) Copyright IBM 2017, 2018.
#
# This code is licensed under the Apache License, Version 2.0. You may
# obtain a copy of this license in the LICENSE.txt file in the root directory
# of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
#
# Any modifications or derivative works of this code must retain this
# copyright notice, and modified files need to carry a notice indicating
# that they have been altered from the originals.

from qiskit import *

from qiskit.transpiler import PassManager
from qiskit.transpiler.passes import CommutationAnalysis, CommutativeCancellation

circuit = QuantumCircuit(5)
# Quantum Instantaneous Polynomial Time example
circuit.cx(0, 1)
circuit.cx(2, 1)
circuit.cx(4, 3)
circuit.cx(2, 3) 
circuit.z(0)
circuit.z(4)
circuit.cx(0, 1)
circuit.cx(2, 1)
circuit.cx(4, 3)
circuit.cx(2, 3) 
circuit.cx(3, 2) 

print(circuit)

pm = PassManager()
pm.append([CommutationAnalysis(), CommutativeCancellation()])
new_circuit=pm.run(circuit)
print(new_circuit)

ghz.py

# -*- coding: utf-8 -*-

# This code is part of Qiskit.
#
# (C) Copyright IBM 2017.
#
# This code is licensed under the Apache License, Version 2.0. You may
# obtain a copy of this license in the LICENSE.txt file in the root directory
# of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
#
# Any modifications or derivative works of this code must retain this
# copyright notice, and modified files need to carry a notice indicating
# that they have been altered from the originals.

"""
GHZ state example. It also compares running on experiment and simulator.
"""

from qiskit import QuantumCircuit
from qiskit import BasicAer, execute


###############################################################
# Make a quantum circuit for the GHZ state.
###############################################################
num_qubits = 5
qc = QuantumCircuit(num_qubits, num_qubits, name='ghz')

# Create a GHZ state
qc.h(0)
for i in range(num_qubits-1):
    qc.cx(i, i+1)
# Insert a barrier before measurement
qc.barrier()
# Measure all of the qubits in the standard basis
for i in range(num_qubits):
    qc.measure(i, i)

sim_backend = BasicAer.get_backend('qasm_simulator')
job = execute(qc, sim_backend, shots=1024)
result = job.result()
print('Qasm simulator : ')
print(result.get_counts(qc))

initialize.py

# -*- coding: utf-8 -*-

# This code is part of Qiskit.
#
# (C) Copyright IBM 2017.
#
# This code is licensed under the Apache License, Version 2.0. You may
# obtain a copy of this license in the LICENSE.txt file in the root directory
# of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
#
# Any modifications or derivative works of this code must retain this
# copyright notice, and modified files need to carry a notice indicating
# that they have been altered from the originals.

"""
Example use of the initialize gate to prepare arbitrary pure states.
"""

import math
from qiskit import QuantumCircuit, execute, BasicAer


###############################################################
# Make a quantum circuit for state initialization.
###############################################################
circuit = QuantumCircuit(4, 4, name="initializer_circ")

desired_vector = [
    1 / math.sqrt(4) * complex(0, 1),
    1 / math.sqrt(8) * complex(1, 0),
    0,
    0,
    0,
    0,
    0,
    0,
    1 / math.sqrt(8) * complex(1, 0),
    1 / math.sqrt(8) * complex(0, 1),
    0,
    0,
    0,
    0,
    1 / math.sqrt(4) * complex(1, 0),
    1 / math.sqrt(8) * complex(1, 0)]

circuit.initialize(desired_vector, [0, 1, 2, 3])

circuit.measure([0, 1, 2, 3], [0, 1, 2, 3])

print(circuit)

###############################################################
# Execute on a simulator backend.
###############################################################
shots = 10000

# Desired vector
print("Desired probabilities: ")
print(str(list(map(lambda x: format(abs(x * x), '.3f'), desired_vector))))

# Initialize on local simulator
sim_backend = BasicAer.get_backend('qasm_simulator')
job = execute(circuit, sim_backend, shots=shots)
result = job.result()

counts = result.get_counts(circuit)

qubit_strings = [format(i, '0%sb' % 4) for
                 i in range(2 ** 4)]
print("Probabilities from simulator: ")
print([format(counts.get(s, 0) / shots, '.3f') for
       s in qubit_strings])

load_qasm.py

# -*- coding: utf-8 -*-

# This code is part of Qiskit.
#
# (C) Copyright IBM 2017, 2018.
#
# This code is licensed under the Apache License, Version 2.0. You may
# obtain a copy of this license in the LICENSE.txt file in the root directory
# of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
#
# Any modifications or derivative works of this code must retain this
# copyright notice, and modified files need to carry a notice indicating
# that they have been altered from the originals.

"""Example on how to load a file into a QuantumCircuit."""

from qiskit import QuantumCircuit
from qiskit import QiskitError, execute, BasicAer

circ = QuantumCircuit.from_qasm_file("examples/qasm/entangled_registers.qasm")
print(circ)

# See the backend
sim_backend = BasicAer.get_backend('qasm_simulator')


# Compile and run the Quantum circuit on a local simulator backend
job_sim = execute(circ, sim_backend)
sim_result = job_sim.result()

# Show the results
print("simulation: ", sim_result)
print(sim_result.get_counts(circ))

qft.py

# -*- coding: utf-8 -*-

# This code is part of Qiskit.
#
# (C) Copyright IBM 2017.
#
# This code is licensed under the Apache License, Version 2.0. You may
# obtain a copy of this license in the LICENSE.txt file in the root directory
# of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
#
# Any modifications or derivative works of this code must retain this
# copyright notice, and modified files need to carry a notice indicating
# that they have been altered from the originals.

"""
Quantum Fourier Transform examples.
"""

import math
from qiskit import QuantumCircuit
from qiskit import execute, BasicAer


###############################################################
# make the qft
###############################################################
def input_state(circ, n):
    """n-qubit input state for QFT that produces output 1."""
    for j in range(n):
        circ.h(j)
        circ.u1(-math.pi/float(2**(j)), j)

def qft(circ, n):
    """n-qubit QFT on q in circ."""
    for j in range(n):
        for k in range(j):
            circ.cu1(math.pi/float(2**(j-k)), j, k)
        circ.h(j)

qft3 = QuantumCircuit(5, 5, name="qft3")
qft4 = QuantumCircuit(5, 5, name="qft4")
qft5 = QuantumCircuit(5, 5, name="qft5")

input_state(qft3, 3)
qft3.barrier()
qft(qft3, 3)
qft3.barrier()
for j in range(3):
    qft3.measure(j, j)

input_state(qft4, 4)
qft4.barrier()
qft(qft4, 4)
qft4.barrier()
for j in range(4):
    qft4.measure(j, j)

input_state(qft5, 5)
qft5.barrier()
qft(qft5, 5)
qft5.barrier()
for j in range(5):
    qft5.measure(j, j)

print(qft3)
print(qft4)
print(qft5)

print('Qasm simulator')
sim_backend = BasicAer.get_backend('qasm_simulator')
job = execute([qft3, qft4, qft5], sim_backend, shots=1024)
result = job.result()
print(result.get_counts(qft3))
print(result.get_counts(qft4))
print(result.get_counts(qft5))

rippleadd.py

# -*- coding: utf-8 -*-

# This code is part of Qiskit.
#
# (C) Copyright IBM 2017.
#
# This code is licensed under the Apache License, Version 2.0. You may
# obtain a copy of this license in the LICENSE.txt file in the root directory
# of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
#
# Any modifications or derivative works of this code must retain this
# copyright notice, and modified files need to carry a notice indicating
# that they have been altered from the originals.

"""
Ripple adder example based on Cuccaro et al., quant-ph/0410184.

"""

from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit
from qiskit import BasicAer
from qiskit import execute

###############################################################
# Set the backend name and coupling map.
###############################################################
backend = BasicAer.get_backend("qasm_simulator")
coupling_map = [[0,1], [0, 8], [1, 2], [1, 9], [2, 3], [2, 10], [3, 4], [3, 11],
                [4, 5], [4, 12], [5, 6], [5, 13], [6, 7], [6, 14], [7, 15], [8, 9],
                [9, 10], [10, 11], [11, 12], [12, 13], [13, 14], [14, 15]]

###############################################################
# Make a quantum program for the n-bit ripple adder.
###############################################################
n = 2

a = QuantumRegister(n, "a")
b = QuantumRegister(n, "b")
cin = QuantumRegister(1, "cin")
cout = QuantumRegister(1, "cout")
ans = ClassicalRegister(n+1, "ans")
qc = QuantumCircuit(a, b, cin, cout, ans, name="rippleadd")


def majority(p, a, b, c):
    """Majority gate."""
    p.cx(c, b)
    p.cx(c, a)
    p.ccx(a, b, c)


def unmajority(p, a, b, c):
    """Unmajority gate."""
    p.ccx(a, b, c)
    p.cx(c, a)
    p.cx(a, b)


# Build a temporary subcircuit that adds a to b,
# storing the result in b
adder_subcircuit = QuantumCircuit(cin, a, b, cout)
majority(adder_subcircuit, cin[0], b[0], a[0])
for j in range(n - 1):
    majority(adder_subcircuit, a[j], b[j + 1], a[j + 1])
adder_subcircuit.cx(a[n - 1], cout[0])
for j in reversed(range(n - 1)):
    unmajority(adder_subcircuit, a[j], b[j + 1], a[j + 1])
unmajority(adder_subcircuit, cin[0], b[0], a[0])

# Set the inputs to the adder
qc.x(a[0])  # Set input a = 0...0001
qc.x(b)   # Set input b = 1...1111
# Apply the adder
qc += adder_subcircuit
# Measure the output register in the computational basis
for j in range(n):
    qc.measure(b[j], ans[j])
qc.measure(cout[0], ans[n])

###############################################################
# execute the program.
###############################################################

# First version: not mapped
job = execute(qc, backend=backend, coupling_map=None, shots=1024)
result = job.result()
print(result.get_counts(qc))

# Second version: mapped to 2x8 array coupling graph
job = execute(qc, backend=backend, coupling_map=coupling_map, shots=1024)
result = job.result()
print(result.get_counts(qc))

# Both versions should give the same distribution

stochastic_swap.py

# -*- coding: utf-8 -*-

# This code is part of Qiskit.
#
# (C) Copyright IBM 2017, 2019.
#
# This code is licensed under the Apache License, Version 2.0. You may
# obtain a copy of this license in the LICENSE.txt file in the root directory
# of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
#
# Any modifications or derivative works of this code must retain this
# copyright notice, and modified files need to carry a notice indicating
# that they have been altered from the originals.

"""Example of using the StochasticSwap pass."""

from qiskit.transpiler.passes import StochasticSwap
from qiskit.transpiler import CouplingMap, Layout
from qiskit.converters import circuit_to_dag, dag_to_circuit
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit

coupling = CouplingMap([[0, 1], [1, 2], [1, 3]])
qr = QuantumRegister(4, 'q')
cr = ClassicalRegister(4, 'c')
circ = QuantumCircuit(qr, cr)
circ.cx(qr[1], qr[2])
circ.cx(qr[0], qr[3])
circ.measure(qr[0], cr[0])
circ.h(qr)
circ.cx(qr[0], qr[1])
circ.cx(qr[2], qr[3])
circ.measure(qr[0], cr[0])
circ.measure(qr[1], cr[1])
circ.measure(qr[2], cr[2])
circ.measure(qr[3], cr[3])
dag = circuit_to_dag(circ)
#                                             ┌─┐┌───┐        ┌─┐
# q_0: |0>─────────────────■──────────────────┤M├┤ H ├──■─────┤M├
#                   ┌───┐  │                  └╥┘└───┘┌─┴─┐┌─┐└╥┘
# q_1: |0>──■───────┤ H ├──┼───────────────────╫──────┤ X ├┤M├─╫─
#         ┌─┴─┐┌───┐└───┘  │               ┌─┐ ║      └───┘└╥┘ ║
# q_2: |0>┤ X ├┤ H ├───────┼─────────■─────┤M├─╫────────────╫──╫─
#         └───┘└───┘     ┌─┴─┐┌───┐┌─┴─┐┌─┐└╥┘ ║            ║  ║
# q_3: |0>───────────────┤ X ├┤ H ├┤ X ├┤M├─╫──╫────────────╫──╫─
#                        └───┘└───┘└───┘└╥┘ ║  ║            ║  ║
#  c_0: 0 ═══════════════════════════════╬══╬══╩════════════╬══╩═
#                                        ║  ║               ║
#  c_1: 0 ═══════════════════════════════╬══╬═══════════════╩════
#                                        ║  ║
#  c_2: 0 ═══════════════════════════════╬══╩════════════════════
#                                        ║
#  c_3: 0 ═══════════════════════════════╩═══════════════════════
#
#                                ┌─┐┌───┐                     ┌─┐
# q_0: |0>────────────────────■──┤M├┤ H ├──────────────────■──┤M├──────
#                           ┌─┴─┐└╥┘└───┘┌───┐┌───┐      ┌─┴─┐└╥┘┌─┐
# q_1: |0>──■───X───────────┤ X ├─╫──────┤ H ├┤ X ├─X────┤ X ├─╫─┤M├───
#         ┌─┴─┐ │      ┌───┐└───┘ ║      └───┘└─┬─┘ │    └───┘ ║ └╥┘┌─┐
# q_2: |0>┤ X ├─┼──────┤ H ├──────╫─────────────■───┼──────────╫──╫─┤M├
#         └───┘ │ ┌───┐└───┘      ║                 │ ┌─┐      ║  ║ └╥┘
# q_3: |0>──────X─┤ H ├───────────╫─────────────────X─┤M├──────╫──╫──╫─
#                 └───┘           ║                   └╥┘      ║  ║  ║
#  c_0: 0 ════════════════════════╩════════════════════╬═══════╩══╬══╬═
#                                                      ║          ║  ║
#  c_1: 0 ═════════════════════════════════════════════╬══════════╩══╬═
#                                                      ║             ║
#  c_2: 0 ═════════════════════════════════════════════╬═════════════╩═
#                                                      ║
#  c_3: 0 ═════════════════════════════════════════════╩═══════════════
#
#
#     2
#     |
# 0 - 1 - 3
# Build the expected output to verify the pass worked
expected = QuantumCircuit(qr, cr)
expected.cx(qr[1], qr[2])
expected.swap(qr[0], qr[1])
expected.cx(qr[1], qr[3])
expected.h(qr[3])
expected.h(qr[2])
expected.measure(qr[1], cr[0])
expected.h(qr[0])
expected.swap(qr[1], qr[3])
expected.h(qr[3])
expected.cx(qr[2], qr[1])
expected.measure(qr[2], cr[2])
expected.swap(qr[1], qr[3])
expected.measure(qr[3], cr[3])
expected.cx(qr[1], qr[0])
expected.measure(qr[1], cr[0])
expected.measure(qr[0], cr[1])
expected_dag = circuit_to_dag(expected)

# Run the pass on the dag from the input circuit
pass_ = StochasticSwap(coupling, 20, 13)
after = pass_.run(dag)
# Verify the output of the pass matches our expectation
assert expected_dag == after

using_qiskit_terra_level_0.py

# -*- coding: utf-8 -*-

# This code is part of Qiskit.
#
# (C) Copyright IBM 2017, 2018.
#
# This code is licensed under the Apache License, Version 2.0. You may
# obtain a copy of this license in the LICENSE.txt file in the root directory
# of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
#
# Any modifications or derivative works of this code must retain this
# copyright notice, and modified files need to carry a notice indicating
# that they have been altered from the originals.

"""
Example showing how to use Qiskit-Terra at level 0 (novice).

This example shows the most basic way to user Terra. It builds some circuits
and runs them on both the BasicAer (local Qiskit provider) or IBMQ (remote IBMQ provider).

To control the compile parameters we have provided a transpile function which can be used 
as a level 1 user.

"""

import time

# Import the Qiskit modules
from qiskit import QuantumCircuit, QiskitError
from qiskit import execute, BasicAer

# making first circuit: bell state
qc1 = QuantumCircuit(2, 2)
qc1.h(0)
qc1.cx(0, 1)
qc1.measure([0,1], [0,1])

# making another circuit: superpositions
qc2 = QuantumCircuit(2, 2)
qc2.h([0,1])
qc2.measure([0,1], [0,1])

# setting up the backend
print("(BasicAER Backends)")
print(BasicAer.backends())

# running the job
job_sim = execute([qc1, qc2], BasicAer.get_backend('qasm_simulator'))
sim_result = job_sim.result()

# Show the results
print(sim_result.get_counts(qc1))
print(sim_result.get_counts(qc2))