二次型矩阵

二次型的每一项都是二次的，如果是平方则是平方项，如果是两个不同的变量则为交叉项。二次型如：$x^2+xy+y^2$。

二次型->矩阵表达式
例：$x_1^2+2x_1{x}_2+x_2^2-x_2{x}_3+2x_3^2-2x_1{x}_3$
解：

1. 平方项的系数直接做成主对角线的元素
2. 交叉项的系数除以2放到两个对称的相应位置
   

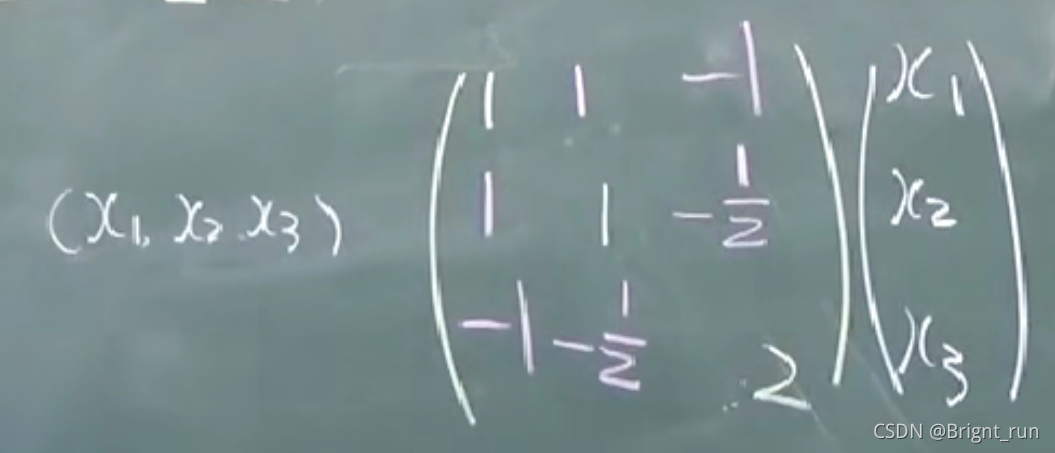
上图可表示为 $X^{T}AX$，$A$ 为二次型的矩阵，$A$ 的秩为二次型的秩，因此二次型的矩阵一定是对称的，即 $A^T=A$。

标准型
只有平方项，如$d_1{y}_1^2+d_2{y}_2^2+...+d_n{y}_n^2$，$d_i$ 可以是任意数。

线性替换
假设二次型 $f(x)=X^{T}AX$，令 $X=CY$(线性替换)，可得
$$f(x)=X^{T}AX=(CY{)}^{T}A(CY)=Y^T(C^{T}AC)Y$$
令 $B=C^{T}AC$，由于标准型只有平方项，所以其只有主对角线元素，因此换做 $Y$ 为自变量时 $f(Y)$ 为标准型，同时 $B$ 为新二次型矩阵。

若$|C|\ne 0$，则该替换为可逆替换或者非退化或者非奇异替换。