题目描述
有一个 m × n 的矩形岛屿,与 太平洋 和 大西洋 相邻。 “太平洋” 处于大陆的左边界和上边界,而 “大西洋” 处于大陆的右边界和下边界。
这个岛被分割成一个由若干方形单元格组成的网格。给定一个 m x n 的整数矩阵 heights , heights[r][c] 表示坐标 (r, c) 上单元格 高于海平面的高度 。
岛上雨水较多,如果相邻单元格的高度 小于或等于 当前单元格的高度,雨水可以直接向北、南、东、西流向相邻单元格。水可以从海洋附近的任何单元格流入海洋。
返回网格坐标 result 的 2D 列表 ,其中 result[i] = [ri, ci] 表示雨水从单元格 (ri, ci) 流动 既可流向太平洋也可流向大西洋 。
示例 1
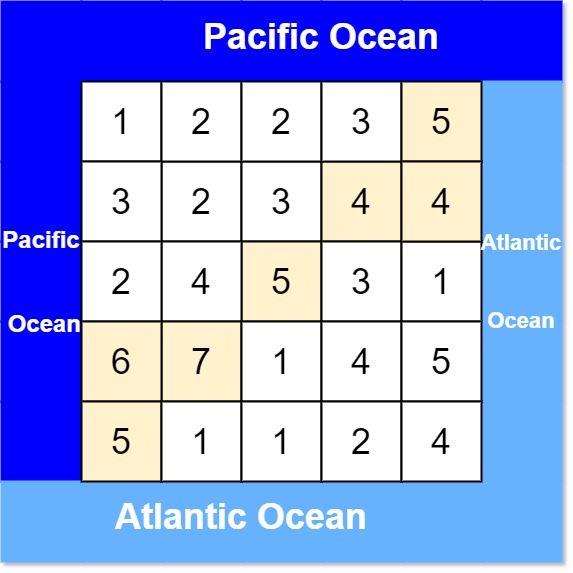
输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]
示例 2:
输入: heights = [[2,1],[1,2]]
输出: [[0,0],[0,1],[1,0],[1,1]]
提示:
m == heights.lengthn == heights[r].length1 <= m, n <= 2000 <= heights[r][c] <= 10^5
解题思路
这道题的核心是判断每个单元格的雨水是否能流向两个海洋。由于水从高向低流(或等高),如果从每个单元格正向模拟流动,会导致时间复杂度过高(O(m*n * m*n))。因此,我们采用逆向思维:从海洋开始逆向流动,标记能到达的单元格。
题目理解
-
水流方向:水从高处流向低处或等高处(高度小于等于当前位置)
-
边界定义:
-
太平洋:左边界(第0列)和上边界(第0行)
-
大西洋:右边界(第n-1列)和下边界(第m-1行)
-
-
目标:找到既能流到太平洋又能流到大西洋的所有位置
逆向思维
正向思考:从每个位置出发,判断能否同时到达两个海洋(复杂度高)
逆向思考:从海洋边界出发,找到所有能从海洋"逆流而上"到达的位置
-
从太平洋边界开始,找所有太平洋能到达的位置
-
从大西洋边界开始,找所有大西洋能到达的位置
-
两个集合的交集就是答案
逆流规则
由于是逆向思考,逆流的条件是:当前位置的高度 >= 相邻位置的高度
方法一:深度优先搜索(DFS)
-
创建两个二维布尔数组,分别记录太平洋和大西洋能到达的位置
-
从太平洋边界的所有位置开始DFS,标记所有能到达的位置
-
从大西洋边界的所有位置开始DFS,标记所有能到达的位置
-
遍历整个网格,找到同时被两个数组标记为true的位置
方法二:广度优先搜索(BFS)
使用队列替代递归,逐层扩展搜索范围,原理与DFS相同。
算法图解
以示例1为例:heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
原始矩阵:
1 2 2 3 5
3 2 3 4 4
2 4 5 3 1
6 7 1 4 5
5 1 1 2 4
太平洋边界:第0行 + 第0列
大西洋边界:最后一行 + 最后一列
第一步:从太平洋边界开始DFS
太平洋可达(P标记):
P P P P P
P P P P P
P P P P -
P P - P -
P - - - -
第二步:从大西洋边界开始DFS
大西洋可达(A标记):
- - - - A
- - - A A
- - A A A
A A - A A
A - - - A
第三步:找交集(既有P又有A)
交集位置:
- - - - ✓
- - - ✓ ✓
- - ✓ - -
✓ ✓ - - -
✓ - - - -
对应坐标:[[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]
详细代码实现
Java 实现 - DFS 方法
import java.util.*;
/**
* 417. 太平洋大西洋水流问题
* DFS
*/
class Solution {
// 四个方向:上、下、左、右
int[][] directions = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
int m,n;
public List<List<Integer>> pacificAtlantic(int[][] heights) {
List<List<Integer>> res = new ArrayList<>();
if(heights==null||heights.length==0||heights[0].length==0)
return res;
m = heights.length;
n = heights[0].length;
// 记录太平洋和大西洋能到达的位置
boolean[][] pacific = new boolean[m][n];
boolean[][] atlantic = new boolean[m][n];
// 从太平洋边界开始DFS(左边界和上边界)
for(int i=0;i<m;i++){
dfs(heights,pacific,i,0); // 左边界
}
for(int j=0;j<n;j++){
dfs(heights,pacific,0,j); // 上边界
}
// 从大西洋边界开始DFS(右边界和下边界)
for(int i=0;i<m;i++){
dfs(heights,atlantic,i,n-1); // 右边界
}
for(int j=0;j<n;j++){
dfs(heights,atlantic,m-1,j); // 下边界
}
// 找到同时能到达两个海洋的位置
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(pacific[i][j]&&atlantic[i][j]){
List<Integer> list = new ArrayList<>();
list.add(i);
list.add(j);
res.add(list);
}
}
}
return res;
}
void dfs(int[][] heights,boolean[][] visited,int row,int col){
// 标记当前位置为可达
visited[row][col] = true;
// 向四个方向探索
for(int[] dir:directions){
int newRow = row + dir[0];
int newCol = col + dir[1];
// 检查下一个位置是否合法以及是否满足流动条件
// 边界检查、是否已访问检查、高度条件检查
if (newRow < 0 || newRow >= m || newCol < 0 || newCol >= n ||
visited[newRow][newCol] ||
heights[newRow][newCol] < heights[row][col])
continue;
dfs(heights, visited, newRow, newCol);
}
}
}
Java 实现 - BFS 方法
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
/**
* 417. 太平洋大西洋水流问题
* BFS
*/
class Solution {
int[][] directions = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
int m, n;
public List<List<Integer>> pacificAtlantic(int[][] heights) {
List<List<Integer>> res = new ArrayList<>();
if (heights == null || heights.length == 0 || heights[0].length == 0)
return res;
m = heights.length;
n = heights[0].length;
// 记录太平洋和大西洋能到达的位置
boolean[][] pacific = new boolean[m][n];
boolean[][] atlantic = new boolean[m][n];
// 创建队列用于BFS
Queue<int[]> pacificQueue = new LinkedList<>();
Queue<int[]> atlanticQueue = new LinkedList<>();
// 初始化边界点
for (int i = 0; i < m; i++) {
// 太平洋:左边界
pacificQueue.offer(new int[]{i, 0});
pacific[i][0] = true;
// 大西洋:右边界
atlanticQueue.offer(new int[]{i, n - 1});
atlantic[i][n - 1] = true;
}
for (int j = 0; j < n; j++) {
// 太平洋:上边界
pacificQueue.offer(new int[]{0, j});
pacific[0][j] = true;
// 大西洋:下边界
atlanticQueue.offer(new int[]{m - 1, j});
atlantic[m - 1][j] = true;
}
// 分别进行BFS
bfs(heights, pacific, pacificQueue);
bfs(heights, atlantic, atlanticQueue);
// 找到同时能到达两个海洋的位置
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (pacific[i][j] && atlantic[i][j]) {
List<Integer> list = new ArrayList<>();
list.add(i);
list.add(j);
res.add(list);
}
}
}
return res;
}
void bfs(int[][] heights, boolean[][] visited, Queue<int[]> queue) {
while (!queue.isEmpty()) {
int[] cur = queue.poll();
int row = cur[0];
int col = cur[1];
// 向四个方向探索
for (int[] dir : directions) {
int newRow = row + dir[0];
int newCol = col + dir[1];
// 检查下一个位置是否合法以及是否满足流动条件
// 边界检查、是否已访问检查、高度条件检查
if (newRow < 0 || newRow >= m || newCol < 0 || newCol >= n ||
visited[newRow][newCol] ||
heights[newRow][newCol] < heights[row][col])
continue;
visited[newRow][newCol] = true;
queue.offer(new int[]{newRow, newCol});
}
}
}
}
C# 实现 - DFS 方法
public class Solution
{
// 四个方向:上、下、左、右
int[][] dirs = new[] { [-1, 0], new[] { 1, 0 }, new[] { 0, -1 }, new[] { 0, 1 } };
private int m, n;
public IList<IList<int>> PacificAtlantic(int[][] heights)
{
IList<IList<int>> res = new List<IList<int>>();
if (heights == null || heights.Length == 0 || heights[0].Length == 0)
{
return res;
}
m = heights.Length;
n = heights[0].Length;
bool[,] pacific = new bool[m, n];
bool[,] atlantic = new bool[m, n];
// 从太平洋边界开始DFS(左边界和上边界)
for (int i = 0; i < m; i++)
{
dfs(heights, pacific, i, 0); // 左边界
}
for (int j = 0; j < n; j++)
{
dfs(heights, pacific, 0, j); // 上边界
}
// 从大西洋边界开始DFS(右边界和下边界)
for (int i = 0; i < m; i++)
{
dfs(heights, atlantic, i, n - 1); // 右边界
}
for (int j = 0; j < n; j++)
{
dfs(heights, atlantic, m - 1, j); // 下边界
}
// 找到同时能到达两个海洋的位置
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n; j++)
{
if (pacific[i, j] && atlantic[i, j])
{
res.Add(new List<int> { i, j });
}
}
}
return res;
}
void dfs(int[][] heights, bool[,] visited, int row, int col)
{
visited[row, col] = true;
foreach (var dir in dirs)
{
int newRow = row + dir[0];
int newCol = col + dir[1];
if (newRow < 0 || newRow >= m || newCol < 0 || newCol >= n ||
visited[newRow, newCol] || heights[newRow][newCol] < heights[row][col])
{
continue;
}
dfs(heights, visited, newRow, newCol);
}
}
}
C# 实现 - BFS 方法
public class Solution {
// 四个方向:上、下、左、右
private int[][] dirs = new int[][]{new int[]{-1, 0}, new int[]{1, 0}, new int[]{0, -1}, new int[]{0, 1}};
private int m, n;
public IList<IList<int>> PacificAtlantic(int[][] heights) {
IList<IList<int>> res = new List<IList<int>>();
if (heights == null || heights.Length == 0 || heights[0].Length == 0) {
return res;
}
m = heights.Length;
n = heights[0].Length;
// 记录太平洋和大西洋能到达的位置
bool[,] pacific = new bool[m, n];
bool[,] atlantic = new bool[m, n];
Queue<int[]> pacificQueue = new Queue<int[]>();
Queue<int[]> atlanticQueue = new Queue<int[]>();
// 初始化边界点
for (int i = 0; i < m; i++)
{
// 太平洋:左边界
pacific[i, 0] = true;
pacificQueue.Enqueue(new int[]{i, 0});
// 大西洋:右边界
atlantic[i, n - 1] = true;
atlanticQueue.Enqueue(new int[]{i, n - 1});
}
for (int j = 0; j < n; j++)
{
// 太平洋:上边界
pacific[0, j] = true;
pacificQueue.Enqueue(new int[]{0, j});
// 大西洋:下边界
atlantic[m - 1, j] = true;
atlanticQueue.Enqueue(new int[]{m - 1, j});
}
// 分别进行BFS
Bfs(heights, pacific, pacificQueue);
Bfs(heights, atlantic, atlanticQueue);
// 找到同时能到达两个海洋的位置
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n; j++)
{
if (pacific[i, j] && atlantic[i, j])
{
res.Add(new List<int>{i, j});
}
}
}
return res;
}
void Bfs(int[][] heights, bool [,] visited, Queue<int[]> queue)
{
while (queue.Count>0)
{
int[] cur = queue.Dequeue();
int row = cur[0];
int col = cur[1];
// 向四个方向探索
foreach (var dir in dirs)
{
int newRow = row + dir[0];
int newCol = col + dir[1];
if (newRow < 0 || newRow >= m || newCol < 0 || newCol >= n ||
visited[newRow, newCol] || heights[newRow][newCol] < heights[row][col])
continue;
visited[newRow, newCol] = true;
queue.Enqueue(new int[]{newRow, newCol});
}
}
}
}
复杂度分析
时间复杂度
-
DFS/BFS方法:O(m × n)
-
每个格子最多被访问两次(分别从两个海洋边界)
-
总体遍历复杂度为线性
-
空间复杂度
-
DFS方法:O(m × n)
-
两个二维布尔数组:O(2 × m × n)
-
递归调用栈:最坏情况O(m × n)
-
-
BFS方法:O(m × n)
-
两个二维布尔数组:O(2 × m × n)
-
队列空间:最坏情况O(m × n)
-





















 183
183

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








