【Datawhale之Happy-LLM】Github最火大模型原理与实践教程task03精华~我不相信看完你还不知道什么是Transformer的注意力机制

Task03-05：第二章 Transformer架构

本篇是task03： 2.1 注意力机制
（这是笔者自己的学习记录，仅供参考，原始学习链接，愿 LLM 越来越好❤）

Transformer架构很重要，需要分几天啃一啃。

---

在NLP中的核心基础任务文本表示，从用统计方法得到向量进入用神经网络方法。而这个神经网络NN（Neural Network）确实从CV计算机视觉发展来的。

所以我们应该先了解一下CV中神经网络的核心架构。

---

一、CV中NN的核心架构（共3种）

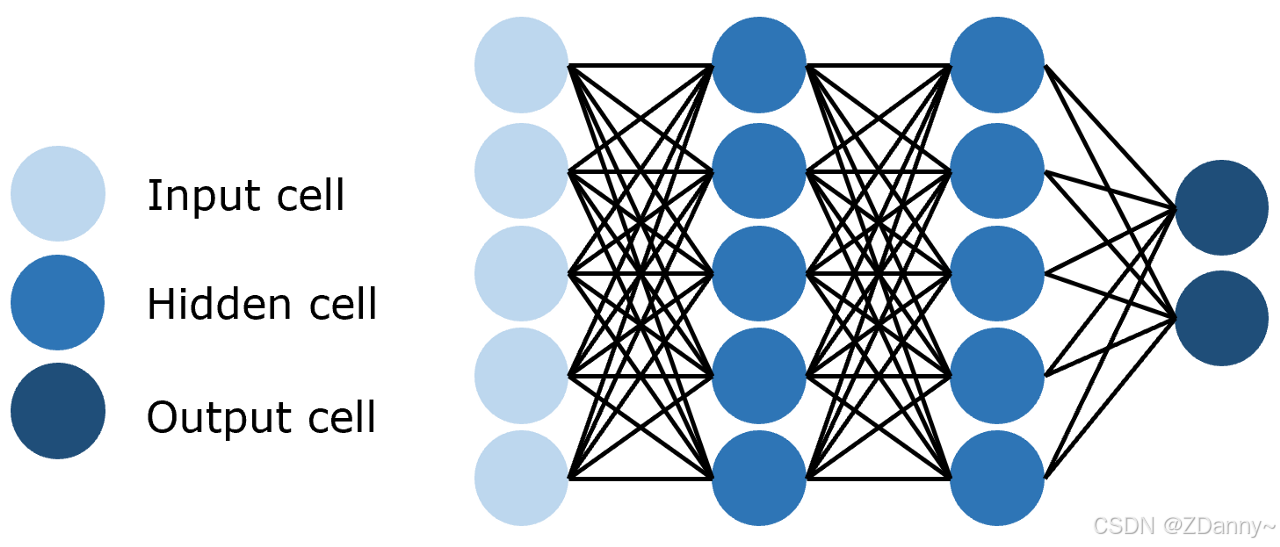
1、FNN（全连接 Feedforward NN）：

• 连接方式：每一层的每个神经元都和上下的每个神经元连接。

• 参数量：全连接层的参数量 = 输入维度 × 输出维度，6层的网络，要计算6-1次相加

• 特点：简单但是参数量巨大

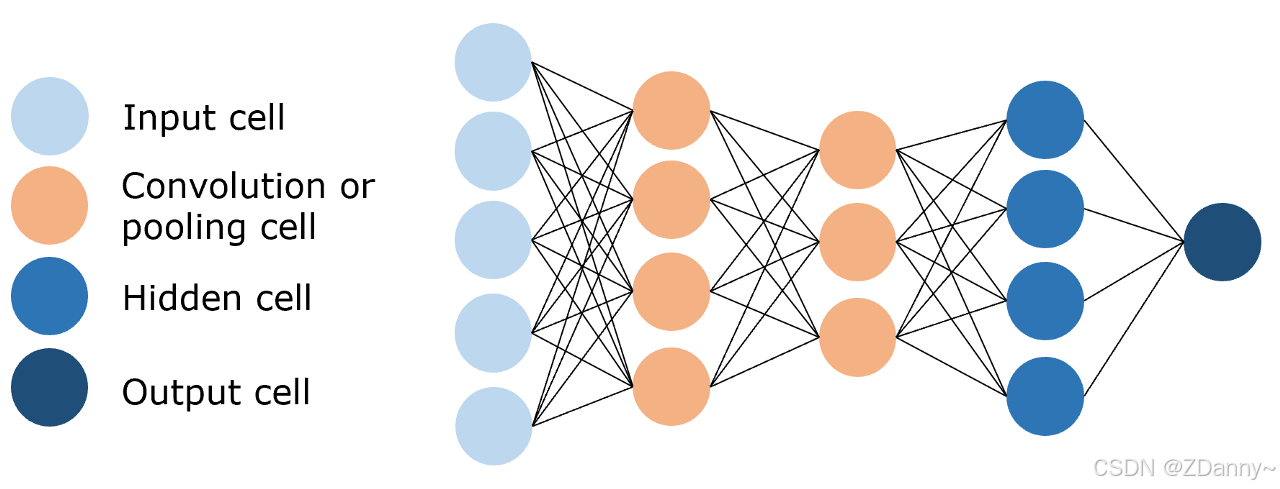
2、CNN（卷积 Convolutional NN）：

• 连接方式：卷积核
• 参数量：3x3（卷积核）x 输入通道数 x 输出通道数
• 特点：参数量远小于FNN的，进行特征提取和学习

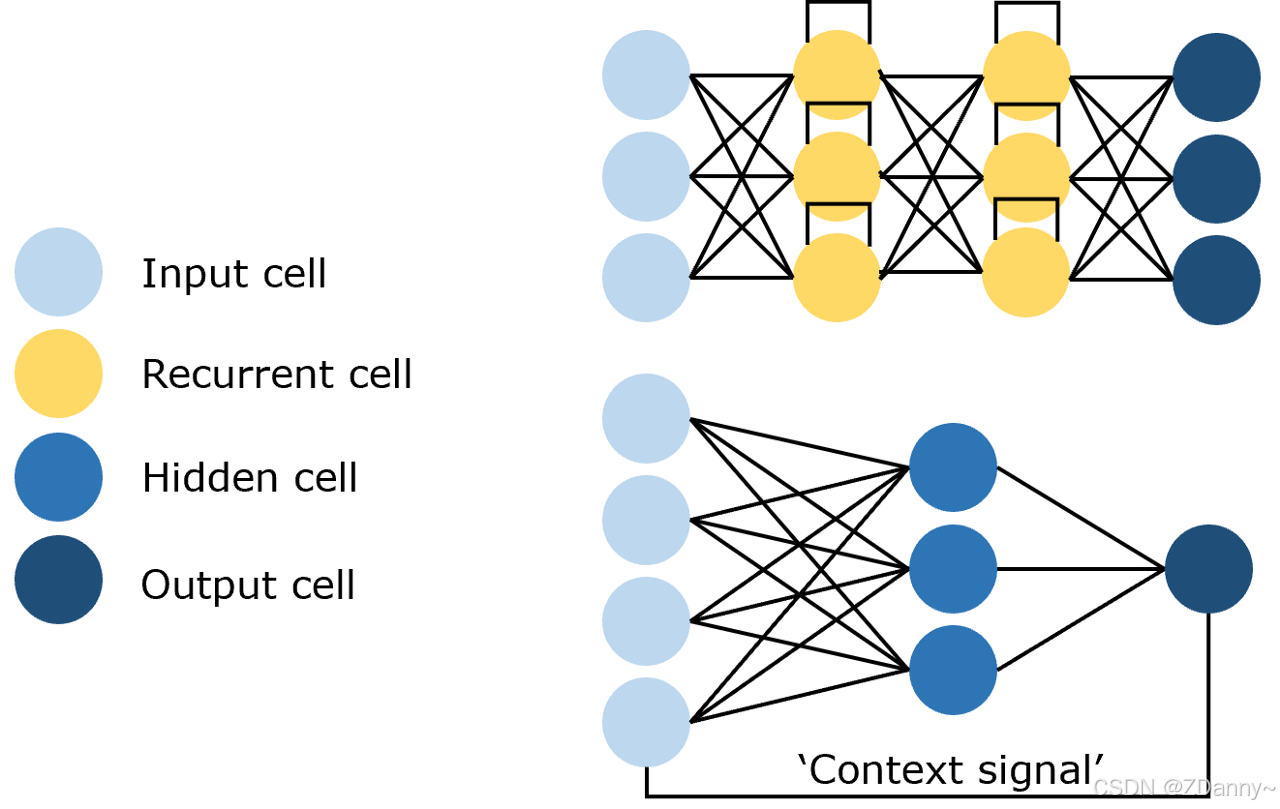
3、RNN（循环 Recycle NN）：

• 有循环，输出作为输入

---

二、NN在NLP的使用发展

1、RNN、LSTM架构

以前用的比较多（LSTM是RNN的衍生，如ELMo文本表示模型用的双向LSTM）NLP处理的是文本序列，用这种架构效果比其他2种好。

这种架构的优点？

能捕捉时序信息、适合序列生成

架构的问题？

2个
一个是串行不能并行计算，时间久。
另一个是RNN长距离关系很难捕捉，且要把整个序列读到内存，对序列长度有限制

2、Transformer架构

现在火起来的，架构中的核心是Attention注意力机制（这个机制常被融到RNN中，现在被单拎出来做成新的NN架构，并用在NLP作为LLM的核心架构了）也是深度学习里最核心的架构。

总结：架构核心是CV领域RNN的Attention机制，是神经网络、深度学习的架构，现用在NLP的LLM中

Attention注意力机制的思想是什么？

cv领域的思想是看图片只要关注重点部分（比如看海边画你不用每个细节注意到，你只要看天颜色美你就觉得画好看）；
nlp领域的思想是语言只要关注重点token进行计算（人的语言理解也是，听别人说话可能你听些词就能自动脑补别人全部意思了）

---

三、注意力机制公式推导

attention的核心计算公式是什么？

$$attention(Q,K,V)=softmax（\frac{Q{K}^T}{\sqrt{d_k}}）V.$$

1、核心变量

Q（query查询值）、K（key键）、V（value值）

【大写为矩阵，小写为向量。tt = tokens target ，ts = tokens source】

• q词向量 =（1 x d_k）
• Q矩阵 = （目标序列token数 n_tt x d_k）
• K矩阵 = （源序列token数 n_ts x d_k）
• V矩阵 = （源序列token数 n_ts x d_v）

备注：K和V都来自同一个输入序列，行数是一样的。k和v都来自同一个token，但是数值却不同。（因为token进行embedding后会有一个x向量，会分别乘不同的权重矩阵进行线性变换。k
= xW_k，v=xW_v。）

（多头注意力中，当d_model=512，head=8时）
$$d_k=d_v=\frac{d_{model}}{h}=\frac{512}{8}=64$$
（自注意力中，QKV来自同一个序列，每个token对应一行）
$$n_{tt}=n_{ts}$$

---

2、公式拆解

拆解式子1——得到权重：

单个token（“fruit”）和序列每个token（“apple”、“banana”，“car”）的相似度【点积】
$$x=q{K}^{\mathsf{T}}维度(1\times n_{ts})$$维度变化如下：$$q\in {\mathbb{R}}^{1\times d_k},K\in {\mathbb{R}}^{n_{ts}\times d_k}$$$$(1\times d_k)\cdot (n_{tt}\times d_k{)}^{\mathsf{T}}=(1\times d_k)\cdot (d_k\times n_{ts})=(1\times n_{ts})$$结果值含义如下：
$$q_{fruit}=\left[\begin{array}{cccc}1.0& 0.5& -0.3& 0.8\end{array}\right],$$$$K=[$$