拓扑排序算法和关键路径算法

原创已于 2025-06-17 21:21:33 修改 · 331 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#排序算法 #算法 #数据结构

于 2025-06-17 16:41:12 首次发布

1、拓扑算法

（1）AOV网（Activity On Vertex Network):表示工程的有向图中用顶点表示活动，用弧表示活动之间的优先顺序的网。

（2）拓扑排序：拓扑排序是对有向无环图 (DAG) 的顶点进行排序的算法，使得对于每一条有向边 (u,v)，顶点 u 在排序中都出现在顶点 v 之前。

（3） 检测是否有环：如果网的顶点全部被输出则说明不存在回路，否则存在回路。

算法实现：

代码及注释如下：

#include<iostream>
#include<vector>
#include<list>
#include<queue>
using namespace std;
                //该算法比较适合使用邻接表构造图 
struct vertex{
	int in=0;//这里添加一个int表示入度 
	char vexc;//表示顶点字符 
	list<int>vexl;//表示与顶点相连通的点在顶点数组中的坐标 
};
struct LGraph{   //LGraph表示邻接表构成的图(list) 
	vector<vertex>vex;
	vector<int>topo;//拓扑排序序列
	LGraph(int n){
		vex.resize(n);		
	}
}; 
int findPos(LGraph lg,char vn){
	int n=lg.vex.size();
	int i;
	for(i=0;i<n;i++){
		if(lg.vex[i].vexc==vn)
		    return i;
	}
	return -1;
}
void creatLGraph(LGraph& lg,int n,int k){
	int i;
	for(i=0;i<n;i++){
		cin>>lg.vex[i].vexc;
	}
	for(i=0;i<k;i++){
		char v1,v2;
		cin>>v1>>v2;
		int M=findPos(lg,v1);
		int N=findPos(lg,v2);
		if(M>=0&&N>=0){
			lg.vex[M].vexl.push_back(N);
		    lg.vex[N].in++; 
		}	    
	}
}
bool TopoSort(LGraph&lg){
	int n=lg.vex.size();
    vector<int>in_copy;
	int i;
	for(i=0;i<n;i++){    //复制一份in,方便后期修改 
		in_copy.push_back(lg.vex[i].in);
	}
	queue<int> q;//用来临时存放 入度为0且没被删除的点
	
	for(i=0;i<n;i++){//先压入入度为0的点 
		if(in_copy[i]==0)
		    q.push(i);	    
	}
	//进行拓扑排序 
    while(!q.empty()){
		i=q.front();
		lg.topo.push_back(i); 
		list<int>::iterator it=lg.vex[i].vexl.begin();
		while(it!=lg.vex[i].vexl.end()){		
			in_copy[*it]--; 
			if(in_copy[*it]==0)
			    q.push(*it);
			it++;
		}
		q.pop();	
	} 	
	
	return  lg.topo.size() == n;;
}



int main(){
	int t;
	cin>>t;
	while(t--){
		int n,k,i;//n表示顶点数,k表示弧数 
		cin>>n>>k;
		LGraph lg(n);
		creatLGraph(lg,n,k);
		if(TopoSort(lg)){			                  
            for(i=0;i<lg.topo.size();i++){
               cout << lg.vex[lg.topo[i]].vexc<<" ";  // 输出顶点字符    
            }
            cout<<endl;
    
		}
		else
		     cout << "图中存在环，无法进行拓扑排序"<<endl;
	}
	
	return 0;
}

输入输出如下：

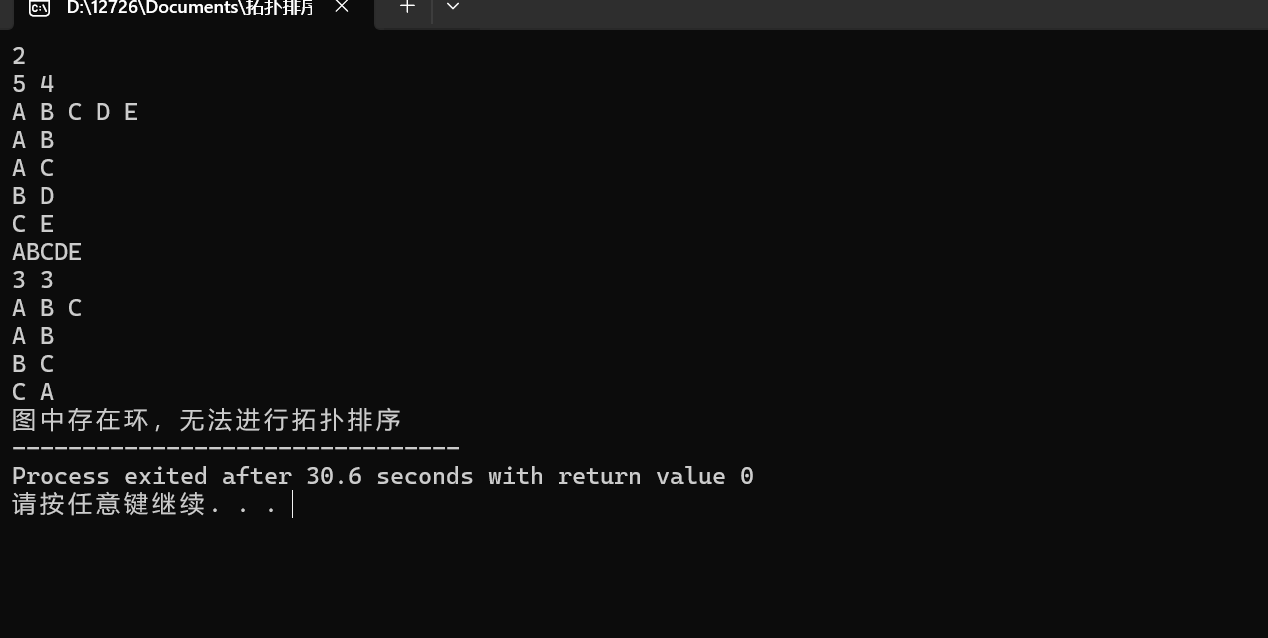
2、关键路径算法：

（1）AOE网（Activity On Edge Network):表示工程的有向图中用顶点表示活动，用弧表示活动之间的优先顺序，同时边上带权值的网。

（2）源点：入度为0的点；

汇点：出度为0的点；

（3）关键路径：从源点到汇点具有最大长度的路径

（4）算法实现原理：这里需要引入两参数：事件的最早发生时间etv和最晚发生时间ltv

最早发生时间即表示最快能在什么时候发生

最晚发生时间即最晚需要在什么时候发生，超过这个时间就延误整个工期

最早发生时间和最晚发生时间相同的事件称为关键活动，

由关键活动组成的路径即为关键路径

所以整个算法的关键就是求最早发生时间etv和最晚发生时间ltv！

代码及其注释如下：

#include<iostream>
#include<vector>
#include<list>
#include<queue>
using namespace std;
struct nextvex{   //用该结构体来表示与顶点相连接的点，包含该点的下标和两点间的权值 
	int vexi;   //表示下标
	int weight; //表示权值 
	nextvex(int v,int w):vexi(v),weight(w){
	} 
};            
struct vertex{
	int in=0;//这里添加一个int表示入度 
	char vexc;//表示顶点字符 
	list<nextvex>vexl;
};
struct LGraph{   //LGraph表示邻接表构成的图(list) 
	vector<vertex>vex;
	vector<int>etv;//事件最早发生时间数组 
	vector<int>ltv;//事件最晚发生时间数组 
	vector<int>topo;//拓扑排序序列 
	LGraph(int n){
		vex.resize(n);	
		etv.resize(n);
		ltv.resize(n);	
		int i;
		for(i=0;i<n;i++){
			etv[i]=0;
			ltv[i]=0x7FFFFFFF;
		}
	}
}; 
int findPos(LGraph lg,char vn){
	int n=lg.vex.size();
	int i;
	for(i=0;i<n;i++){
		if(lg.vex[i].vexc==vn)
		    return i;
	}
	return -1;
}
bool getEtvAndLtv(LGraph& lg){//获取 事件最早和最晚发生时间数组 
	int n=lg.vex.size();	
	int i,j; 
	vector<int>in_copy;
	for(i=0;i<n;i++){    //复制一份in,方便后期修改 
		in_copy.push_back(lg.vex[i].in);
	}
	
	queue<int> q;//用来临时存放 入度为0且没被删除的点
	for(i=0;i<n;i++){      //找到源点 
		if(in_copy[i]==0){
			q.push(i);
		}
	}
	//这里先进行拓扑排序并求得 事件最早发生时间
	while(!q.empty()){
		i=q.front();
		lg.topo.push_back(i); 
		list<nextvex>::iterator it=lg.vex[i].vexl.begin();
		while(it!=lg.vex[i].vexl.end()){
			if(lg.etv[it->vexi]<(lg.etv[i]+it->weight)){
				lg.etv[it->vexi]=(lg.etv[i]+it->weight);
			}
			in_copy[it->vexi]--; 
			if(in_copy[it->vexi]==0)
			    q.push(it->vexi);
			it++;
		}
		q.pop();
		
	} 	
	
	if(lg.topo.size()<n){
		cout << "图中存在环，无法计算etv" << endl;
		return false;
	}
	
    lg.ltv[lg.topo[n-1]]=lg.etv[lg.topo[n-1]];
    for(i=n-2;i>=0;i--){
    	list<nextvex>::iterator it=lg.vex[i].vexl.begin();
    	while(it!=lg.vex[i].vexl.end()){
			if(lg.ltv[i]>(lg.ltv[it->vexi]-it->weight)){
				lg.ltv[i]=(lg.ltv[it->vexi]-it->weight);
			}
			 
			it++;
		}	//cout<<"ggg";
	}

	
	return true;
}

void creatLGraph(LGraph& lg,int n,int k){
	int i;
	for(i=0;i<n;i++){
		cin>>lg.vex[i].vexc;
	}
	for(i=0;i<k;i++){
		char v1,v2;
		int w;
		cin>>v1>>v2>>w;
		int M=findPos(lg,v1);
		int N=findPos(lg,v2);
		if(M>=0&&N>=0){
			lg.vex[M].vexl.push_back(nextvex(N,w));
		    lg.vex[N].in++; 
		}	    
	}
	getEtvAndLtv(lg); 
}
void getCrucialWay(const LGraph&lg){
	int n=lg.vex.size();	
	int i; 
	queue<int> way;
	for(i=0;i<n;i++){
		if(lg.etv[i]==lg.ltv[i]){
			way.push(i);
		}
	}
	while(!way.empty()){
		cout<<lg.vex[way.front()].vexc<<" ";
		way.pop(); 
	}
	cout<<endl;
}



int main(){
	int t;
	cin>>t;
	while(t--){
		int n,k;//n表示顶点数,k表示弧数 
		cin>>n>>k;
		LGraph lg(n);
		creatLGraph(lg,n,k);
		int i;
		for(i=0;i<n;i++){
			cout<<lg.etv[i]<<" ";
			
		} 
		cout<<endl; 
		for(i=0;i<n;i++){
			cout<<lg.ltv[i]<<" ";
		} 
		cout<<endl;
		getCrucialWay(lg);
	}
	
	return 0;
}

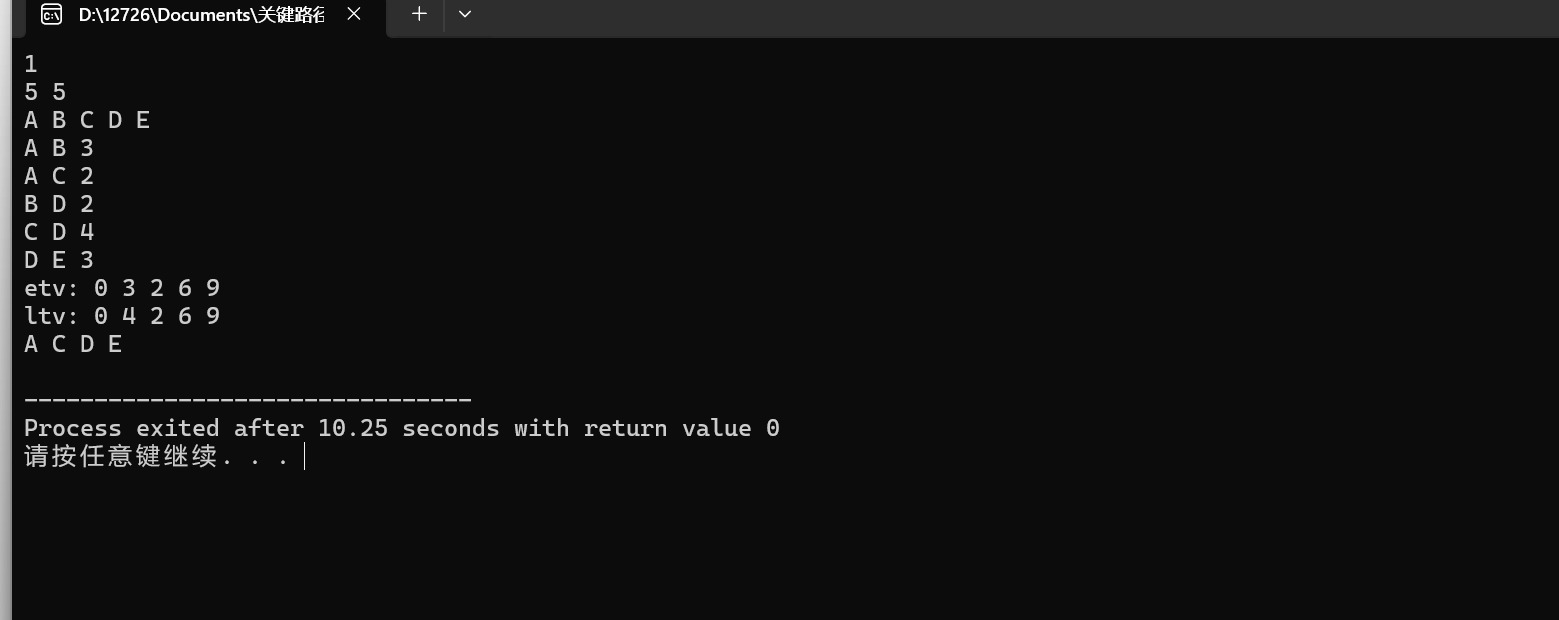
输入输出如下：