(动态规划)最长上升子序列

 

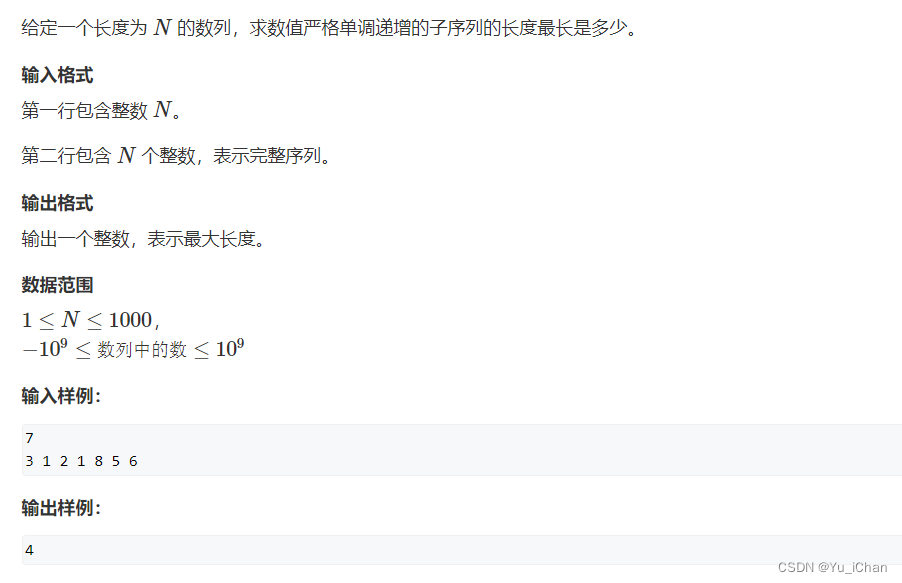
子序列的概念不同于子串，子序列可以不是连在一起的序列，一需要是在按主序列中的排序就行了

同样我们动态规划分为状态表示和状态计算

1.状态表示：f[i]表示从第一个数字开始算，以w[i]结尾的最大的上升序列。(以w[i]结尾的所有上升序列中属性为最大值的那一个)

2.状态计算（集合划分）：j∈(0,1,2,..,i-1), 在w[i] > w[j]时，
f[i] = max(f[i], f[j] + 1)。
有一个边界，若前面没有比i小的，f[i]为1（自己为结尾）。

3.最后在找f[i]的最大值。

代码如下

#include<iostream>
using namespace std;

const int N=1010;

int f[N],w[N];//f[i]表示以a[i]结尾的最大上升子序列
int n;

int main()
{
    cin>>n;
    for(int i=0;i<n;i++)scanf("%d",&w[i]);
    
    for(int i=0;i<n;i++)
    {
        f[i]=1;
        for(int j=0;j<i;j++)
        {
            if(w[j]<w[i])f[i]=max(f[i],f[j]+1);
        }
    }
    int res=0;
    for(int i=0;i<n;i++)res=max(res,f[i]);
    cout<<res<<endl;
    return 0;
}